Korelacija
V statistiki in teoriji verjetnosti korelacija pomeni, kako tesno sta povezana dva niza podatkov.
Povezanost ne pomeni vedno, da eno povzroča drugo. Zelo možno je, da je vpleten še tretji dejavnik.
Korelacija ima običajno eno od dveh smeri. Te so pozitivne ali negativne. Če je pozitivna, se oba sklopa skupaj povečata. Če je negativna, se en sklop povečuje, drugi pa zmanjšuje.
Za različne primere se uporablja veliko različnih meritev korelacije. Na primer, na grafu razpršitve ljudje narišejo črto najboljšega ujemanja, da pokažejo smer korelacije.
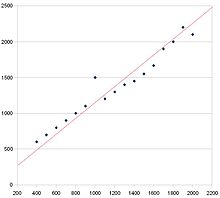
Ta razpršeni graf ima pozitivno korelacijo. To lahko ugotovite, ker je trend usmerjen navzgor in desno. Rdeča črta je črta najboljšega ujemanja.
Razlaga korelacije
Močna in šibka sta besedi, s katerima opisujemo korelacijo. Če je korelacija močna, so vse točke blizu skupaj. Če je korelacija šibka, so točke razporejene narazen. Obstajajo načini, kako s številkami prikazati, kako močna je korelacija. Te meritve se imenujejo korelacijski koeficienti. Najbolj znan je Pearsonov korelacijski koeficient produkt-moment. Podatke vnesete v formulo, ki vam da številko. Če je število 1 ali -1, potem je korelacija močna. Če je odgovor 0, korelacije ni. Druga vrsta korelacijskega koeficienta je Spearmanov korelacijski koeficient ranga.
Korelacija proti vzročnosti
Povezanost ne pomeni vedno, da ena stvar povzroča drugo stvar (vzročnost), saj je lahko oboje povzročilo kaj drugega. Na primer, v vročih dneh ljudje kupujejo sladoled, obenem pa hodijo na plažo, kjer nekatere pojedo morski psi. Med prodajo sladoleda in napadi morskih psov obstaja korelacija (v tem primeru se oboje zvišuje z naraščanjem temperature). Vendar to, da se prodaja sladoleda poveča, še ne pomeni, da prodaja sladoleda povzroča več napadov morskih psov ali obratno.
Ker korelacija ne pomeni vzročne zveze, znanstveniki, ekonomisti itd. preizkušajo svoje teorije z ustvarjanjem izoliranih okolij, v katerih se spreminja samo en dejavnik (če je to mogoče). Vendar pa politiki, prodajalci, novinarji in drugi pogosto namigujejo, da določena korelacija pomeni vzročno zvezo. To je lahko posledica neznanja ali želje po prepričevanju. Tako lahko novica pritegne pozornost z navedbo, da imajo ljudje, ki pogosteje uživajo določen izdelek, določene zdravstvene težave, kar pomeni vzročno zvezo, ki je lahko v resnici posledica nečesa drugega.
Sorodne strani
- Cohen, J., Cohen P., West, S.G., & Aiken, L.S. (2003). Applied multiple regression/correlation analysis for the behavioral sciences (Uporabna večkratna regresijska/korelacijska analiza za vedenjske vede). (Hillsdale, NJ: Lawrence Erlbaum Associates.
Vprašanja in odgovori
V: Kaj je korelacija?
O: Korelacija je način, kako tesno sta povezana dva niza podatkov.
V: Ali korelacija pomeni, da en niz podatkov povzroča drugega?
O: Ne, korelacija ne pomeni vedno, da en niz podatkov povzroča drugega. Dejansko je pogosto vpleten še tretji dejavnik.
V: Kateri sta dve smeri korelacije?
O: Dve smeri korelacije sta pozitivna in negativna.
V: Kaj pomeni pozitivna korelacija?
O: Pozitivna korelacija pomeni, da se oba niza podatkov skupaj povečujeta.
V: Kaj pomeni negativna korelacija?
O: Negativna korelacija pomeni, da en niz podatkov narašča, medtem ko drugi pada.
V: Ali obstajajo različne meritve korelacije?
O: Da, v različnih situacijah se uporablja veliko različnih meritev korelacije.
V: Kako ljudje pogosto prikažejo smer korelacije na grafu razpršitve?
O: Za prikaz smeri korelacije na grafu razpršitve ljudje pogosto narišejo črto najboljšega ujemanja.
