Moment sile (fizika): definicija, formula, enote in primeri
Definicija
V fiziki je moment sile (pogosto zgolj moment ali torque) merilo za težnjo sile, da povzroči vrtenje telesa okoli določene točke ali osi. Moment opisuje, kako močno in na kakšni razdalji od osi deluje sila — večja kot je sila ali daljša momentna roka, večji je učinek vrtenja.
Osnovna formula in razlaga
Za slučaj, ko sila deluje pravokotno na radij, velja preprosta zveza:
Moment = sila × pravokotna razdalja {\displaystyle {\text{Moment}}={\text{Sila}}\times {\text{Perendicular distance}}} 
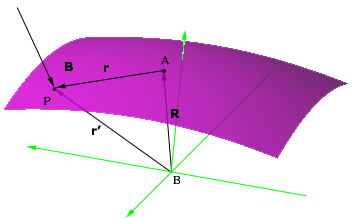
V vektorskem zapisu je moment sile glede na točko definiran kot vektorski produkt položajnega vektorja r in sile F:
M = r × F
Magnituda tega vektorja je:
|M| = r·F·sin(θ),
kjer je θ kot med vektorjema r in F. Če sila ni pravokotna na radij, uporabimo komponento sile, ki je pravokotna na radij, ali pravokotno razdaljo (momentno roko) d = r·sin(θ), tako da M = F·d.
Momenta roka (vzvod) in primeri
Pomembna veličina pri momentu je momentna roka (leva roka, lever arm) — najkrajša pravokotna razdalja med položajnim vektorjem in smerjo delovanja sile. Učinek lahko povečamo z daljšo momentno roko; to načelo uporabljajo preprosti stroji, na primer Vzvod, jermenica, zobnik in drugi, ki s spreminjanjem momentne roke ustvarjajo mehansko prednost s.
- Odpiranje vrat s pritiskom na kljuko: sila na robu vrat ustvari večji moment kot enaka sila bližje tečajem.
- Uporaba ključa (kroga) za privijanje vijaka: daljši ključ pomeni večji moment pri enaki sili.
- Gugalnica ali kolebnica: otroka uravnotežimo z različno oddaljenostjo od središča.
- Motorji in menjalniki producirajo navora (torque), kar je praktičen izraz za moment sile okoli osi vrtenja.
Enote in dimenzije
Enota v SI za moment je newton meter (N·m), kar je enako kg·m²·s⁻² (kg·m²/s²). Pomembno je poudariti, da čeprav ima N·m enake dimenzije kot džul (J = N·m), gre za različno fizično količino: džul meri energijo (skalarni), moment pa je vektorska količina (ima smer in lahko povzroča vrtenje).
Ravnovesje in smerni konvenciji
Načelo momenta v statiki: sistem je v rotacijskem ravnovesju, če je vsota vseh momentov glede na izbrano točko ali os enaka nič (ΣM = 0). Pogost način računanja je razdelitev momentov na smeri v smeri urinega kazalca in nasprotno; pri ravnovesju so te vsote enake:
vsota momentov v smeri urinega kazalca = vsota momentov v nasprotni smeri
Smer momenta določi pravilno ročno pravilo (right-hand rule): če zavrtimo prste v smeri delovanja momenta, kazalec palca kaže vektor momenta. V praksi se pogosto uporablja dogovor, da je moment, ki poskuša zavrteti v smeri urinega kazalca, negativen, v nasprotni smeri pa pozitiven (ali obratno — odvisno od izbrane konvencije; pomembno je biti dosleden).
Posebne situacije in dodatni pojmi
- Moment sile kot par sil (couple): par enakih in nasprotno usmerjenih sil, medsebojno premaknjenih, nima rezultantne sile, ima pa neto moment. Ta moment je enak produktu ene sile in razmika med silama.
- Bending moment: pri analizah nosilcev (beam) se uporablja pojem upogibnega momenta, ki vpliva na notranje napetosti in deformacije.
- Moment in moment vztrajnosti: nista enaka pojma — moment sile opisuje vpliv sile na vrtenje, moment vztrajnosti pa opisuje, kako telo odpira vrtenju glede na svojo maso (analogen masi pri pospešku).
Praktičen izračun — primer
Vzemimo ključ dolžine 0,30 m, na katerega deluje sila 50 N pravokotno na ključ. Moment je:
M = F × r = 50 N × 0,30 m = 15 N·m.
Če sila ne deluje pravokotno, recimo pod kotom 60° glede na radij, uporabimo komponento sile ali sin(θ):
|M| = r·F·sin(60°) = 0,30·50·(√3/2) ≈ 12,99 N·m.
Zaključek
Moment sile je temeljni koncept v mehaniki in inženirstvu, saj pove, kako sile povzročajo oziroma preprečujejo vrtenje. Razumevanje momentne roke, pravilnega izračuna (vključno z vektorskim produktom) in enot je ključnega pomena pri reševanju nalog iz statike, dizajnu orodij in strojev ter pri analizah konstrukcij.
Originalni primeri in ilustracije: vzvodi, odpiranje in zapiranje vrat, lomilke za orehe, odpirač za pločevinke in drugi preprosti stroji so vsakodnevne aplikacije principa momenta.
Zgodovina trenutka
Načelo momentov izhaja iz Arhimedovega odkritja načela delovanja vzvoda. V vzvodu deluje sila, v njegovem času najpogosteje človeška mišica, na roko, nekakšen nosilec. Arhimed je ugotovil, da je velikost sile, ki deluje na predmet, moment sile, definiran kot M = rF, kjer je F uporabljena sila, r pa je razdalja od uporabljene sile do predmeta.
Vprašanja in odgovori
V: Kaj je trenutek sile?
O: Moment sile, pogosto imenovan samo moment, je merilo težnje sile, da povzroči vrtenje predmeta okoli določene točke ali osi.
V: Kakšno vlogo ima pri tem konceptu momentna roka?
O: Momentna roka je razdalja od osi vrtenja in ima pri tem konceptu pomembno vlogo. Enostavni stroji, kot so vzvodi, jermenice in zobniki, ustvarjajo mehansko prednost s spreminjanjem momentne roke.
V: Katera je enota SI za momente?
O: Enota SI za momente je newton meter (kgm²/s²).
V: Kakšna je formula za izračun momentov?
O: Formula za izračun momentov je Moment = sila × pravokotna razdalja.
V: Katero načelo velja pri obravnavi momentov?
O: Momentno načelo pravi, da mora biti v primeru, ko je sistem v ravnovesju, vsota njegovih momentov v smeri urnega kazalca enaka vsoti njegovih momentov v nasprotni smeri urnega kazalca.
V: Kje so primeri uporabe momentov?
O: Primeri, kjer se uporabljajo momenti (učinek vrtenja), vključujejo vzvode, kot so gugalnice, odpiranje in zapiranje vrat, lomilke za matice, odpirač za pločevinke in lomilke.
V: Kako delujejo vzvodi glede na sile in razdalje?
O: Vzvod deluje tako, da ena sila, imenovana sila, premaga drugo silo, imenovano breme. V fiziki trenutek združuje fizikalno količino in razdaljo.
