Snellov zakon (lomni zakon) v optiki – definicija, formula in lomni količnik
Snellov zakon (lomni zakon) v optiki: definicija, formula, lomni količnik, izračuni in Fermatovo načelo za jasen vpogled v prehod svetlobe med mediji
Snellov zakon o lomu je znanstveni zakon o lomu svetlobe ali drugih valov. V optiki se Snellov zakon nanaša na hitrost svetlobe v različnih medijih. Zakon pravi, da se pri prehodu svetlobe skozi različne materiale (na primer iz zraka v steklo) razmerje sinusov vpadnega (vhodnega) in lomnega (izhodnega) kota ne spremeni:
sin θ 1 sin θ 2 = v 1 v 2 = n 2 n 1 {\displaystyle {\frac {\sin \theta _{1}}{\sin \theta _{2}}}={\frac {v_{1}}{v_{2}}}={\frac {n_{2}}{n_{1}}}} 
Vsak θ {\displaystyle \theta }
je kot, merjen od normale meje, v {\displaystyle v}
je hitrost svetlobe v ustreznem mediju (enote SI so metri na sekundo ali m/s). n {\displaystyle n}
je lomni količnik medija.
Lomni količnik vakuuma je 1, hitrost svetlobe v vakuumu pa je c {\displaystyle c}
. Ko valovanje prehaja skozi snov, katere lomni količnik je n, postane hitrost valovanja c n {\displaystyle {\frac {c}{n}}}. 
.
Snellov zakon je mogoče dokazati s Fermatovim načelom. Fermatovo načelo pravi, da svetloba potuje po poti, za katero potrebuje najmanj časa.
Razlaga in izpeljava
Razmerje v Snellovem zakonu povezuje kote z lastnostmi medijev. V bolj razumljivi obliki pogosto zapišemo:
sin θ1 / sin θ2 = n2 / n1
kjer je n = c / v. To pomeni, da večji lomni količnik (n) pomeni manjšo hitrost svetlobe v materialu in posledično večji odmik od prvotne smeri glede na normalo pri prehodu iz medija z manjšim n v medij z večjim n.
Kritični kot in popolni notranji odboj
Če svetloba prehaja iz gostejšega v redkejši medij (n1 > n2), obstaja kot vpadanja, pri katerem postane kot loma θ2 = 90°. Ta kot imenujemo kritični kot θc in ga izračunamo iz Snellovega zakona:
sin θc = n2 / n1
Za kote vpadanja večje od θc nastopi popolni notranji odboj — svetloba se ne prenaša v zunanji medij, temveč se popolnoma odbije nazaj v notranji medij. Ta pojav je osnova za delovanje optičnih vlaken in nekaterih prispevkov pri optičnih napravah.
Odvisnost od valovne dolžine (disperzija)
Lomni količnik n običajno ni konstanta za vse valovne dolžine — gre za funkcijo n(λ). Ta disperzija pomeni, da se različne barve (valovne dolžine) svetlobe lomijo pod malo različnimi koti, kar povzroči npr. razpad belega svetlobnega snopa na barve v prizmi.
Vektorska oblika in smeri
Snellov zakon je mogoče izraziti tudi s pomočjo vektorjev hitrosti ali valovnih vektorjev, kar je uporabno pri obravnavi kompleksnih meja in anizotropnih materialov. Pri enostavnih izračunih pa navadno zadostuje skalarna oblika s koti merjenimi od normale.
Uporabe in praktični primeri
- Optična stekla in leče — načrtovanje prelomnih lastnosti za fokusiranje svetlobe.
- Prizme — razpršitev svetlobe zaradi disperzije in različnih lomnih količnikov.
- Optična vlakna — izkoriščanje popolnega notranjega odboja za prenos signala na velike razdalje.
- Podvodna optika — izračun kota, pod katerim opazujemo objekte pod vodo glede na položaj opazovalca nad gladino.
Hitri primer izračuna
Če svetloba prehaja iz zraka (n1 ≈ 1,00) v steklo (n2 ≈ 1,50) in je vpadni kot θ1 = 30°, izračunamo lomni kot θ2 iz:
sin θ2 = (n1 / n2) · sin θ1 = (1,00 / 1,50) · sin 30° = (2/3) · 0,5 = 1/3
θ2 ≈ arcsin(1/3) ≈ 19,47°.
Opombe in omejitve
- Snellov zakon velja za linearne, homogenne in izotropne medije brez močnih disperzivnih ali nelinearnih učinkov. Pri zelo tankih plasteh ali frekvenčno odvisnih materialih je treba uporabiti naprednejše modele.
- Pri frekvencah, kjer snov močno absorbira, uporabljamo kompleksni lomni količnik n = n' + iκ, kar vpliva tudi na jakost in fazo prehajajočega vala.
Snellov zakon je zato temeljni pojav v optiki, ki povezuje geometrijo poti svetlobe z materialnimi lastnostmi in ima številne praktične uporabe, od vsakdanjih optičnih pripomočkov do naprednih telekomunikacijskih sistemov.
Svetlobni žarek pade na stekleno prizmo in se lomi
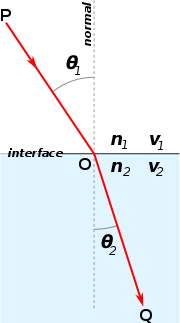
Lom svetlobe na meji med medijema z različnima lomnima količnikoma, pri čemer je n2 > n1
Zgodovina
Ta zamisel ima dolgo zgodovino. S problemom so se ukvarjali Hero iz Aleksandrije, Ptolemaj, Ibn Sahl in Huygens. Ibn Sahl je dejansko odkril zakon o lomu. Huygens je v delu Traité de la Lumiere iz leta 1678 pokazal, kako je mogoče Snellov sinusni zakon razložiti z valovno naravo svetlobe ali ga iz nje izpeljati.
Vprašanja in odgovori
V: Kaj je Snellov zakon o lomu?
O: Snellov zakon o lomu je znanstveni zakon o lomu svetlobe ali drugih valov. V optiki pravi, da se pri prehodu svetlobe skozi različne materiale razmerje med sinusoma vpadnega in lomnega kota ne spremeni.
V: Kako lahko dokažemo Snellov zakon?
O: Snellov zakon lahko dokažemo s Fermatovim načelom, ki pravi, da svetloba potuje po poti, ki traja najmanj časa.
V: Kaj je Fermatovo načelo?
O: Fermatovo načelo pravi, da svetloba potuje po poti, za katero potrebuje najmanj časa.
V: Kaj sta n in v v Snellovem zakonu?
O: n je lomni količnik medija, v pa je hitrost svetlobe v tem mediju (merjena v metrih na sekundo).
V: Kaj pomeni c v Snellovem zakonu?
O: c predstavlja hitrost svetlobe v vakuumu, ki ima lomni količnik enak 1.
V: Kako izračunate hitrost, ko valovanje prehaja skozi snov z lomnim količnikom n?
O: Ko valovanje prehaja skozi snov z lomnim količnikom n, postane hitrost c/n.
Iskati