Theorema egregium
Gaussova Egregijeva teorematika (latinsko Theorema Egregium) je pomemben rezultat diferencialne geometrije, ki ga je dokazal Carl Friedrich Gauss. Izrek se nanaša na ukrivljenost površin. Izrek pravi, da lahko ukrivljenost določimo samo z merjenjem kotov, razdalj in njihovih stopenj na površini. Ni treba govoriti o posebnem načinu, kako je površina vpeta v okoliški tridimenzionalni evklidski prostor. Z drugimi besedami, Gaussova ukrivljenost površine se ne spremeni, če površino upognemo, ne da bi jo raztegnili.
Gauss je trditev predstavil na ta način (prevedeno iz latinščine):
Zaradi tega formula iz prejšnjega članka sama vodi do izjemnega izreka. Če ukrivljeno površino razvijemo na kateri koli drugi površini, ostane mera ukrivljenosti v vsaki točki nespremenjena.
Izrek je "izjemen", ker izhodiščna definicija Gaussove ukrivljenosti neposredno uporablja položaj površine v prostoru. Zato je precej presenetljivo, da rezultat ni odvisen od njenega vgraviranja kljub vsem upogibnim in ukrivljenim deformacijam, ki jih je deležna.
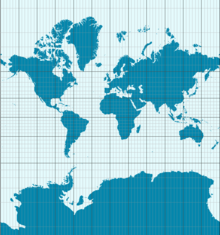
Posledica teoreme Egregium je, da Zemlje ni mogoče prikazati na zemljevidu brez popačenja. Mercatorjeva projekcija, prikazana na sliki, ohranja kote, vendar spreminja površino. Na primer, Antarktika je prikazana veliko večja, kot je v resnici.
Vprašanja in odgovori
V: Kaj je Gaussova Theorema Egregium?
O: Gaussova Egregijeva teorija je pomemben rezultat diferencialne geometrije o ukrivljenosti površin, ki ga je dokazal Carl Friedrich Gauss.
V: Kako lahko v skladu z Gaussovo teorijo Egregium določimo ukrivljenost?
O: V skladu z Gaussovo teorijo Egregium lahko ukrivljenost določimo samo z merjenjem kotov, razdalj in njihovih stopenj na površini.
V: Ali je za določitev ukrivljenosti potrebno govoriti o posebnem načinu vpetosti površine v okoliški tridimenzionalni evklidski prostor?
O: Ne, za določitev ukrivljenosti v skladu z Gaussovo Theorema Egregium ni treba govoriti o posebnem načinu vpetosti površine v okoliški tridimenzionalni evklidski prostor.
V: Ali se Gaussova ukrivljenost površine spremeni, če površino upognemo, ne da bi jo raztegnili?
O: Ne, Gaussova ukrivljenost površine se ne spremeni, če površino upognemo, ne da bi jo raztegnili v skladu z Gaussovo Egregijevo teorijo.
V: Kdo je predstavil ta izrek na tak način?
O: Gauss je predstavil teorem na ta način.
V: V čem je izrek izjemen?
O: Izrek je "izjemen", ker izhodiščna definicija Gaussove ukrivljenosti neposredno uporablja položaj površine v prostoru. Zato je precej presenetljivo, da rezultat ni odvisen od njenega vgraviranja kljub vsem upogibnim in ukrivljenim deformacijam, ki so bile izvedene.
V: Na kakšen način je Gauss predstavil izrek?
O: Gauss je izrek predstavil tako, da če ukrivljeno površino razvijemo na katero koli drugo površino, ostane mera ukrivljenosti v vsaki točki nespremenjena.
