Young-Laplaceova enačba
V fiziki je Young-Laplaceova enačba (/ləˈplɑːs/) nelinearna parcialna diferencialna enačba, ki opisuje razliko kapilarnega tlaka na meji med dvema statičnima tekočinama, kot sta voda in zrak. Ta razlika je posledica pojava površinske ali stenske napetosti. Stensko napetost lahko uporabimo le za zelo tanke stene. Young-Laplaceova enačba povezuje tlačno razliko z obliko površine ali stene. Je zelo pomembna pri preučevanju statičnih kapilarnih površin.
V fiziologiji je znan kot Laplaceov zakon. Uporablja se za opis tlaka v votlih organih.
Enačba je poimenovana po Thomasu Youngu, ki je leta 1805 razvil kvalitativno teorijo površinske napetosti, in Pierru-Simonu Laplaceu, ki je naslednje leto dokončal matematični opis. Včasih se imenuje tudi enačba Younga-Laplacea-Gaussa: Carl Friedrich Gauss je leta 1830 poenotil delo Younga in Laplacea. Gauss je diferencialno enačbo in robne pogoje izpeljal z uporabo načel virtualnega dela Johanna Bernoullija.
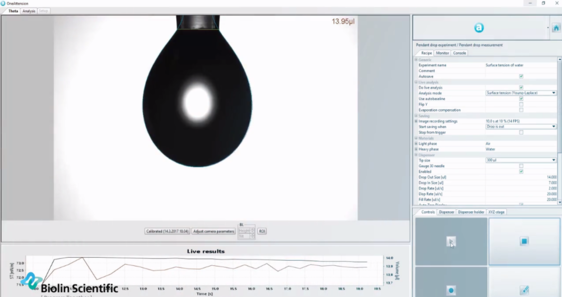
Optični tenziometri uporabljajo Youngovo-Laplaceovo enačbo za samodejno določanje površinske napetosti tekočine na podlagi oblike obeska kapljice.
Vprašanja in odgovori
V: Kaj je Young-Laplaceova enačba?
O: Young-Laplaceova enačba je nelinearna parcialna diferencialna enačba, ki opisuje razliko kapilarnega tlaka na meji med dvema statičnima tekočinama, kot sta voda in zrak.
V: Na kaj se nanaša?
O: Povezuje tlačno razliko z obliko površine ali stene.
V: Kdo je razvil to teorijo?
O: Teorijo je leta 1805 razvil Thomas Young, naslednje leto pa je njen matematični opis dokončal Pierre-Simon Laplace. Kasneje jo je leta 1830 poenotil Carl Friedrich Gauss.
V: Kako se uporablja v fiziologiji?
O: V fiziologiji je znan kot Laplaceov zakon in se uporablja za opis tlaka v votlih organih.
V: Kateri pojav pojasnjuje?
O: Young-Laplaceova enačba pojasnjuje pojav površinske ali stenske napetosti.
V: Ali stenska napetost velja za debele stene? O: Ne, stenska napetost se lahko uporablja le za zelo tanke stene.
