Prilagajanje krivulje
Prilagajanje krivulje je konstruiranje matematične funkcije, ki najbolje ustreza nizu podatkovnih točk.
Prilagajanje krivulje lahko vključuje interpolacijo ali glajenje. Interpolacija zahteva natančno prileganje podatkom. Pri glajenju se konstruira "gladka" funkcija, ki se približno prilega podatkom. Sorodna tema je regresijska analiza, ki se bolj osredotoča na vprašanja statističnega sklepanja, na primer koliko negotovosti je prisotne v krivulji, ki se prilega podatkom, opazovanim z naključnimi napakami.
Prilagojene krivulje lahko uporabimo za lažjo vizualizacijo podatkov, za ugibanje vrednosti funkcije, kadar ni na voljo podatkov, in za povzemanje odnosov med dvema ali več spremenljivkami. Ekstrapolacija se nanaša na uporabo prilagojene krivulje zunaj območja opazovanih podatkov. Pri tem je prisotna določena stopnja negotovosti, saj lahko odraža tako metodo, uporabljeno za konstruiranje krivulje, kot tudi opazovane podatke.
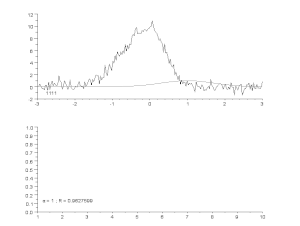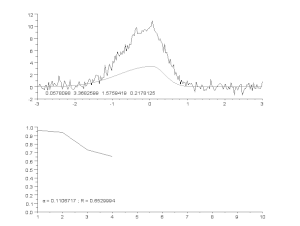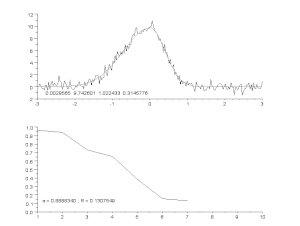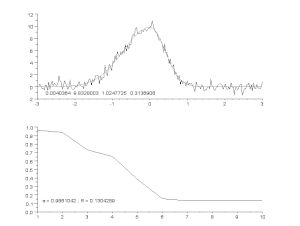
Prilagajanje hrupne krivulje z asimetričnim modelom vrha z iterativnim postopkom (Gauss-Newtonov algoritem s spremenljivim faktorjem dušenja α). Na vrhu: neobdelani podatki in model. Spodaj: razvoj normalizirane vsote kvadratov napak.
Vprašanja in odgovori
V: Kaj je prilagajanje krivulje?
O: Prilagajanje krivulje je postopek oblikovanja matematične funkcije, ki najbolje ustreza nizu podatkovnih točk.
V: Kateri sta dve vrsti prilagajanja krivulje?
O: Dve vrsti prilagajanja krivulje sta interpolacija in glajenje.
V: Kaj je interpolacija?
O: Interpolacija je vrsta prilagajanja krivulje, ki zahteva natančno prileganje podatkom.
V: Kaj je glajenje?
O: Glajenje je vrsta prilagajanja krivulje, ki konstruira "gladko" funkcijo, ki se približno prilega podatkom.
V: Kaj je regresijska analiza?
O: Regresijska analiza je sorodna tema, ki se osredotoča na vprašanja statističnega sklepanja, na primer koliko negotovosti je prisotne v krivulji, ki se prilega podatkom, opazovanim z naključnimi napakami.
V: Katere so nekatere uporabe prilegajočih se krivulj?
O: Prilagojene krivulje lahko uporabimo za lažjo vizualizacijo podatkov, ugibanje vrednosti funkcije, kadar ni podatkov, in povzemanje odnosov med dvema ali več spremenljivkami.
V: Kaj je ekstrapolacija?
O: Ekstrapolacija je uporaba prilagojene krivulje zunaj območja opazovanih podatkov. Vendar je to predmet določene negotovosti, saj lahko odraža tako metodo, uporabljeno za konstruiranje krivulje, kot tudi opazovane podatke.
