Funkcija v matematiki: definicija, domena, kodomena in primeri
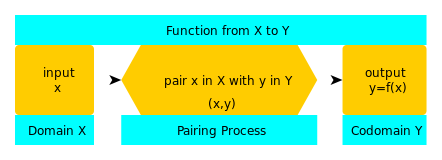
V matematiki je funkcija matematični objekt, ki vsakemu elementu iz neke množice (vhodu) priredi natanko en element iz druge množice (izhoda). Vhodi so pogosto števila, vektorji ali drugi objekti, izhodi pa so objekti iste ali druge vrste — bistvo pa je, da so parjenje vhoda in izhoda jasno določeni.
Funkcijo si lahko predstavljamo kot "stroj", ki sprejme vrednost x in vrne izhodno vrednost y. Množica vseh možnih vhodnih vrednosti se imenuje domena. Množica, znotraj katere ležijo vsi možni izhodi funkcije, se imenuje kodomen (ang. codomain). Pogosto se razlikuje med kodomenom in dejansko množico vrednosti, ki jih funkcija doseže — to zadnjo množico imenujemo vrednostna množica ali image (obseg).
Če za neko pravilo zapišemo, da iz x nastane y, pišemo, da je y funkcija x in zapišemo y = f(x). Črka f je ime funkcije. Pogosta simbolna oblika za funkcijo je:
f : X → Y {\displaystyle f:X\to Y} 
Ta zapis pomeni: f je funkcija, katere domena je X, kodomen pa Y. Puščica predstavlja pravilo, ki vsakemu elementu iz X priredi en element iz Y.
Preprost primer
Enostaven primer funkcije je f(x) = x + 1. Če kot vhod vzamemo naravna števila x {\displaystyle x}
(0, 1, 2, 3, ...), dobimo kot izhode naravna števila y {\displaystyle y} 
, kjer je y {\displaystyle y} + 1 — torej za vhod 0 je izhod 1, za vhod 1 je izhod 2 itd. Ta primer kaže osnovno lastnost funkcije: vsakemu vhodu je prirejen natanko en izhod.
Notacija in lastnosti
- Domena (X): množica vseh dovoljenih vhodov.
- Kodomen (Y): množica, v kateri naj bi bili izhodi; nekatere vrednosti iz kodomena morda niso dosežene.
- Vrednostna množica (image): dejanska množica izhodov f(X) = { f(x) : x ∈ X }.
- Enoličnost: za vsak x ∈ X obstaja natanko en y ∈ Y tak, da y = f(x).
Vrste funkcij (kratka razlaga)
- Injektivna (ena na ena): različni vhodi dajo različne izhode. Formalno: če f(x1)=f(x2), potem x1=x2.
- Surjektivna (na): za vsak y ∈ Y obstaja x ∈ X, da je f(x)=y; torej je image enak kodomenu.
- Bijektivna: funkcija, ki je hkrati injektivna in surjektiv; ima obratno funkcijo (inverz).
- Kompozicija funkcij: če sta f : X → Y in g : Y → Z, je (g ∘ f)(x) = g(f(x)). Kompozicija povezuje procese.
Primeri različnih funkcij
- f(x) = x^2 z domeno R (realnih števil) je funkcija, katere image je [0, ∞); ni injektivna na celotnih R (ker f(-1)=f(1)), vendar je surjektivna na [0, ∞).
- f(x) = 2x + 3 na R je bijektivna (ima inverz f^{-1}(y) = (y-3)/2).
- Absolutna vrednost g(x) = |x| je funkcija z domeno R in image [0, ∞); ni injektivna, razen če domeno omejimo na [0, ∞).
- Diskretna funkcija: npr. f: {a,b,c} → {1,2} s parjenji f(a)=1, f(b)=2, f(c)=1. Tu lahko jasno vidimo mapping med končnimi množicami.
- Delno definirane funkcije in členaste (piecewise) funkcije: funkcija je lahko definirana z različnimi obrazci na različnih delih domene, npr. f(x)=x^2 za x≤0 in f(x)=x+1 za x>0.
Graf funkcije
Graf funkcije f : R → R je množica točk v ravnini {(x, f(x)) : x ∈ R}. Graf daje vizualen prikaz obnašanja funkcije — npr. kjer raste, pada, kje ima maksimum ali minimum, asimptote in podobno.
Kaj funkcija ni
Funkcija ni le matematična formula; lahko je pravilo, tabela, račun ali celo zapleten algoritem, ki vsakemu vhodu priredi točno en izhod. Bistveno je pravilo parjenja, ne oblika zapisa.
Zaključek
Funkcija je temeljni koncept v matematiki, uporaben v skoraj vseh vejah (analiza, algebra, statistika, računalništvo). Razumevanje domene, kodomena, image in lastnosti (injektivnost, surjektivnost, bijektivnost) pomaga pri analizi in uporabi funkcij v praktičnih in teoretičnih primerih.
Metafore
Tabele
Vhode in izhode lahko vnesete v tabelo, kot je prikazana na sliki; to je enostavno, če ni preveč podatkov.
Grafi
Na sliki je razvidno, da sta 2 in 3 povezana s c; v drugo smer to ni dovoljeno, 2 ne bi mogla izvesti c in d, vsak vhod ima lahko le en izhod. Vsi f ( x ) {\displaystyle f(x)} 
(c in d na sliki) običajno imenujemo slikovna množica f {\displaystyle f}, 
slikovna množica pa je lahko celotna kodomena ali ne. Lahko rečemo, da je podmnožica A kodomena s slikovno množico f(A). Če imajo vhodi in izhodi določen vrstni red, jih je enostavno narisati na graf:
To bo omogočilo, da se 2 in 3 spari z ni dovoljeno v drugo smer, tudi med kodno domeno lahko naredimo sliko ali ne. Zaključimo lahko, da je podmnožica A kodomene slika množice F(A).
Zgodovina
Leta 1690 sta GottfriedLeibniz in Johann Bernoulli uporabila besedo funkcija v medsebojnih črkah, tako da se je sodobni koncept začel hkrati z računom.
Leta 1748 je Leonhard Euler podal: "Če so nekatere količine tako odvisne od drugih količin, da se ob spremembi slednjih spremenijo tudi prve, potem se prve količine imenujejo funkcije slednjih. Ta opredelitev velja precej široko in vključuje vse načine, na katere je mogoče eno količino določiti z drugo. Če torej x označuje spremenljivo količino, potem vse količine, ki so kakor koli odvisne od x ali jih ta določa, imenujemo funkcije x.", kar je zelo sodobno.
Dirichlet je običajno avtor različice, ki se je v šolah uporabljala do druge polovice 20. stoletja: "y je funkcija spremenljivke x, definirana na intervalu a < x < b, če vsaki vrednosti spremenljivke x na tem intervalu ustreza določena vrednost spremenljivke y. Prav tako ni pomembno, na kakšen način je to ujemanje ugotovljeno."
Leta 1939 je Bourbaki posplošil Dirichletovo definicijo in podal teoretično različico definicije množic kot korespondenco med vhodi in izhodi; ta se je v šolah uporabljala približno od leta 1960.
Leta 1970 je Bourbaki podal sodobno definicijo kot trojico f = ( X , Y , F ) {\displaystyle f=(X,Y,F)} 
s F ⊂ X × Y , ( x , f ( x ) ) ∈ F {\displaystyle F\podskupina X\časov Y,(x,f(x))\in F}
(tj. f : X → Y {\displaystyle f:X\v Y} in F = { ( x , f ( x ) ) | x ∈ X , f ( x ) ∈ Y } {\displaystyle F=\{(x,f(x))|x\in X,f(x)\in Y\}} 
).
Vrste funkcij
- Osnovne funkcije - funkcije, ki se jih običajno učimo v šoli: ulomki, kvadratni koreni, funkcije sinus, kosinus in tangens ter nekatere druge funkcije.
- Funkcije, ki niso osnovne - Večina jih ne uporablja operacij, ki se jih ne učimo v šoli (na primer + ali - ali moči). Mnogi integrali so neelementarni.
- Inverzne funkcije - funkcije, ki razveljavijo drugo funkcijo. Na primer: če je F(x) inverzna funkcija f(x)=y, potem je F(y)=x. Vse funkcije nimajo inverznih funkcij.
- Posebne funkcije: Funkcije, ki imajo imena. Na primer: sinus, kosinus in tangens. Funkcije, kot je f(x)=3x (trikrat x), se ne imenujejo posebne funkcije. Lahko so elementarne, neelementarne ali inverzne.
Vprašanja in odgovori
V: Kaj je funkcija v matematiki?
O: Funkcija v matematiki je objekt, ki ustvari izhod, ko dobi vhod, ki je lahko število, vektor ali karkoli, kar lahko obstaja znotraj množice stvari.
V: Kateri sta dve množici, povezani s funkcijami?
O: Množica vseh vrednosti, ki jih lahko ima x, se imenuje domena, množica, ki vsebuje vse vrednosti, ki jih lahko ima y, pa se imenuje sopomena.
V: Kako se pogosto označujejo funkcije?
O: Funkcije so pogosto označene s poševnimi črkami, kot so f, g, h.
V: Kako predstavimo funkcijo?
O: Funkcijo predstavimo tako, da zapišemo y = f(x), kjer je f ime funkcije, f : X → Y (funkcija iz X v Y) pa predstavlja tri dele funkcije - domeno (X), kodomeno (Y) in postopek parjenja (puščica).
V: Ali lahko navedete primer funkcije?
O: Primer funkcije je f(x) = x + 1. Na vhodu dobimo naravno število x in dobimo naravno število y, ki je x + 1. Če na primer damo 3 kot vhodni podatek za f, dobimo izhodno število 4.
V: Ali mora biti vsaka funkcija enačba?
O: Ne, ni nujno, da je vsaka funkcija enačba. Glavna ideja funkcij je, da se vhodi in izhodi nekako povežejo v par - tudi če je to morda zelo zapleteno.
