Vektor (matematika)

Primeri vektorjev

• John gre 20 metrov proti severu. Smer "sever" in razdalja "20 metrov" sta vektorja.
• Jabolko pade navzdol s hitrostjo 10 metrov na sekundo. Smer "navzdol" skupaj s hitrostjo "10 metrov na sekundo" je vektor. Tovrstni vektor imenujemo tudi hitrost.

Primeri skalarjev

• Razdalja med dvema krajema je 10 kilometrov. Ta razdalja ni vektor, ker ne vsebuje smeri.
• Število sadežev v škatli ni vektor.
• Oseba, ki kaže, ni vektor, ker ima samo smer. Ni velikosti (na primer razdalje od prsta osebe do stavbe).
• Dolžina predmeta.
• Avto vozi s hitrostjo 100 kilometrov na uro. To ni opis vektorja, saj je podana le velikost, ni pa podana smer.

Več primerov vektorjev

• Premik je vektor. Premik je razdalja, ki jo nekaj premakne v določeni smeri. Samo merilo razdalje je skalar.
• Sila, ki vključuje smer, je vektor.
• Hitrost je vektor, ker je to hitrost v določeni smeri.
• Pospešek je stopnja spremembe hitrosti. Predmet pospešuje, če spreminja hitrost ali smer.

Kako dodati vektorje

Dodajanje vektorjev na papir z metodo od glave do repa

Metoda seštevanja vektorjev od glave do repa je uporabna za oceno rezultata seštevanja dveh vektorjev na papirju. Naredimo jo tako:

• Vsak vektor je narisan kot puščica z določeno dolžino, pri čemer vsaka enota dolžine na papirju predstavlja določeno velikost vektorja.
• Narišite naslednji vektor z repom (koncem) drugega vektorja na glavi (spredaj) prvega vektorja.
• Ponovite za vse nadaljnje vektorje: Narišite rep naslednjega vektorja na glavo prejšnjega vektorja.
• Narišite črto od repa prvega vektorja do glave zadnjega vektorja - to je rezultanta (vsota) vseh vektorjev.

Imenuje se metoda "od glave do repa", ker vsaka glava prejšnjega vektorja vodi v rep naslednjega vektorja.

Uporaba obrazca komponente

^{[je treba pojasniti}

Uporaba oblike komponente za seštevanje dveh vektorjev dobesedno pomeni, da seštejemo komponente vektorjev in dobimo nov vektor. Na primer, naj bosta a in b dva dvodimenzionalna vektorja. Ta vektorja lahko zapišemo v obliki njunih komponent.

a = ( a x , a y ) {\displaystyle \mathbf {a} =(a_{x},a_{y})}

b = ( b x , b y ) {\displaystyle \mathbf {b} =(b_{x},b_{y})}

Predpostavimo, da je c vsota teh dveh vektorjev, tako da je c = a + b. To pomeni, da je c = ( a x + b x , a y + b y ) {\displaystyle \mathbf {c} =(a_{x}+b_{x},a_{y}+b_{y})} .

Tukaj je primer seštevanja dveh vektorjev z uporabo njunih komponentnih oblik.

a = ( , 3-1 ) {\displaystyle \mathbf {a} =(3,-1)}

b = ( ,2 ) 2{\displaystyle \mathbf {b} =(2,2)}

c = a + b {\displaystyle \mathbf {c} =\mathbf {a} +\mathbf {b} }

= ( a x + b x , a y + b y ) {\displaystyle =(a_{x}+b_{x},a_{y}+b_{y})}

= ( +3 , 2- 1+ ) 2{\displaystyle =(3+2,-1+2)}

= ( ,5 ) 1{\displaystyle =(5,1)}

Ta metoda deluje za vse vektorje, ne le za dvodimenzionalne.

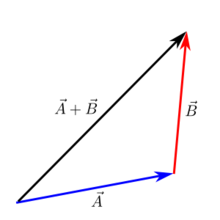
Dodatek od glave do repa

Kako pomnožiti vektorje

Uporaba točkovnega produkta

Ena od metod za množenje vektorjev je točkovni produkt. Rezultat je skalar. Uporablja obliko komponente:

a = ( ,2 ) 3b = ( ,1 )4 a ⋅ b = ( ,2 ) 3⋅ ( ,1 ) 4= ( 2⋅1 ) + (3 ⋅4 ) = +2 = 12{\displaystyle14 {\begin{aligned}\mathbf {a} =(2,3)\\\\mathbf {b} =(1,4)\\\mathbf {a} \cdot \mathbf {b} =(2,3)\cdot (1,4)\\=(2\cdot 1)+(3\cdot 4)\\=2+12=14\end{aligned}}

Uporaba navzkrižnega produkta

Križni produkt je še ena metoda za množenje vektorjev. Tako dobimo še en vektor. Uporaba oblike komponente:

a × b = | a | | b | sin ( θ ) n {\displaystyle \mathbf {a} \times \mathbf {b} =|\mathbf {a} ||\mathbf {b} |\sin(\theta )\mathbf {n} }

Tukaj | a | {\displaystyle |\mathbf {a} |} pomeni dolžino {\displaystyle \mathbf {a} } in n {\displaystyle \mathbf {n} } je enotski vektor pod pravim kotom na oba a {\displaystyle \mathbf {a} } in b {\displaystyle \mathbf {b} } .

Množenje s skalarjem

Če želite pomnožiti vektor s skalarjem (običajnim številom), pomnožite število z vsako komponento vektorja:

c x = ( c x , 1c x , 2... , c x n ) {\displaystyle c\,\mathbf {x} =(c\,x_{1},c\,x_{2},...,c\,x_{n})}

Primer tega je

c = x5 = ( ,3 ) 4c x = ( 5⋅3 , 5⋅4 ) = ( ,15 ) 20{\displaystyle {\begin{aligned}c=5\\\\mathbf {x} =(3,4)\\c\,\mathbf {x} =(5\cdot 3,5\cdot 4)\\=(15,20)\end{aligned}}}

Sorodne strani

• Vektorska grafika
• Vektorsko polje