AlegsaOnline.com

Matematika: definicija, področja in uporaba v znanosti in vsakdanjem življenju

Matematika definicija in področja, uporaba v znanosti in vsakdanjem življenju, jasne razlage številk, struktur, geometrije in analize, praktični primeri za študij in delo

Avtor: Leandro Alegsa

19-08-2025

Matematika je preučevanje številk, oblik in vzorcev. Beseda izhaja iz grške besede "μάθημα" (máthema), ki pomeni "znanost, znanje ali učenje", in se včasih skrajša na maths (v Angliji, Avstraliji, na Irskem in Novi Zelandiji) ali math (v Združenih državah Amerike in Kanadi). Učenci in njihove šole te kratke besede pogosto uporabljajo za aritmetiko, geometrijo ali preprosto algebro.

Matematika vključuje študij:

Številke: kako lahko stvari preštejemo.
Struktura: kako so stvari organizirane. To podpodročje se običajno imenuje algebra.
Kraj: kje so stvari in kako so razporejene. To podpodročje se običajno imenuje geometrija.
Sprememba: kako se stvari spremenijo. To podpodročje se običajno imenuje analiza.

Matematika je uporabna za reševanje problemov, ki se pojavljajo v resničnem svetu, zato jo poleg matematikov študirajo in uporabljajo tudi številni drugi ljudje. Danes je nekaj matematike potrebne pri številnih poklicih. Ljudje, ki delajo na področju poslovanja, znanosti, inženirstva in gradbeništva, potrebujejo nekaj znanja matematike.

Glavna področja matematike

Aritmetika — temeljno računanje s številkami: seštevanje, odštevanje, množenje in deljenje. Uporablja se pri vsakdanjih opravilih, kot so nakupi ali delo z denarjem.
Algebra — preučuje strukture, enačbe in operacije z neznankami; omogoča modeliranje problemov z izrazi in reševanje splošnih pravil (npr. linearne in kvadratne enačbe).
Geometrija — ukvarja se z oblikami, velikostmi, razmerji in položaji v prostoru; vključuje ravninsko geometrijo, trirazsežno geometrijo in analitično geometrijo (ko uporabljamo koordinate).
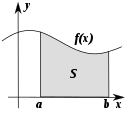
Analiza (diferencialni in integralni račun) — preučuje spremembe in gibanje; pojmi, kot so odvod in integral, so osnova za razumevanje hitrosti, pospeška in površin pod krivuljami.
Verjetnost in statistika — ukvarjata se z naključnostjo, zbiranjem, analizo in interpretacijo podatkov; ključni sta v raziskavah, medicini, ekonomiji in podatkovni znanosti.
Diskretna matematika — preučuje diskretne strukture, kot so grafi, množice in kombinatorika; osnova za računalniške algoritme in kriptografijo.
Numerične metode — tehnike za približno reševanje matematičnih problemov na računalniku, kjer analitične rešitve niso praktične.
Teoretična področja — npr. teorija števil, topologija, abstraktna algebra in logika, kjer se razvijajo abstraktne ideje, pogosto z globokimi povezavami v drugih vedah.

Metode in način dela v matematiki

Matematika temelji na natančni definiciji pojmov, logičnih sklepih in dokazih. Dokaz je argument, ki iz vnaprej sprejetih predpostavk in pravil logike izpelje resničnost neke trditve. Pomembna je tudi abstrakcija — poenostavljanje problema tako, da obdržimo samo bistvene lastnosti, in modeliranje, kjer resnične pojave opisujemo z matematičnimi enačbami.

Računska in simbolna notacija omogočata krajše in natančnejše izražanje mišljenja; algoritmi in računalniška orodja pa omogočajo reševanje velikih ali kompleksnih problemov.

Uporaba v znanosti in tehnologiji

V fiziki matematika opisuje gibanje, energijo in sile (Newtonova mehanika, Maxwellove enačbe, kvantna mehanika).
V inženirstvu se uporablja za načrtovanje konstrukcij, analizo obremenitev, optimizacijo in simulacije.
V računalništvu so ključne diskretna matematika, teorija grafov, teorija informacij in algoritmi; kriptografija temelji na številskih lastnostih in algebraičnih strukturah.
V biologiji in medicini matematični modeli opisujejo širjenje bolezni, biofizikalne procese in statistične analize kliničnih podatkov.
V ekonomiji in financah se matematika uporablja pri modeliranju trgov, ocenjevanju tveganj, statistični analizi in optimizaciji portfeljev.
V meteorologiji in okoljskih znanostih so numerične metode osnova za napovedovanje vremena in simulacije podnebnih sprememb.

Primeri uporabe v vsakdanjem življenju

Računanje stroškov, sestavljanje proračuna in obrestno računstvo pri posojilih ali varčevanju.
Merjenje površin in volumnov pri prenovi doma ali urejanju vrta.
Uporaba proporcij in razmerij pri kuhanju ali mešanju snovi.
Navigacija in GPS: geometrija in trigonometrija pomagata določati položaj in pot.
Analiza podatkov in statistika pri spremljanju zdravja, športnih rezultatov ali tržnih raziskavah.

Izobraževanje in pomen razvijanja matematičnega mišljenja

Matematika je del osnovnega izobraževanja, ker razvija sposobnosti logičnega mišljenja, reševanja problemov in natančnega izražanja. V šoli se začne z osnovno aritmetiko in geometrijo, nato sledi algebra, analiza in naprednejše teme na srednji šoli ter fakulturni stopnji.

Nasveti za učenje: razumevanje osnovnih pojmov je pomembnejše od mehaničnega pomnjenja; reševanje različnih nalog gradi intuicijo; iskanje vizualnih predstavitev in uporaba računalniških orodij (simulatorji, grafični kalkulatorji) lahko pospeši učenje.

Zaključek

Matematika je univerzalno orodje za opisovanje, razumevanje in reševanje problemov tako v znanosti kot v vsakdanjem življenju. Njena lepota je v kombinaciji abstraktne jasnoče in praktične uporabnosti: z istimi osnovnimi načeli lahko opisujemo zelo različne pojave — od preprostih računov pri nakupih do zapletenih modelov v naravoslovju in tehnologiji.

Reševanje problemov v matematiki

Matematika rešuje probleme z uporabo logike. Eno glavnih orodij logike, ki ga uporabljajo matematiki, je dedukcija. Dedukcija je poseben način razmišljanja, s katerim odkrivamo in dokazujemo nove resnice s pomočjo starih resnic. Za matematika je razlog, zakaj je nekaj resnično (imenovan dokaz), prav tako pomemben kot dejstvo, da je nekaj resnično, in ta razlog pogosto najde z dedukcijo. Uporaba dedukcije je tisto, po čemer se matematično razmišljanje razlikuje od drugih vrst znanstvenega razmišljanja, ki se lahko opira na poskuse ali razgovore.

Logiko in sklepanje matematiki uporabljajo za oblikovanje splošnih pravil, ki so pomemben del matematike. Ta pravila izpuščajo informacije, ki niso pomembne, tako da lahko eno samo pravilo pokriva veliko situacij. Z iskanjem splošnih pravil matematika hkrati rešuje številne probleme, saj se ta pravila lahko uporabijo pri drugih problemih. Ta pravila lahko imenujemo teorije (če so dokazana) ali domneve (če še ni znano, ali so resnična). Večina matematikov za iskanje logičnega dokaza uporablja nelogično in ustvarjalno razmišljanje.

Včasih matematika najde in preuči pravila ali ideje, ki jih še ne razumemo. V matematiki pogosto izberemo ideje in pravila, ker se nam zdijo preprosta ali elegantna. Po drugi strani pa včasih te ideje in pravila najdemo v resničnem svetu, potem ko jih preučimo v matematiki; to se je v preteklosti že večkrat zgodilo. Na splošno nam preučevanje pravil in idej v matematiki lahko pomaga bolje razumeti svet. Nekateri primeri matematičnih problemov so seštevanje, odštevanje, množenje, deljenje, računanje, ulomki in decimalke. Algebrske probleme rešujemo z vrednotenjem določenih spremenljivk. Kalkulator odgovori na vsak matematični problem s štirimi osnovnimi aritmetičnimi operacijami.

Področja študija matematike

Številka

Matematika vključuje preučevanje števil in količin.Je veja znanosti, ki se ukvarja z logiko oblike, količine in razporeditve. Večino spodaj naštetih področij preučujejo na različnih področjih matematike, vključno s teorijo množic in matematično logiko. Študij teorije števil se običajno bolj osredotoča na strukturo in obnašanje celih števil kot pa na dejanske temelje samih števil, zato ni naveden v tem podpoglavju.

0 , 1 , 2 , 3 , ... {\displaystyle 0,1,2,3,\ldots } $0,1,2,3,\ldots$	... , - 1 , 0 , 1 , ... {\displaystyle \ldots ,-1,0,1,\ldots } $\ldots ,-1,0,1,\ldots$	1 2 , 2 3 , 0,125 , ... {\displaystyle {\frac {1}{2}},{\frac {2}{3}},0,125,\ldots } ${\frac {1}{2}},{\frac {2}{3}},0.125,\ldots$	π , e , 2 , ... {\displaystyle \pi ,e,{\sqrt {2}},\ldots } $\pi ,e,{\sqrt {2}},\ldots$	1 + i , 2 e i π / 3 , ... {\displaystyle 1+i,2e^{i\pi /3},\ldots } $1+i,2e^{i\pi /3},\ldots$
Naravna števila	Celoštevilke	Racionalna števila	Realna števila	Kompleksna števila
0 , 1 , ... , ω , ω + 1 , ... , 2 ω , ... {\displaystyle 0,1,\ldots ,\omega ,\omega ,\omega +1,\ldots ,2\omega ,\ldots } $0,1,\ldots ,\omega ,\omega +1,\ldots ,2\omega ,\ldots$	ℵ 0 , ℵ 1 , ... {\displaystyle \aleph _{0},\aleph _{1},\ldots } $\aleph _{0},\aleph _{1},\ldots$	+ , - , × , ÷ {\displaystyle +,-,\times ,\div } $+,-,\times ,\div$	> , ≥ , = , ≤ , < {\displaystyle >,\geq ,=,\leq ,< } $>,\geq ,=,\leq ,<$	f ( x ) = x {\displaystyle f(x)={\sqrt {x}}} $f(x)={\sqrt {x}}$
Zaporedna števila	Kardinalne številke	Aritmetične operacije	Aritmetična razmerja	Funkcije

Struktura

Številna področja matematike preučujejo strukturo, ki jo ima predmet. Večina teh področij je del študija algebre.


Teorija števil	Abstraktna algebra	Linearna algebra	Teorija reda	Teorija grafov

Oblika

Nekatera področja matematike preučujejo oblike stvari. Večina teh področij je del študija geometrije.


Topologija	Geometrija	Trigonometrija	Diferencialna geometrija	Fraktalna geometrija

Sprememba

Nekatera področja matematike proučujejo način, kako se stvari spreminjajo. Večina teh področij je del študija analize.


Calculus	Vektorski račun	Analiza

Diferencialne enačbe	Dinamični sistemi	Teorija kaosa

Uporabna matematika

Uporabna matematika uporablja matematiko za reševanje problemov na drugih področjih, kot so inženirstvo, fizika in računalništvo.

Numerična analiza - Optimizacija - Teorija verjetnosti - Statistika - Matematične finance - Teorija iger - Matematična fizika - Fluidna dinamika - Računski algoritmi

Znane trditve

Te trditve so zanimale matematike in ljudi, ki niso matematiki.

Pitagorov izrek - Fermatov zadnji izrek - Goldbachova domneva - Domneva o dvojnem praštevilu - Gödelove trditve o nepopolnosti - Poincaréjeva domneva - Cantorjev diagonalni argument - Izrek o štirih barvah - Zornova lema - Eulerjeva identiteta - Church-Turingova teza

To so trditve in domneve, ki so močno spremenile matematiko.

Riemannova hipoteza - Hipoteza kontinuuma - P proti NP - Pitagorov izrek - Centralni limitni izrek - Temeljni izrek računa - Temeljni izrek algebre - Temeljni izrek aritmetike - Temeljni izrek projektivne geometrije - Klasifikacijski izreki površin - Gauss-Bonnetov izrek - Fermatov zadnji izrek - Kantorovičev izrek

Osnove in metode

Napredek v razumevanju narave matematike vpliva tudi na način, kako matematiki preučujejo svoj predmet.

Filozofija matematike - Matematični intuicionizem - Matematični konstruktivizem - Osnove matematike - Teorija množic - Simbolna logika - Teorija modelov - Teorija kategorij - Logika - Povratna matematika - Tabela matematičnih simbolov

Zgodovina in svet matematikov

Matematika v zgodovini in zgodovina matematike.

Zgodovina matematike - Časovnica matematike - Matematiki - Fieldsova medalja - Abelova nagrada - Nagrada tisočletja (Clay MathPrize) - Mednarodna matematična zveza - Matematična tekmovanja - Lateralno mišljenje - Matematika in spol

Nagrade na področju matematike

Nobelove nagrade za matematiko ni. Matematiki lahko za pomembna dela prejmejo Abelovo nagrado in Fieldsovo medaljo.

Matematični inštitut Clay je sporočil, da bo vsakomur, ki bo rešil enega od nagradnih problemov tisočletja, podaril milijon dolarjev.

Matematična orodja

Za matematiko ali iskanje odgovorov na matematične probleme se uporabljajo številna orodja.

Starejša orodja

Abakus
Napierjeve kosti, drsno pravilo
Pravilo in kompas
Mentalni izračun

Novejša orodja

Kalkulatorji in računalniki
Programski jeziki
Sistemi računalniške algebre (seznam)
Internetna kratica
programsko opremo za statistično analizo (na primer SPSS).
Programski jezik SAS
Programski jezik R

Oglejte si tudi

Časovna os žensk v matematiki
Ameriško matematično društvo
Društvo za industrijsko in uporabno matematiko
Matematični rodoslovni projekt
Matematična predmetna klasifikacija

Vprašanja in odgovori

V: Kaj je matematika?

O: Matematika je preučevanje števil, oblik in vzorcev. Beseda izhaja iz grške besede μάθημα (máthema), ki pomeni "znanost, znanje ali učenje".

V: Katera so glavna področja matematike?

O: Glavna področja matematike so števila, struktura (algebra), prostor (geometrija) in spremembe (analiza).

V: Kako se matematika uporablja v resničnem svetu?

O: Uporabna matematika je uporabna za reševanje problemov v resničnem svetu. Matematiko uporabljajo ljudje, ki delajo v podjetjih, znanosti, inženirstvu in gradbeništvu.

V: Ali obstaja skrajšana različica besede "matematika"?

O: Da - v državah britanskega Commonwealtha se lahko skrajša na "maths", v Severni Ameriki pa na "math".

V: Kaj pomeni beseda "matematika"?

O: Beseda "matematika" izhaja iz grške besede μάθημα (máthema) in pomeni "znanost, znanje ali učenje".

V: Kakšno vrsto reševanja problemov vključuje uporabna matematika?

O: Uporabna matematika vključuje reševanje problemov v resničnem svetu, s katerimi se srečujejo ljudje, ki delajo v podjetjih, znanosti, inženirstvu in gradbeništvu.