Drsno pravilo (drsnik): definicija, uporaba in zgodovina
Drsno pravilo (drsnik): definicija, uporaba in zgodovina – odkrijte delovanje, vrste, zgodovinski razvoj ter praktične uporabe v znanosti, letalstvu in financah.
Drsnik ali drsna palica je mehanski analogni računalnik, sestavljen iz premičnega drsnika in enega ali več fiksnih delov z natisnjenimi logaritmičnimi lestvicami. Drsno pravilo se uporablja predvsem za množenje in deljenje, pa tudi za "znanstvene" funkcije, kot so koreni, logaritmi in trigonometrija, vendar običajno ne za seštevanje ali odštevanje. Glavna prednost drsnika je hitrost in preprostost izvajanja mnogih računskih operacij brez uporabe elektrike; glavna omejitev pa je, da uporabnik sam ureja mesto decimalne vejice in dobi omejeno natančnost (običajno nekaj pomembnih mest).
Konstrukcija in delovanje
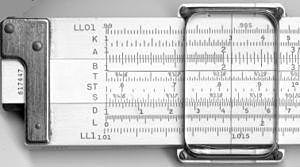
Tipično drsno pravilo sestavljata dve delni: fiksna osnova (podlaga) z eno ali več trakov z oznakami in premični člen (drsnik), ki se poteza vzdolž podlage. Nekatera drsna pravila imajo tudi prozorno drsno okno (cursor), ki omogoča natančno poravnavo lestvic. Lestvice so logaritmično razporejene, kar pomeni, da se seštevanje logaritmov (poravnava) pretvori v množenje števil.
Pogoste lestvice
Drsna pravila imajo standardizirane oznake (imenovane lestvice). Najpogostejše so:
- C in D – osnovni logaritmični trakovi za množenje in deljenje;
- A in B – kvadratne lestvice (uporabne za korene in kvadrate);
- CI – inverzna lestvica C; pomaga pri hitrem deljenju;
- K – kubične lestvice;
- L – linearna lestvica za logaritme (dekadni eksponenti);
- LL – večni niz za eksponentne funkcije in velike/majhne eksponentne vrednosti;
- S, T in ST – trigonometrične lestvice za sinus, tangens in majhne kote.
Specializirana drsna pravila, na primer za letalstvo (npr. E6B) ali finance, vključujejo dodatne posebne lestvice in merila, prilagojena posameznim izračunom.
Kako se uporablja (osnovni primeri)
Multiplikacija (na primer 2 × 3 = 6):
- Poravnajte 1 na lestvici C z 2 na lestvici D (drsnik nad podlago).
- Na lestvici C poiščite 3 in pod njim na lestvici D preberite rezultat 6.
Deljenje (na primer 6 ÷ 3 = 2):
- Poravnajte 3 na C z 6 na D.
- Pod 1 na C na D preberite 2.
Pri vseh izračunih mora uporabnik mentalno določiti pravilno mesto decimalne vejice (t. i. skala mantise). To pomeni, da drsno pravilo daje rezultat v obliki več znamenk brez avtomatske informacije o decimalni premestitvi.
Natančnost in omejitve
Standardna natančnost prenosnih drsnih pravil je približno 2–4 pomembne cifre, odvisno od dolžine in finosti lestvice ter spretnosti uporabnika. Za večjo natančnost so obstajala daljša drsna pravila (npr. 10-, 20- in več centimetrov dolžine) ali cilindrična drsna pravila, ki so podaljševala razdalje lestvic.
Vrste drsnih pravil
- Linearni (ravni) – najpogostejši prenosni oblik;
- Krožni – lestev je zvita v krog, kar omogoča daljšo lestvico na kompaktni napravi;
- Cilindrični – zelo dolga obtekanja lestvice zavita okoli valja za večjo natančnost;
- Specializirana – prilagojena za posebne naloge v letalstvu, medicini, financah ipd.
Zgodovina
William Oughtred in drugi so v 17. stoletju razvili drsno pravilo; drsnik temelji na konceptih Johna Napierja o logaritmih, ki jih je Napier objavil v začetku 17. stoletja (1614). Napierjevo odkritje logaritmov je omogočilo geometrijsko pretvorbo množenja v seštevanje, kar so izkoristili izumitelji, kot je Oughtred, za izdelavo praktičnih instrumentov. V 18. in 19. stoletju so se drsna pravila širila in izpopolnjevala—nastajale so različne oblike, standardne lestvice in specializirane različice. Pred razvojem elektronskih kalkulatorjev je bilo drsno pravilo orodje, ki se je najpogosteje uporabljalo v znanosti in tehniki. V petdesetih in šestdesetih letih 20. stoletja se je uporaba drsnih pravil še naprej povečevala, tudi ko so se postopoma uvajale digitalne računalniške naprave; vendar je okoli leta 1974 zaradi žepnega kalkulatorja drsno pravilo postalo precej zastarelo in večina dobaviteljev je zapustila to dejavnost.
Kje in zakaj so bila drsna pravila pomembna
V času pred množično razširjenostjo elektronskih kalkulatorjev so drsna pravila omogočala hitro in zanesljivo delo in so bila standardna oprema in orodje za inženirje, tehnike, študente in znanstvenike. Zaradi fizične neodvisnosti od električne energije so bila uporabna tudi v poljskih in letalskih razmerah. Danes imajo drsna pravila predvsem zgodovinsko, izobraževalno in zbirateljsko vrednost; nekateri inženirji in ljubitelji jih še vedno uporabljajo zaradi njihovih didaktičnih lastnosti pri razumevanju logaritmov in številskih operacij.
Vzdrževanje in zbirateljstvo
Drsna pravila so običajno izdelana iz lesa, kovine ali plastike; starejši modeli iz lesa z lakirano površino so občutljivi na vlago in ekstremne temperature ter zahtevajo previdno shranjevanje in redko čiščenje. Zbiratelji cenijo redke, dobro ohranjene in specializirane primerke. Obstajajo tudi muzeji in spletne skupnosti, posvečene ohranjanju in razlagi zgodovine drsnih pravil.
Drsnik je bil tako pomembno orodje svoje dobe in ostaja uporaben obisk pri pouku matematike in zgodovine tehnologije, hkrati pa privlačen predmet za zbiralce in navdušence nad analognimi računalniki.

Tipično desetpalčno študentsko drsno pravilo (Pickett N902-T simplex trig)

Drsnik je postavljen tako, da se množi z 2. Vsaka številka na lestvici D (spodaj) je dvakratnik številke nad njo na lestvici C (sredina).
Osnovni pojmi
V svoji najosnovnejši obliki drsno pravilo uporablja dve logaritemski lestvici, ki omogočata hitro množenje in deljenje števil. Ti pogosti postopki so lahko zamudni in nagnjeni k napakam, če jih izvajamo na papirju. Kompleksnejša drsna pravila omogočajo druge izračune, kot so kvadratni koreni, eksponent, logaritem in trigonometrične funkcije.
Matematični izračuni se opravijo tako, da se znak na drsnem sredinskem traku poravna z znakom na enem od fiksnih trakov. Nato lahko opazujemo relativni položaj drugih oznak. Številke, ki so poravnane z oznakami, dajejo približno vrednost produkta, količnika ali drugega izračunanega rezultata.
Uporabnik določi mesto decimalke v rezultatu na podlagi miselne ocene. Pri bolj formalnih izračunih se za sledenje decimalki uporablja znanstveni zapis. Korake seštevanja in odštevanja v izračunu običajno opravimo miselno ali na papirju in ne na drsnem računalu.
Večina drsnikov ima tri linearne trakove enake dolžine. Trakovi so vzporedno poravnani in med seboj povezani, tako da je osrednji trak mogoče vzdolžno premikati glede na druga dva. Zunanja dva trakova sta fiksna, tako da se njun relativni položaj ne spreminja.
Nekatera drsna pravila (modeli "duplex") imajo lestvice na obeh straneh pravila in drsnega traku, druga na eni strani zunanjih trakov in obeh straneh drsnega traku, tretja samo na eni strani (pravila "simplex"). Drsni kazalec z navpično poravnalno črto se uporablja za iskanje ustreznih točk na lestvicah, ki niso druga poleg druge ali so pri dupleksnih modelih na drugi strani pravila. Kazalec lahko zapiše tudi vmesni rezultat na kateri koli lestvici.

Kurzor na drsnem kolesu
Uporaba drsnika za izračun
Množenje
Logaritem pretvori operaciji množenja in deljenja v seštevanje in odštevanje po pravilih log ( x y ) = log ( x ) + log ( y ) {\displaystyle \log(xy)=\log(x)+\log(y)} 











Operacije so lahko "izven lestvice"; na primer zgornji diagram kaže, da drsno pravilo ni postavilo števila 7 na zgornji lestvici nad nobeno število na spodnji lestvici, zato ne daje nobenega odgovora za 2×7. V takšnih primerih lahko uporabnik premakne zgornjo lestvico v levo, dokler se njen desni indeks ne poravna s številom 2, in tako dejansko pomnoži z 0,2 namesto z 2, kot je prikazano na spodnji sliki:
![]()
Pri tem mora uporabnik drsnega merila ne pozabiti ustrezno prilagoditi decimalno vejico, da popravi končni odgovor. Želeli smo najti 2×7, vendar smo namesto tega izračunali 0,2×7=1,4. Zato pravi odgovor ni 1,4, ampak 14. Ponastavitev drsnika ni edini način za reševanje množenj, pri katerih bi dobili rezultate izven lestvice, kot je 2×7; obstajajo še nekatere druge metode:
- (1) Uporabite dvodecetni lestvici A in B.
- (2) Uporabite prepognjene lestvice. V tem primeru postavite levo 1 v C nasproti 2 v D. Premaknite kurzor na 7 v CF in preberite rezultat iz DF.
- (3) Uporabite obrnjeno lestvico CI. Postavite 7 na lestvici CI nad 2 na lestvici D in nato odčitajte rezultat z lestvice D pod 1 na lestvici CI. Ker se 1 pojavlja na dveh mestih na lestvici CI, bo eno od njiju vedno na lestvici.
- (4) Uporabite obrnjeno lestvico CI in lestvico C. Postavite 2 na lestvici CI na 1 na lestvici D in preberite rezultat na lestvici D pod 7 na lestvici C.
Metoda 1 je razumljiva, vendar pomeni izgubo natančnosti. Prednost metode 3 je, da vključuje le dve lestvici.
Oddelek
Spodnja slika prikazuje izračun 5,5/2. Dvojka na zgornji lestvici je postavljena nad 5,5 na spodnji lestvici. Številka 1 na zgornji lestvici leži nad kvocientom 2,75. Obstaja več metod za deljenje, vendar ima tukaj predstavljena metoda to prednost, da končni rezultat ne more biti izven lestvice, saj lahko uporabimo 1 na obeh koncih.

Druge dejavnosti
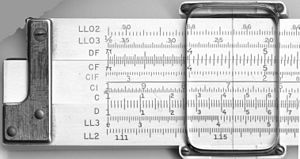
Poleg logaritemskih lestvic imajo nekatera drsna merila druge matematične funkcije kodirane na drugih pomožnih lestvicah. Najbolj priljubljene so bile trigonometrične, običajno sinus in tangens, navadni logaritem (log10) (za jemanje logaritma vrednosti na skali množiteljev), naravni logaritem (ln) in eksponentna lestvica (ex ). Nekatera pravila vključujejo pitagorejsko lestvico za določanje stranic trikotnikov in lestvico za določanje krogov. Druga pravila vsebujejo lestvice za računanje hiperboličnih funkcij. Pri linearnih pravilih so lestvice in njihovo označevanje zelo standardizirani, saj se običajno razlikujejo le glede tega, katere lestvice so vključene in v kakšnem vrstnem redu:
| A, B | logaritemske lestvice z dvema dekadama, ki se uporabljajo za iskanje kvadratnih korenov in kvadratov števil. |
| C, D | enodekadne logaritemske lestvice |
| K | tridesetstopenjska logaritemska lestvica, ki se uporablja za iskanje kubičnih korenov in kubusov števil |
| CF, DF | "zložene" različice lestvic C in D, ki se začnejo od π in ne od enice; te so priročne v dveh primerih. Prvič, kadar uporabnik predvideva, da bo izdelek blizu vrednosti 10, vendar ni prepričan, ali bo nekoliko manjši ali nekoliko večji od 10, se zložene lestvice izognejo možnosti, da bi se oddaljile od lestvice. Drugič, ker je začetek π in ne kvadratni koren iz 10, je množenje ali deljenje s π (kar je običajno v naravoslovnih in tehničnih formulah) poenostavljeno. |
| CI, DI, DIF | "obrnjena" lestvica, ki teče od desne proti levi in se uporablja za poenostavitev korakov 1/x. |
| S | se uporablja za iskanje sinusov in kosinusov na lestvici D |
| T | se uporablja za iskanje tangensov in kotangensov na lestvicah D in DI |
| ST, SRT | se uporablja za sinuse in tangente majhnih kotov ter za pretvorbo stopinj v radian |
| L | linearna lestvica, ki se uporablja skupaj z lestvicama C in D za iskanje logaritmov osnove 10 in potenc 10. |
| LLn | niz logaritemskih lestvic, ki se uporabljajo za iskanje logaritmov in eksponentov števil. |
| Ln | linearna lestvica, ki se uporablja skupaj z lestvicama C in D za iskanje naravnih logaritmov (osnova e) in e x {\displaystyle e^{x}} |
| ||
| Lestvice na sprednji in zadnji strani drsnega merila K&E 4081-3. |
Binarno drsno pravilo, ki ga je leta 1931 izdelal Gilson, je imelo funkcijo seštevanja in odštevanja, omejeno na ulomke.
Korenine in moči
Poznamo enodekadne (C in D), dvodekadne (A in B) in trodekadne (K) lestvice. Za izračun x 2 {\displaystyle x^{2}} 
Za 

Trigonometrija
Lestvice S, T in ST se uporabljajo za trigonometrične funkcije in mnogokratnike trigonometričnih funkcij, za kote v stopinjah. Številna drsna pravila imajo svoje lestvice S, T in ST označene s stopinjami in minutami. Tako imenovani decitrig modeli namesto tega uporabljajo decimalne deleže stopinj.
Logaritmi in eksponentni koeficienti
Logaritme in eksponentne koeficiente osnove 10 najdemo s pomočjo L lestvice, ki je linearna. Nekatera drsna pravila imajo Ln lestvico, ki je za osnovo e.
Ln lestvico je leta 1958 izumil učenec 11. razreda Stephen B. Cohen. Prvotni namen je bil omogočiti uporabniku, da na lestvici Ln izbere eksponent x (v razponu od 0 do 2,3) in prebere ex na lestvici C (ali D) ter e –xna lestvici CI (ali DI). Podjetje Pickett Inc. je dobilo ekskluzivne pravice za lestvico. Kasneje je izumitelj na lestvici Ln ustvaril niz "oznak" za razširitev območja preko meje 2,3, vendar Pickett teh oznak ni nikoli vključil v nobeno od svojih drsnih pravil. []
Seštevanje in odštevanje
Pravil za seštevanje in odštevanje običajno ne uporabljamo, vendar je to mogoče z dvema različnima tehnikama.
Prva metoda za izvajanje seštevanja in odštevanja na lestvicah C in D (ali drugih primerljivih lestvicah) zahteva pretvorbo problema v deljenje. Pri seštevanju je kvocient dveh spremenljivk, povečan za ena krat delitelj, enak njuni vsoti:
x + y = ( x y + 1 ) y {\displaystyle x+y=\left({\frac {x}{y}}+1\right)y}
Pri odštevanju je količnik dveh spremenljivk minus ena krat delitelj enak njuni razliki:
x - y = ( x y - 1 ) y {\displaystyle x-y=\left({\frac {x}{y}}-1\right)y}
Ta metoda je podobna tehniki seštevanja/odštevanja, ki se uporablja za hitra elektronska vezja z logaritemskim številskim sistemom v specializiranih računalniških aplikacijah, kot sta superračunalnik Gravity Pipe (GRAPE) in skriti Markovovi modeli.
Druga metoda uporablja drsno linearno L lestvico, ki je na voljo v nekaterih modelih. Seštevanje in odštevanje se izvaja z drsenjem kazalca v levo (za odštevanje) ali desno (za seštevanje), nato pa se drsnik vrne na 0, da se prebere rezultat.
Fizična zasnova
Standardna linearna pravila
Dolžina drsnega merila je navedena kot nazivna dolžina lestvic. Lestvice na najpogostejših "10-palčnih" modelih so dejansko dolge 25 cm, saj so bile izdelane po metričnih standardih, čeprav nekatera pravila ponujajo nekoliko podaljšane lestvice, da bi poenostavili manipulacijo, kadar se rezultat prelije. Žepna pravila so običajno velika 5 palcev. Modeli, dolgi nekaj metrov, so se prodajali za obešanje v učilnice za namene poučevanja. [1]
Običajno delitve označujejo lestvico z natančnostjo dveh pomembnih številk, tretjo številko pa oceni uporabnik. Nekatera vrhunska drsna merila imajo povečevalna kazala, ki olajšajo pregled nad oznakami. Takšni kazalci lahko učinkovito podvojijo natančnost odčitavanja, kar omogoča, da 10-palčno drsno pravilo služi enako dobro kot 20-palčno.
Razvite so bile tudi druge ugodnosti. Trigonometrične lestvice so včasih dvojno označene, v črni in rdeči barvi, s komplementarnimi koti, tako imenovani "darmstadtski" slog. Dvojna drsna pravila pogosto podvajajo nekatere lestvice na hrbtni strani. Lestvice so pogosto "razdeljene", da se doseže večja natančnost.
Za različne oblike inženiringa, poslovanja in bančništva so bila izumljena specializirana drsna pravila. Pogosto so bili skupni izračuni neposredno izraženi kot posebne lestvice, na primer izračuni posojil, optimalne količine za nakup ali posebne inženirske enačbe. Podjetje Fisher Controls je na primer distribuiralo prilagojeno drsno pravilo, prilagojeno za reševanje enačb, ki se uporabljajo za izbiro ustrezne velikosti industrijskih ventilov za regulacijo pretoka. []
Krožna drsna pravila
Krožna drsna merila so na voljo v dveh osnovnih vrstah: z dvema kazalcema (levo) in z gibljivim diskom in enim kazalcem (desno). Različice z dvema kazalcema opravljajo množenje in deljenje tako, da se med vrtenjem kazalcev okoli krožnice ohranja nespremenjen kot med njima. Različica z enim kazalcem deluje bolj podobno kot standardno drsno merilo z ustrezno poravnavo lestvic.
Osnovna prednost krožnega drsnika je, da se najdaljša dimenzija orodja zmanjša za faktor približno 3 (tj. za π). Na primer, zunanja skala 10 cm krožnega drsnika bi imela največjo natančnost, ki bi bila enaka 30 cm navadnega drsnika. Okrogla drsna pravila prav tako odpravljajo izračune "izven obsega", saj so bile lestvice zasnovane tako, da se "ovijejo"; nikoli jih ni treba preusmeriti, kadar so rezultati blizu 1,0 - pravilo je vedno v obsegu. Vendar se pri necikličnih nespiralnih lestvicah, kot so S, T in LL, dolžina lestvice skrajša, da je dovolj prostora za končne robove.
Krožna drsna merila so mehansko robustnejša in se gibljejo bolj gladko, vendar je njihova natančnost poravnave lestvice občutljiva na centriranje osrednjega čepa; že majhna odmaknitev 0,1 mm od središča čepa lahko povzroči napako poravnave 0,2 mm v najslabšem primeru. Čep pa preprečuje praske na površini in kazalcih. Skale z največjo natančnostjo so nameščene na zunanjih obročih. Pri vrhunskih krožnih pravilih se namesto "deljenih" lestvic uporabljajo spiralne lestvice za bolj zapletene operacije, kot so logaritemske lestvice. Eno osempalčno krožno pravilo najvišjega razreda je imelo 50-palčno spiralno logaritemsko lestvico.
Glavne pomanjkljivosti krožnih drsnikov so težave pri določanju položaja številk na vrtečem se disku in omejeno število lestvic. Druga pomanjkljivost krožnih drsnikov je, da so manj pomembne lestvice bližje središču in imajo manjšo natančnost. Večina učencev se je naučila uporabljati drsna pravila na linearnih drsnih pravilih in ni našla razloga za zamenjavo.
Eno od drsnih meril, ki se še vedno vsakodnevno uporablja po vsem svetu, je E6B. To je krožno drsno pravilo, ki je bilo v tridesetih letih 20. stoletja prvič izdelano za pilote letal, da bi jim pomagalo pri mrtvem računanju. S pomočjo lestvic, natisnjenih na okvirju, pomaga tudi pri različnih opravilih, kot so pretvorba časa, razdalje, hitrosti in temperature, napake kompasa in izračun porabe goriva. Tako imenovano "molitveno kolo" je še vedno na voljo v letalskih trgovinah in se še vedno pogosto uporablja. Medtem ko je GPS zmanjšal uporabo mrtvega tehtanja za navigacijo v zraku in so ročni kalkulatorji prevzeli veliko njegovih funkcij, se E6B še vedno pogosto uporablja kot glavna ali rezervna naprava, večina letalskih šol pa zahteva, da ga njihovi učenci do neke mere obvladajo.
Leta 1952 je švicarska urarska družba Breitling predstavila pilotsko ročno uro z vgrajenim krožnim drsnikom, specializiranim za izračune med letenjem: Breitling Navitimer. Navitimer, ki ga je Breitling imenoval "navigacijski računalnik", je vseboval funkcije za izračun hitrosti, hitrosti/časa vzpenjanja/spuščanja, časa leta, razdalje in porabe goriva ter funkcije za pretvorbo kilometrov v navtične milje in količine goriva v galone in litre.
Materiali
Tradicionalno so bila drsna merila izdelana iz trdega lesa, kot sta mahagonij ali boks, s steklenimi in kovinskimi kazalkami. Vsaj en zelo natančen instrument je bil izdelan iz jekla.
Leta 1895 je japonsko podjetje Hemmi začelo izdelovati drsna pravila iz bambusa, katerega prednost je bila dimenzijska stabilnost, trdnost in naravno samomazanje. Ta bambusova drsna pravila so na Švedskem predstavili septembra 1933 [2], v Nemčiji pa verjetno le malo prej. Lestvice so bile izdelane iz celuloida ali plastike. Kasnejša drsna pravila so bila izdelana iz plastike ali aluminija, pobarvanega s plastiko. Kasnejša kazala so bila iz akrila ali polikarbonata, ki so drsala na teflonskih ležajih.
Vsa premijska drsna pravila so imela vgravirane številke in lestvice, nato pa so bila zapolnjena z barvo ali drugo smolo. Poslikana ali odtisnjena drsna pravila so veljala za slabša, saj so se oznake lahko obrabile. Kljub temu je podjetje Pickett, verjetno najuspešnejše ameriško podjetje za izdelavo drsnih številk, izdelovalo vse tiskane lestvice. Premijska drsna pravila so vsebovala pametne kljuke, da pravilo ne bi po nesreči razpadlo, in odbojnike, ki so ščitili lestvice in kurzor pred drgnjenjem ob namizne plošče. Priporočena metoda čiščenja graviranih oznak je rahlo drgnjenje z jekleno volno. Za poslikana drsna pravila in za tiste, ki so šibkega srca, uporabite razredčeno komercialno tekočino za čiščenje oken in mehko krpo.

Pickettovo krožno drsno merilo z dvema kazalcema. (premer 4,25 in / 10,9 cm) Na hrbtni strani je dodatna skala in en kazalec.

Preprosto krožno drsno merilo, ki ga je izdelalo podjetje Concise Co., Ltd., Tokio, Japonska, z le inverzno, kvadratno in kubično skalo. Na hrbtni strani je priročen seznam 38 metričnih/imperialnih pretvorbenih faktorjev.

Ročna ura Breitling Navitimer s krožnim drsnikom
Zgodovina
Drsno pravilo je bilo izumljeno okoli leta 1620-1630, kmalu po tem, ko je John Napier objavil koncept logaritma. Edmund Gunter iz Oxforda je razvil računsko napravo z eno logaritemsko skalo, ki jo je bilo mogoče z dodatnimi merilnimi orodji uporabljati za množenje in deljenje. Prvi opis te lestvice je leta 1624 v Parizu objavil angleški matematik Edmund Wingate (ok. 1593-1656) v knjigi z naslovom "L'usage de la reigle de proportion en l'arithmetique & geometrie". Knjiga vsebuje dvojno lestvico, ki ima na eni strani logaritemsko, na drugi pa tabelarno lestvico. Leta 1630 je William Oughtred iz Cambridgea izumil krožno drsno pravilo, leta 1632 pa je združil dve Gunterjevi pravili, ki ju je držal skupaj z rokami, in tako izdelal napravo, ki je prepoznavna kot sodobno drsno pravilo. Tako kot njegov sodobnik v Cambridgeu Isaac Newton je tudi Oughtred svoje zamisli zasebno predaval svojim študentom, vendar jih je z zamudo objavil in se tako kot Newton zapletel v zagrizeno polemiko o prednosti s svojim nekdanjim študentom Richardom Delamainom in predhodnimi trditvami Wingata. Oughtredove zamisli so bile objavljene šele v publikacijah njegovega učenca Williama Forsterja leta 1632 in 1653.
Leta 1677 je Henry Coggeshall izdelal dvostopenjsko zložljivo pravilo za merjenje lesa, imenovano Coggeshallovo drsno pravilo. Njegova zasnova in uporaba orodja sta dali drsnemu pravilu namen tudi zunaj matematičnih preiskav.
Leta 1722 je Warner uvedel dvo- in tridesetstopenjsko lestvico, leta 1755 pa je Everard vključil še obrnjeno lestvico; drsno pravilo, ki vsebuje vse te lestvice, se običajno imenuje "večfazno" pravilo.
Leta 1815 je Peter Roget izumil logaritemsko drsno pravilo, ki je vsebovalo lestvico za prikaz logaritma logaritma. To je uporabniku omogočilo neposredno izvajanje izračunov, ki so vključevali korene in eksponente. To je bilo še posebej uporabno za ulomke.
Sodobna oblika
Sodobnejšo obliko je leta 1859 ustvaril francoski artilerijski poročnik Amédée Mannheim, "ki je imel srečo, da je njegovo pravilo izdelalo podjetje nacionalnega ugleda in da ga je francoska artilerija sprejela." V tistem času, ko je inženirstvo postalo priznana poklicna dejavnost, so se drsna pravila začela široko uporabljati v Evropi. V ZDA so se začela uporabljati šele leta 1881, ko je Edwin Thacher predstavil valjasto pravilo. Dvostransko pravilo je leta 1891 izumil William Cox, izdelovalo pa ga je podjetje Keuffel and Esser Co. iz New Yorka.
Astronomsko delo je zahtevalo tudi natančne izračune, zato so v Nemčiji v 19. stoletju v enem od observatorijev uporabljali jekleno drsno pravilo, dolgo približno 2 metra. Na njem je bil pritrjen mikroskop, ki je omogočal natančnost do šestih decimalnih mest.
V drugi svetovni vojni so bombniki in navigatorji, ki so potrebovali hitre izračune, pogosto uporabljali specializirana drsna pravila. Eden od uradov ameriške mornarice je dejansko zasnoval generično "šasijo" za drsna pravila z aluminijastim ohišjem in plastičnim kazalcem, v katerega je bilo mogoče vstaviti celuloidne kartice (potiskane na obeh straneh) za posebne izračune. Postopek je bil izumljen za izračun dosega, porabe goriva in višine za letala, nato pa je bil prilagojen za številne druge namene.
V petdesetih in šestdesetih letih prejšnjega stoletja je bilo drsno pravilo simbol inženirskega poklica (podobno kot je stetoskop simbol zdravniškega poklica).[] Nemški raketni znanstvenik Wernher von Braun je po drugi svetovni vojni, ko se je preselil v ZDA, da bi delal na ameriškem vesoljskem programu, s seboj prinesel dve starinski drsni pravili Nestler iz tridesetih let prejšnjega stoletja. Vse življenje ni uporabljal nobenih drugih žepnih računskih naprav; drsni pravili sta mu odlično služili za hitre ocene konstrukcijskih parametrov raket in drugih številk. Aluminijasta drsna pravila znamke Pickett so bila glede na oglase na škatlah za drsna pravila Pickett's N600 [3] na petih vesoljskih misijah Apollo, tudi na Luni.
Nekateri študenti inženirstva in inženirji so nosili desetpalčna drsna pravila v torbicah za pas, kar je bilo še sredi sedemdesetih let prejšnjega stoletja pogost pojav v študentskih kampusih. Študenti so lahko imeli tudi deset- ali dvajsetpalčno pravilo za natančno delo doma ali v pisarni, s seboj pa so nosili petpalčno žepno drsno pravilo.
Leta 2004 sta raziskovalca na področju izobraževanja David B. Sher in Dean C. Nataro zasnovala novo vrsto drsnega pravila, ki temelji na prosthaferezi, algoritmu za hitro računanje izdelkov, ki je nastal pred logaritmi. Vendar pa je bilo praktično zanimanje za izdelavo takšnega pravila, ki bi preseglo začetni prototip, majhno. [4]
Upadanje
Pomen drsnega merila se je začel zmanjševati, ko so elektronski računalniki, ki so bili v petdesetih letih prejšnjega stoletja nov, a zelo redek vir, v šestdesetih letih prejšnjega stoletja postali široko dostopni tehničnim delavcem. Z uvedbo programa Fortran leta 1957 so računalniki postali praktični za reševanje skromnih matematičnih problemov. IBM je predstavil vrsto cenovno dostopnejših računalnikov, IBM 650 (1954), IBM 1620 (1959), IBM 1130 (1965), namenjenih znanstvenemu in tehničnemu trgu. Programski jezik BASIC Johna Kemenyja (1964) je študentom olajšal uporabo računalnikov. Miniračunalnik DEC PDP-8 je bil predstavljen leta 1965.
Računalniki so spremenili tudi naravo računanja. Pri drsnih pravilih je bil velik poudarek na uporabi algebre, da bi izraze spravili v najbolj izračunljivo obliko. Uporabniki drsnih pravil so preprosto aproksimirali ali izpustili manjše izraze, da bi poenostavili izračun. Program Fortran je omogočil vnos zapletenih formul iz učbenikov, ne da bi se bilo treba truditi s preoblikovanjem. Številčno integriranje je bilo pogosto lažje kot iskanje rešitev v zaprti obliki za zahtevne probleme. Mladi inženir, ki prosi za računalniški čas za rešitev problema, ki bi ga lahko rešil z nekaj potegi na drsnem pravilu, je postal humoren kliše. Številni računalniški centri so imeli na steni obešeno uokvirjeno drsno pravilo s pripisom "V nujnem primeru razbijte steklo".
Naslednji korak k zamenjavi drsnih računal z elektroniko je bil razvoj elektronskih kalkulatorjev za znanstveno in tehnično uporabo. Med prvimi sta bila Wang Laboratories LOCI-2, predstavljen leta 1965, ki je uporabljal logaritme za množenje in deljenje, ter Hewlett-Packard HP-9100, predstavljen leta 1968. HP-9100 je imel poleg eksponentov in logaritmov tudi trigonometrične funkcije (sin, cos, tan). Uporabljal je algoritem CORDIC (coordinate rotation digital computer), ki omogoča izračun trigonometričnih funkcij samo z uporabo operacij premikanja in seštevanja. Ta metoda je olajšala razvoj vedno manjših znanstvenih kalkulatorjev.
Zadnji žebelj v krsto drsnega računala je bila uvedba žepnih znanstvenih kalkulatorjev, med katerimi je bil prvi Hewlett-Packardov HP-35 iz leta 1972. Takšni kalkulatorji so postali znani kot "slide rule" kalkulatorji, saj so lahko opravljali večino ali vse funkcije slide rule. Za večino študentov so bili dragi, saj so stali več sto dolarjev. Medtem ko so bila profesionalna drsna računala lahko tudi precej draga, so v drogerijah pogosto prodajali osnovne plastične modele za manj kot 20 dolarjev. Do leta 1975 pa je bilo mogoče osnovne štirifunkcijske elektronske kalkulatorje kupiti za manj kot 50 USD. Leta 1976 je TI-30 ponujal znanstveni kalkulator za manj kot 25 USD. Po tem času je trg za drsna pravila hitro usahnil, saj so majhni znanstveni kalkulatorji postali cenovno dostopni.

William Oughtred (1575-1660), izumitelj krožnega drsnega merila

Inženir, ki uporablja drsno pravilo. V ozadju je mehanski kalkulator.

TI-30
Prednosti
- Drsno pravilo je nagnjeno k temu, da ublaži zmoto "lažne natančnosti" in pomembnosti. Tipična natančnost, ki je na voljo uporabniku drsnega merila, je približno tri mesta natančnosti. To dobro ustreza večini podatkov, ki so na voljo za vnos v inženirske formule. Pri uporabi sodobnega žepnega kalkulatorja je lahko natančnost prikazana na sedem ali več decimalnih mest, v resnici pa rezultati nikoli ne morejo biti natančnejši od razpoložljivih vhodnih podatkov.
- S pomočjo drsnega pravila je treba nenehno ocenjevati velikostni red rezultatov. Na diapozitivu 1,5 × 30 (kar je enako 45) bo enak rezultat kot 1 500 000 × 0,03 (kar je enako 45 000). Inženir mora nenehno ugotavljati razumnost rezultatov, kar lahko izgubi, če številke neprevidno vnese v računalniški program ali kalkulator.
- Pri zaporedju množenj ali deljenj z istim številom lahko odgovor pogosto določimo že s pogledom na drsnik brez kakršne koli manipulacije. To je lahko še posebej uporabno pri izračunavanju odstotkov, npr. pri rezultatih testov, ali pri primerjanju cen, npr. v dolarjih na kilogram. Več izračunov hitrosti, časa in razdalje lahko z drsnim merilom opravite brez uporabe rok in z enim samim pogledom.
- Drsno pravilo ni odvisno od elektrike.
- Drsno pravilo je tehnologija, ki jo je mogoče zlahka ponoviti. Na podlagi danega primera drsnega pravila lahko sposoben obrtnik iz osnovnih materialov z uporabo neindustrijskih postopkov izdela še več.
- Drsna pravila so zelo standardizirana, zato se ob prehodu na drugo pravilo ni treba ničesar ponovno učiti.
- Drsna pravila so vsestranska in jih je mogoče uporabljati v razmerah in okoljih, v katerih ima uporabnik manjšo spretnost (na primer zaradi uporabe zaščitnih rokavic). Nasprotno pa je v takšnih primerih težko upravljati kalkulator - pri drsnem pravilu je malo verjetno, da bi prišlo do napake, podobne tisti, ki je posledica pomotnega pritiska na napačen gumb na kalkulatorju.
- Drsna pravila so lahko izdelana iz kartona ali papirja. Veliko brezplačnih tabel ali specializiranih računskih naprav iz kartona so pravzaprav specializirana linearna ali krožna drsna pravila.
Ena od prednosti uporabe drsnega merila in elektronskega kalkulatorja je, da lahko pomemben izračun preverimo z obema; ker sta instrumenta tako različna, je malo možnosti, da bi dvakrat naredili isto napako.
Slabosti
- Napake lahko nastanejo zaradi mehanske nenatančnosti.
- Izračuni z drsnikom so zaradi analognih vhodov in izhodov omejeno natančni. Nasprotno pa imajo zaradi diskretnih številskih vhodov in elektronskih operacij s plavajočo vejico tudi skromni sodobni kalkulatorji izhodno ločljivost vsaj šest pomembnih številk.
Sorodne strani
Vprašanja in odgovori
V: Kaj je drsno pravilo?
O: Drsnik je mehanski analogni računalnik, ki se uporablja predvsem za množenje in deljenje ter znanstvene funkcije, kot so koreni, logaritmi in trigonometrija.
V: Katere so različne vrste drsnih pravil?
O: Drsna pravila so lahko linearna ali krožna in imajo standardiziran nabor oznak ali lestvic, ki se uporabljajo za matematične izračune. Nekatera drsna pravila za posebno uporabo so bila izdelana za letalstvo ali finance s posebnimi lestvicami za te namene.
V: Kdo je izumil drsno pravilo?
O: Drsno pravilo je izumil William Oughtred na podlagi dela Johna Napierja o logaritmih.
V: Kdaj so bili razviti elektronski kalkulatorji?
O: Elektronski kalkulatorji so bili razviti pred letom 1970, vendar je okoli leta 1974 žepni kalkulator povzročil, da je drsno pravilo postalo precej zastarelo.
V: Kaj so ljudje najpogosteje uporabljali v znanosti in tehniki, preden so bili razviti elektronski kalkulatorji?
O: Pred razvojem elektronskih kalkulatorjev so ljudje v znanosti in tehniki najpogosteje uporabljali drsno računalo.
V: Kako dolgo so ljudje še uporabljali drsno pravilo, ko so se pojavile digitalne računalniške naprave?
O: Ljudje so drsno računalo uporabljali še v petdesetih in šestdesetih letih prejšnjega stoletja, čeprav so se postopoma uvajale digitalne računalniške naprave.
Iskati