Deljenje
V matematiki beseda "deljenje" pomeni operacijo, ki je nasprotna množenju. Nekateri simboli za deljenje so lahko poševnica, črta ali znak za deljenje ( ÷ {\displaystyle \div }
), kot npr:
6 / 3 {\displaystyle 6/3\,} ali
6 3 {\displaystyle {\frac {6}{3}}} ali 
6 ÷ 3. {\displaystyle 6\div 3.} 
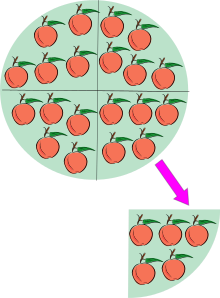
Vsaka od teh treh vrst pomeni "6 deljeno s 3", odgovor pa je 2. Prvo število je dividenda (6), drugo pa delitelj (3). Rezultat (ali odgovor) je količnik. Pri celih številih se vsak preostanek imenuje "ostanek" (na primer 14/4 da 3, pri čemer je ostanek 2, kot število 3+2⁄4, enako kot 3+1⁄2 ali 3,5).
Številke so lahko zelo velike, na primer dvesto: 200/5 = 40 ali 7 milijard: 7.000.000.000.000 / 1000 = 7.000.000 (enako 7 milijonov).
20 : 4 = 5 {\displaystyle 20:4=5} 
Z množenjem
Če je c krat b enako a, je zapisano kot:
c × b = a {\displaystyle c\krat b=a} 
če b ni nič, potem je a, deljeno z b, enako c, kar je zapisano kot:
a b = c {\displaystyle {\frac {a}{b}}=c} 
Na primer,
6 3 = 2 {\displaystyle {\frac {6}{3}}=2} 
od .
2 × 3 = 6 {\displaystyle 2\krat 3=6}
.
V zgornjem izrazu se a imenuje dividenda, b delitelj, c pa kvocient.
x 0 = ? {\displaystyle {\frac {x}{0}}=? } 
...ni opredeljen.
Zapis
Deljenje najpogosteje prikažemo tako, da dividendo postavimo nad delitelja, med njima pa je vodoravna črta, imenovana tudi vinkula. Na primer, a deljeno z b je zapisano
a b . {\displaystyle {\frac {a}{b}}. } 
To lahko glasno preberete kot "a deljeno z b" ali "a nad b". Delitev lahko izrazimo v eni vrstici tako, da zapišemo dividendo, nato poševnico in nato delitelja, kot sledi:
a / b . {\displaystyle a/b.\,} 
To je običajen način določanja delitve v večini računalniških programskih jezikov, saj jo je mogoče preprosto vnesti kot preprosto zaporedje znakov.
Tipografska različica, ki je na pol poti med tema dvema oblikama, uporablja poševnico, vendar dviga dividendo in znižuje delitelj:
a⁄b .
Za prikaz ulomka lahko uporabite katero koli od teh oblik. Ulomek je izraz za deljenje, kjer sta tako dividenda kot delitelj celi števili (čeprav ju običajno imenujemo števec in imenovalec). Ulomek je sprejet način zapisovanja števil. Ni vedno pričakovano, da je rezultat deljenja zapisan z decimalnimi števili.
Manj pogost način prikazovanja delitve je uporaba obeležja (ali znaka za delitev) na ta način:
a ÷ b . {\displaystyle a\div b. } 
V osnovni aritmetiki pa se ta oblika uporablja precej pogosto. Obelus se uporablja tudi za predstavitev same operacije deljenja, na primer kot oznaka na tipki kalkulatorja.
V nekaterih neangleško govorečih kulturah je "a deljeno z b" zapisano a : b. Vendar je v angleščini dvopičje omejeno na izražanje sorodnega pojma razmerja (a : b pomeni "a je do b").
Sorodne strani
- Delitelj, drug pomen kot število, ki enakomerno deli znesek.
- Delitev z dvema
- Preostanek
Vprašanja in odgovori
V: Kaj pomeni beseda "delitev" v matematiki?
O: V matematiki je deljenje operacija, ki je nasprotna množenju.
V: Kateri so simboli za deljenje?
O: Simbola za deljenje sta poševnica ( / ) in črta za ulomek.
V: Kaj je dividenda v problemu deljenja?
O: Prvo število v problemu deljenja se imenuje dividenda.
V: Kaj je delitelj v delitveni nalogi?
O: Drugo število v delitveni nalogi se imenuje delitelj.
V: Kako se imenuje rezultat delitvenega problema?
O: Rezultat delitvenega problema se imenuje količnik, preostali del v obliki celih števil pa se imenuje "ostanek".
V: Ali lahko pri deljenju uporabimo velika števila?
O: Da, pri deljenju lahko uporabimo zelo velika števila, na primer dvesto ali sedem milijard.
