Množenje: definicija, lastnosti, primeri in zakonitosti
Množenje: definicija, lastnosti, zakonitosti in jasni primeri, od ponavljajočega seštevanja do skaliranja, komutativnost in izjeme za matrike ter vektorje
Množenje je aritmetična operacija za ugotavljanje produkta dveh števil. Pogosto ga razumemo kot ponavljajoče se seštevanje ali kot škalarni pomnožek, pri katerem eno količino povečamo (skaliramo) z drugo. Množenje je ena od osnovnih računskih operacij, poleg seštevanja, odštevanja in deljenja.
Zapis in nazivlje
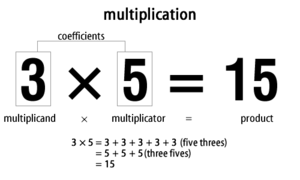
Množenje običajno zapišemo z znakom × ali ·, primer: 3 × 5 = 15. Števili, ki ju množimo, imenujemo faktorja ali koeficienta — nekateri avtorji razlikujejo multiplikand (število, ki ga množimo) in multiplikator (število, s katerim množimo). Rezultat množena imenujemo produkt. Z zapisom pogosto srečamo tudi večprodukt, npr. 2 × 3 × 4 = 24.
Geometrijska in praktična razlaga
Z naravnimi števili lahko množenje razlagamo kot število ploščic v pravokotniku, kjer je eno od števil enako številu ploščic na eni strani, drugo pa številu ploščic na drugi strani. Z realnimi števili predstavlja produkt površino pravokotnika, kjer je eno število dolžina ene stranice, drugo pa dolžina druge.
Lastnosti množenja
- Komutativnost: vrstni red faktorjev pri množenju celih, racionalnih, realnih in kompleksnih števil ne vpliva na produkt: npr. 4 × 6 = 6 × 4. To potrjuje tudi praksa za cela števila, racionalna števila, realna in kompleksna števila. Pri nekaterih strukturah (npr. kvaternioni, vektorji v smislu vektorskega produkta ali matrike) komutativnost ne velja.
- Asociativnost: (a × b) × c = a × (b × c). Zato lahko pri množenju več števil zapišemo produkt brez oklepajev, če vrstni red združevanja ne zanima.
- Distributivnost glede na seštevanje: a × (b + c) = a × b + a × c. To lastnost pogosto uporabljamo pri razširjanju izrazov in pri računskih strategijah.
- Enota množenja: 1 je multiplikativni identiteta, saj a × 1 = a za vsako število a.
- Lastnost nič: a × 0 = 0. Če je eden faktorjev 0, je produkt vedno 0.
- Obratna operacija: Deljenje je inverzna operacija množenju, razen kadar množitelj je 0 (deljenje z 0 ni definirano).
Množenje v različnih strukturah števil
Množenje ima različne pomene glede na množico, s katero delamo:
- Naravna števila: predstavlja ponavljajoče se seštevanje (n × m = seštevek n-krat m). Primer: 3 × 5 je seštevek treh petk ali petih trojk, rezultat 15.
- Cela in racionalna števila: pravila za znak veljajo: + × + = +, + × − = −, − × − = +. Pri ulomkih množimo števci in imenovalci: (a/b) × (c/d) = (ac)/(bd).
- Realna in kompleksna števila: množenje razširimo na decimale in komplekse (uvedemo računska pravila za imaginarno enoto i tako, da i² = −1).
- Matrično in vektorsko množenje: pri matričnem množenju vrstni red pomemben — A·B ni nujno enako B·A; vektorski produkt v 3D prostoru je antikomutativen (u × v = − v × u) in daje vektor, ne skalar.
- Kvaternioni: nekomutativna razširitev kompleksnih števil z lastnimi pravilniki množenja.
Množenje z negativnimi števili, ulomki in decimalami
Pri množenju negativnih števil veljajo znana pravila znakov (glej zgoraj). Pri ulomkih množimo neposredno števce in imenovalce; če želimo pomnožiti mešana števila, jih najprej pretvorimo v nepravi ulomek. Pri decimalnih številih štejemo skupno število decimalnih mest v faktorjih in jih upoštevamo v produktu (npr. 1,2 × 3,45 = 4,14).
Množenje kot ponavljajoče se seštevanje in kot skaliranje
Opredelitev množenja kot ponavljajočega se seštevanja je uporabna pri kardinalnih številih in pri naravnih številih. Natančnejša in širša predstava je, da množenje deluje kot skaliranje: pomnožimo dolžino ali količino z merilom. Na animaciji (opisano v izvirniku) se to jasno pokaže — modra točka, postavljena na enico, se pri množenju z X premakne na X; ta interpretacija velja tudi za X manjši od 1 ali za negativna X (v tem primeru je skaliranje zrcaljenje in spreminjanje magnitude).
Primeri in računske tehnike
- Osnovni primer: 3 × 5 = 15 (tudi: seštevek petih trojk ali treh petk).
- Računske tehnike: razširjanje z distributivnim zakonom (npr. 23 × 45 = 23 × (40 + 5) = 920 + 115 = 1035), dolg način množenja, množenje poševno v mislih s pomočjo tabel množenja.
- Množenje ulomkov: (2/3) × (9/4) = (18/12) = 3/2 (po krajšanju).
- Množenje decimal z negativnimi: −2,5 × 4 = −10.
Pomembne opombe
- Pri množenju več članov trimamo oklepaje z upoštevanjem asociativnosti in distributivnosti.
- Zaporedje operacij (PEMDAS/BODMAS) pravi, da se množenje izvaja pred seštevanjem in odštevanjem, razen če oklepaji določajo drugače.
- Čeprav večina številskih sistemov ohranja komutativnost množenja, nekatere algebraične strukture (matrike, kvaternioni, neke operacije na vektorjih) komutativnosti nimajo.
Nasprotje množenja je deljenje, ki proizvodi faktor, kadar poznamo produkt in enega od faktorjev (če množitelj ni 0).
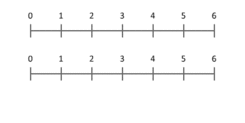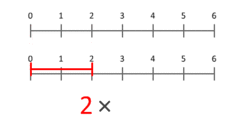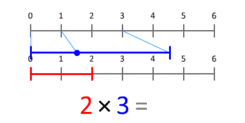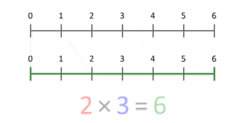
Tabela za množenje
Učitelji pri poučevanju množenja od učencev običajno zahtevajo, da si zapomnijo tabelo prvih 9 števil.
| Tabela 6 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Tabela za množenje | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Sorodne strani
- Dodatek
- Kvadratna številka
- Odštevanje
Vprašanja in odgovori
V: Kaj je množenje?
O: Množenje je aritmetična operacija za ugotavljanje produkta dveh števil v matematiki. Pogosto se predstavlja s simboli, kot sta × in ⋅.
V: Kako se imenujeta dve števili, ki ju je treba pomnožiti?
O: Dve števili, ki ju je treba pomnožiti, se imenujeta "koeficienti" ali ločeno "multiplikand" in "multiplikator".
V: Ali je množenje komutativno?
O: Da, o množenju med številoma pravimo, da je komutativno - kadar vrstni red števil ne vpliva na vrednost produkta. To velja za cela, racionalna, realna in kompleksna števila. Vendar to ne velja za kvaternione, vektorje ali matrike.
V: Kako lahko razlagamo množenje kardinalnih števil?
O: Množenje kardinalnih števil lahko razlagamo kot skaliranje količin - ko eno število (mnogokratnik) skalirate tako, da se pika, postavljena na mesto 1, znajde v določeni točki (mnogokratnik).
V: Kako lahko predstavimo tri, pomnoženo s pet?
O: Tri, pomnoženo s pet, lahko zapišemo kot 3 × 5 = 15 ali kot "tri krat pet je enako petnajst".
V: Kaj je nasprotje množenja?
O: Nasprotje množenja je deljenje.
Iskati