Pi

Pi (ali π) je matematična konstanta. Je razmerje med razdaljo okoli kroga in premerom kroga. Tako dobimo število, ki je vedno enako. Vendar je to število precej nenavadno. Število se začne kot 3,141592653589793 ... in se nadaljuje brez konca. Takšna števila imenujemo iracionalna števila.

Premer je največja kordina, ki jo lahko umestimo v krog. Gre skozi središče kroga. Razdalja okoli kroga se imenuje obseg. Čeprav sta premer in obseg za različne kroge različna, ostaja število pi konstantno: njegova vrednost se nikoli ne spremeni. To je zato, ker je razmerje med obsegom in premerom vedno enako.

π = C d {\displaystyle \pi ={\frac {C}{d}}} $\pi ={\frac {C}{d}}$ (pi je enak deležu obsega in premera).

Pi je neskončen niz številk

Približevanje

Pi se pogosto uradno zapiše kot $π$ ali grška črka π kot bližnjica. Pi je tudi iracionalno število, kar pomeni, da ga ni mogoče zapisati kot ulomek ( a b {\displaystyle a \over b} $a \over b$ ), kjer sta "a" in "b" celi števili. To v bistvu pomeni, da se številke števila pi, ki so desno od decimalke, v neskončnost ne ponavljajo v vzorcu in da natančne vrednosti števila pi ni mogoče zapisati kot število. Pi lahko le približamo ali izmerimo do vrednosti, ki je dovolj blizu za praktične namene.

Vrednost blizu števila pi je 3,141592653589793238462643... Običajni približek števila pi je 22 7 {\displaystyle 22 \over 7} $22 \over 7$ , ki daje približno 3,14285714. Ta približek je za 0,04 % oddaljen od prave vrednosti števila pi. Čeprav je ta približek večinoma sprejet za uporabo v resničnem življenju, je ulomek 355 113 {\displaystyle 355 \over 113} $355 \over 113$ natančnejši (da približno 3,14159292) in ga lahko uporabimo, kadar potrebujemo vrednost, ki je bližje pi. Z računalniki lahko dobimo boljše približke števila pi.

Marca 2019 je Emma Haruka Iwao izračunala vrednost števila pi na 31,4 bilijona številk.

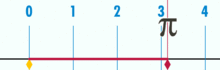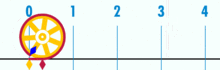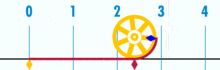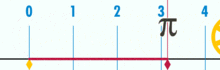
Diagram, ki prikazuje, kako lahko π najdemo s pomočjo kroga s premerom ena. Obod tega kroga je π.

Zgodovina

Vrednost števila pi so poznali že staroindijski matematiki, kot sta Bhaskaracharya in Aryabhatta.

Matematiki poznajo pi že tisočletja, saj se prav toliko časa ukvarjajo s krogi. Že tako stare civilizacije, kot so bili Babilonci, so znale približati pi na več številk, na primer na delček 25/8 in 256/81. Večina zgodovinarjev meni, da stari Egipčani niso imeli pojma π in da je ujemanje naključje.

Prva pisna omemba števila pi sega v leto 1900 pred našim štetjem. Okoli leta 1650 pred našim štetjem je Egipčan Ahmes navedel vrednost v papirusu Rhind. Babilonci so ugotovili, da je vrednost števila pi nekoliko večja od 3, in sicer tako, da so naredili velik krog, nato pa na obod in premer nalepili kos vrvi, zabeležili njuni razdalji in nato delili obod s premerom.

Poznavanje števila pi se je vrnilo v Evropo in prišlo v roke Hebrejcev, ki so to število zapisali v del Svetega pisma, imenovanega Stara zaveza. Po tem je bil najpogostejši način iskanja števila pi ta, da so znotraj kroga narisali obliko z veliko stranicami in s pomočjo površine oblike našli število pi. Grški filozof Arhimed je na primer za iskanje vrednosti števila pi uporabil obliko mnogokotnika s 96 stranicami, Kitajci pa so leta 500 n. št. za iskanje vrednosti števila pi uporabili mnogokotnik s 16 384 stranicami. Grki, kot je bil Anaksagora iz Klazomene, so se ukvarjali tudi z ugotavljanjem drugih lastnosti kroga, na primer, kako iz krogov narediti kvadrate in kvadrat števila pi. Od takrat so številni ljudje skušali ugotoviti vse natančnejše vrednosti števila pi.

Zgodovina pi
Filozof	Datum	Približevanje
Klavdij Ptolemaj	okoli leta 150 n. št.	3.1416
Zu Chongzhi	430-501 CE	3.1415929203
al-Khwarizmi	okoli leta 800 n. št.	3.1416
al-Kashi	okoli leta 1430	3.14159265358979
Viète	1540-1603	3.141592654
Roomen	1561-1615	3.14159265358979323
Van Ceulen	okoli leta 1600	3.14159265358979323846264338327950288

V 16. stoletju so bili na voljo vedno boljši načini za določitev števila pi, kot je zapletena formula, ki jo je razvil francoski pravnik François Viète. Grški simbol "π" je bil prvič uporabljen v eseju, ki ga je leta 1706 napisal William Jones.

Matematik Lambert je leta 1761 dokazal, da je število pi iracionalno; to pomeni, da ga po običajnih standardih ni mogoče zapisati kot ulomek. Drug matematik po imenu Lindeman je leta 1882 pokazal, da je pi del skupine števil, znanih kot transcendentala, to so števila, ki ne morejo biti rešitev polinomske enačbe.

Pi lahko poleg krogov uporabimo tudi za ugotavljanje številnih drugih stvari. Lastnosti števila pi so omogočile, da se poleg geometrije, ki preučuje oblike, uporablja tudi na številnih drugih področjih matematike. Nekatera od teh področij so kompleksna analiza, trigonometrija in serije.

Pi v resničnem življenju

Danes obstajajo različni načini za izračun številnih števk števila π. Vendar je njihova uporaba omejena.

Pi lahko včasih uporabimo za določitev površine ali obsega kroga. Če želite ugotoviti obseg kroga, uporabite formulo C (obseg) = π krat premer. Če želite ugotoviti površino kroga, uporabite formulo π (polmer²). To formulo včasih zapišemo kot A = π r 2 {\displaystyle A=\pi r^{2}} $A=\pi r^{2}$ , kjer je r spremenljivka za polmer kroga, A pa spremenljivka za površino kroga.

Izračunati obseg kroga z napako 1 mm:

Za polmer 30 metrov so potrebne 4 številke.
10 številk za polmer, ki je enak polmeru Zemlje
15 številk za polmer, ki je enak razdalji od Zemlje do Sonca.

Ljudje običajno praznujejo 14. marec kot dan števila pi, saj se 14. marec piše tudi kot 3/14, kar predstavlja prva tri števila 3,14 v približku števila pi. Dan števila pi se je začel leta 2001.

Sorodne strani

Krog

Vprašanja in odgovori

V: Kaj je število ً?

O: ً je matematična konstanta, ki je razmerje med obsegom kroga in njegovim premerom.

V: Kaj se s tem dobi?

O: To je število, ki je vedno enako.

V: Kako se to število začne?

O: Število se začne kot 3,141592653589793 ... in se nadaljuje brez konca.

V: Kakšne vrste so ta števila?

O: Ta števila imenujemo iracionalna števila.

V: Kakšen je premer kroga?

O: Premer kroga je največja kordina, ki jo lahko vtaknemo vanj skozi njegovo središče.
V: Kaj je obseg kroga? O: Razdalja okoli kroga se imenuje njegov obseg.

V: Ali je pi konstanten ne glede na različne kroge? O: Da, pi ostaja konstanten ne glede na različne kroge, saj razmerje med njihovim obsegom in premerom vedno ostaja enako.