Krog: definicija, lastnosti, polmer, premer, obseg in površina
Krog: jasna definicija, lastnosti in ključne formule za polmer, premer, obseg in površino. Enostavne razlage, primeri in hitri izračuni za lažje učenje.
Krog je okrogla dvodimenzionalna oblika, sestavljena iz vseh točk v ravnini, ki ležijo znotraj in na robu določene oddaljenosti od enega samega središča. Pogosto se v strogi matematični terminologiji loči med krožnico (le rob, torej množica točk, ki so natanko enako oddaljene od središča) in krogom (zapolnjena notranjost skupaj z robom). V slovenščini se izraza v praksi včasih uporabljata zamenljivo.
Polmer in središče
Polmer kroga je črta, ki povezuje središče kroga s katero koli točko na njegovem robu. Matematiki za dolžino polmera običajno uporabljajo črko r. Središče kroga je točka, ki je enako oddaljena od vseh točk na krožnici; z njega merimo polmer v vseh smereh.
Premer
Premer kroga je ravna črta, ki poteka od ene do druge strani kroga in skozi središče. Matematiki za dolžino premera pogosto uporabljajo črko d. Premer je dvakratnik polmera, torej velja d = 2r.
d = 2 r {\displaystyle d=2\ r}
Obseg (krožnica)
Obod kroga (pogosteje imenovan tudi krožnica kot dolžina roba) je dolžina črte, ki obdaja krog. Za dolžino oboda se pogosto uporablja črka C (iz angleške besede circumference) ali v slovenskih besedilih tudi O. Obseg lahko izrazimo z uporabo polmera ali premera:
- C = 2·π·r
- C = π·d
To pomeni, da je obseg enak dvakratniku polmera pomnoženemu s številom π.
Število π
Število π (zapisano kot grška črka pi) je razmerje med dolžino obsega in dolžino premera kroga. Kot ulomek je π približno enako 22⁄7 ali 335/113 (ta je natančnejša), kot decimalno število pa približno 3,1415926535. V sodobni matematiki je znano, da je π iracionalno (ne moremo ga izraziti kot natančnega ulomka celih števil) in tudi transcendentno (ni ničla nobenega ne-nicelnega polinomskega izraza s celoštevilski koeficienti).
Površina kroga
Površina znotraj kroga, pogosto označena z A ali v nekaterih besedilih z a, je odvisna od polmera in se izračuna po formuli:
- A = π·r²
Če želimo površino izraziti preko premera, uporabimo A = π·(d/2)² = (π·d²)/4.
Dodatne lastnosti in izrazi
- Dolžina loka krožnice z centralnim kotom θ (izraženim v radianih) je L = r·θ.
- Površina krožnega sektorja s kotom θ (v radianih) je A_sektor = ½·r²·θ.
- Chord (struna) je daljica, ki povezuje dve točki na krožnici; največja struna je premer.
- Tangenta je premica, ki se krožnice dotika v eni točki in je pravokotna na radij, potegnjen do točke dotika.
- Koncentrični krogi imajo isto središče, različne polmere.
Primeri izračuna
Primer 1: Krog s polmerom r = 3 cm.
- Obseg: C = 2·π·3 ≈ 18,85 cm (za π ≈ 3,14159).
- Površina: A = π·3² = 9·π ≈ 28,27 cm².
Primer 2: Krog s premerom d = 10 m.
- Polmer: r = 5 m.
- Obseg: C = π·10 ≈ 31,42 m.
- Površina: A = π·5² = 25·π ≈ 78,54 m².
Uporaba
Krogi in krožnice se pojavljajo v mnogih področjih: v geometriji in trigonometriji, v inženirstvu (krožne gredi, kolesa), v arhitekturi, pri merjenju površin in obsegov, pa tudi v naravi in fiziki (cikel gibanja, valovanja). Razumevanje osnovnih odnosov med polmerom, premerom, obsegom in površino omogoča reševanje praktičnih problemov in nadaljnje matematične izpeljave.

Krog
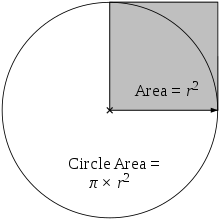
Površina kroga je enaka π-kratniku površine sivega kvadrata.
Izračun π
π lahko izmerimo tako, da narišemo velik krog, izmerimo njegov premer (d) in obseg (C). To je zato, ker je obseg kroga vedno π krat večji od njegovega premera.
π = C d {\displaystyle \pi ={\frac {C}{d}}}
π lahko izračunamo tudi samo z matematičnimi metodami. Večina metod, ki se uporabljajo za izračun vrednosti π, ima zaželene matematične lastnosti. Vendar jih je težko razumeti brez poznavanja trigonometrije in računa. Nekatere metode pa so dokaj preproste, kot je na primer ta oblika Gregorjeve-Leibnizove vrste:
π = 4 1 - 4 3 + 4 5 - 4 7 + 4 9 - 4 11 ⋯ {\displaystyle \pi ={\frac {4}{1}}-{\frac {4}{3}}+{\frac {4}{5}}}-{\frac {4}{7}}+{\frac {4}{9}}-{\frac {4}{11}}\cdots }
Čeprav je to vrsto enostavno zapisati in izračunati, ni lahko razumeti, zakaj je enaka π. Lažje razumljiv pristop je narisati namišljen krog s polmerom r s središčem v izhodišču. Potem bo vsaka točka (x,y), katere oddaljenost d od izvora je manjša od r, izračunanega s Pitagorovim izrekom, znotraj kroga:
d = x 2 + y 2 {\displaystyle d={\sqrt {x^{2}+y^{2}}}}
Z iskanjem množice točk znotraj kroga lahko ocenimo površino kroga A. Na primer z uporabo celoštevilskih koordinat za velik r. Ker je površina A kroga π krat kvadrat polmera, lahko π aproksimiramo z uporabo:
π = A r 2 {\displaystyle \pi ={\frac {A}{r^{2}}}}
Sorodne strani
- Sfera
Vprašanja in odgovori
V: Kaj je krog?
O: Krog je okrogla, dvodimenzionalna oblika. Vse točke na robu kroga so enako oddaljene od središča.
V: Kaj matematiki uporabljajo za predstavitev dolžine polmera kroga?
O: Matematiki za dolžino polmera kroga uporabljajo črko r.
V: Kaj je v krožnicah zapisano kot O?
O: Središče kroga je pogosto zapisano kot O.
V: Kako dolg je premer kroga?
O: Premer kroga (kar pomeni "po vsej dolžini") je ravna črta, ki poteka od ene strani do nasprotne in prav skozi središče kroga. Je enak dvakratniku njegovega polmera (d je enak dvakratniku r).
V: Katero črko matematiki uporabljajo za predstavitev obsega?
O: Matematiki uporabljajo črko C za obseg, kar pomeni "vse naokoli".
V: Kako lahko izračunamo površino znotraj kroga?
O: Površino A znotraj kroga lahko izračunamo tako, da njegov polmer pomnožimo s samim seboj in nato pomnožimo z ً (A je enako ً krat r krat r).
Iskati




