AlegsaOnline.com

Pitagorov izrek (a²+b²=c²): definicija, dokazi in primeri uporabe

Pitagorov izrek (a²+b²=c²): jasna definicija, različni dokazi, praktični primeri in uporabe v matematiki ter vsakdanjem življenju.

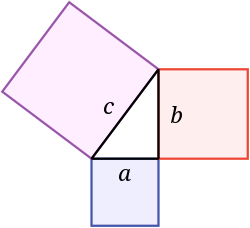
Avtor: Leandro Alegsa Datum ustvarjanja: 20. junij 2021 Zadnja posodobitev: 30. avgust 2025

simple.wikipedia.org · Public domain

Pitagorov izrek (a² + b² = c²) je v matematiki izjava o stranicah pravokotnega trikotnika. Če sta dolžini krakov a in b, dolžina hipotenuze pa c, velja:

a 2 + b 2 = c 2 {\displaystyle a^{2}+b^{2}=c^{2}} $a^{2}+b^{2}=c^{2}$

Ena stranica, ki leži nasproti pravega kota (90 stopinj), je hipotenuza in je vedno najdaljša stranica trikotnika. Stranici ob pravem kotu imenujemo kraka.

Ime izreka izvira po grškem matematiku Pitagori, čeprav so temelje in posebne primere izreka poznali že stare civilizacije (npr. Babilonci, Indijci, Kitajci). Obstaja več sto različnih dokazov tega izreka.

Kaj izrek pomeni

Poleg geometrijske izjave o površinah kvadratov na stranicah pravi izrek tudi, da je v pravokotnem trikotniku kvadrat dolžine hipotenuze enak vsoti kvadratov dolžin obeh krakov. To je osnova za izračun dolžin v številnih praktičnih problemih.

Vrste dokazov

Dokaze izreka običajno razdelimo v več skupin; najpogostejše so:

geometrijski dokazi (npr. dokaz z urejanjem ali s pomočjo podobnih trikotnikov),
algebraični oziroma koordinatni dokazi (postavitev trikotnika v koordinatni sistem),
dokazi z uporabo podobnosti trikotnikov (klasičen evklidski pristop),
analitični in vektorski dokazi (uporaba skalarnega produkta ali Pitagorovega izreka kot posebnega primera zakona kosinov).

Kratek opis nekaj dokazov

Dokaz z urejanjem (rearanžiranjem): v kvadrat, katerega stranica je a + b, lahko vstavimo štiri enaka pravokotna trikotnika tako, da v sredini ostane kvadrat s stranico c. Primerjava površin velikega kvadrata ( (a+b)² ) in vsote štirih trikotnikov ter notranjega kvadrata privede do enačbe 4·(ab/2) + c² = (a+b)², kar po poenostavitvi daje a² + b² = c².

Dokaz s podobnimi trikotniki: padec višine iz pravega kota na hipotenuzo razdeli prvotni trikotnik na dva trikotnika, ki sta podobna med seboj in tudi s prvotnim trikotnikom. Iz razmerij stranic teh podobnih trikotnikov sledijo relacije a² = c·d in b² = c·e (kjer d in e predstavljata odseka hipotenuze), katerih vsota daje a² + b² = c².

Koordinatni dokaz: vstavimo pravokotni trikotnik v koordinatni sistem z enim krakom vzdolž osi x (dolžina a) in drugim vzdolž osi y (dolžina b). Koordinati točke nasproti pravega kota sta (a,0) in (0,b), razdalja med tema točkama je sqrt((a-0)² + (0-b)²) = sqrt(a² + b²), kar je dolžina hipotenuze c, od tod c² = a² + b².

Posledice in lastnosti

Zakon kosinov je splošna oblika Pitagorovega izreka za poljuben trikotnik: c² = a² + b² − 2ab·cos(γ). Če je γ = 90°, se zadnji člen izniči in dobimo Pitagorov izrek.
Obrat izreka: če v trikotniku za stranice velja a² + b² = c², potem je kot nasproti stranice c pravi kot. To je uporabna karakterizacija za preverjanje, ali je trikotnik pravokoten.
Pitagorejske trojice: to so naravna števila (a, b, c), ki zadovoljijo a² + b² = c², npr. (3,4,5), (5,12,13). Obstaja neskončno število takih trojic; osnovni način generiranja jih daje Pitagorin parametrski izraz.
Razširitve: v več dimenzijah Pitagorov izrek postane formula za evklidsko razdaljo: v R^n je razdalja med točkama sqrt(x1² + x2² + ... + xn²). Prav tako izrek vodi do konceptov v linearni algebri in vektorjih.

Primeri uporabe

Izračun hipotenuse: če sta kraka dolga 3 in 4, potem je hipotenuza c = sqrt(3² + 4²) = 5 (primer 3-4-5).
Izračun kraka, če poznamo hipotenuzo in drugega kraka: če je c = 13 in a = 5, potem je b = sqrt(13² − 5²) = sqrt(169 − 25) = sqrt(144) = 12 (primer 5-12-13).
Uporabe v gradbeništvu, geodeziji, navigaciji, računalniški grafiki (izračun razdalj), fiziki in pri reševanju praktičnih problemov, kjer se pojavljajo pravokotni trikotniki.

Kratek zgodovinski pregled

Pitagorejci so izrek popularizirali in mu dali svojo povezavo z imenom Pitagora, vendar arheološki dokazi kažejo, da so znali posebne numerične primere že Babilonci (oko 1800 pr. n. št.) in da so indijski matematik Brahmagupta ter kitajski matematiki poznali sorodne izjave. Kljub zgodovinskemu izvoru je izrek temeljni rezultat evklidske geometrije in matematike nasploh.

Zaključek

Pitagorov izrek je ena najbolj osnovnih in uporabnih vezi v geometriji. Njegova enostavna oblika a² + b² = c² skriva bogato mrežo dokazov, številskih lastnosti in praktičnih uporabe, ki segajo od elementarnih izračunov do naprednih matematičnih in inženirskih področij.

Dokaz

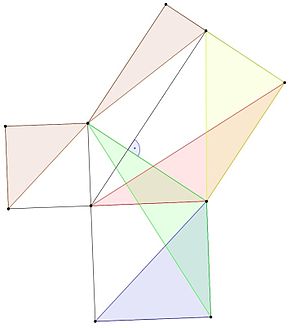
En dokaz Pitagorovega izreka je našel grški matematik Evdoks iz Knida.

V dokazu uporabimo tri leme:

Trikotniki z enako osnovo in višino imajo enako površino.
Trikotnik, ki ima enako osnovo in višino kot stranica kvadrata, ima enako površino kot polovica kvadrata.
Trikotniki z dvema skladnima stranicama in enim skladnim kotom so skladni in imajo enako površino.

Dokaz je:

Modri trikotnik ima enako površino kot zeleni trikotnik, saj ima enako osnovo in višino (lemma 1).
Zeleni in rdeči trikotnik imata dve stranici enaki stranicam istih kvadratov in kot, ki je enak ravnemu kotu (kotu 90 stopinj) plus kotu trikotnika, zato sta kongruentna in imata enako površino (lema 3).
Površini rdečega in rumenega trikotnika sta enaki, ker imata enako višino in osnovo (lema 1).
Površina modrega trikotnika je enaka površini površine rumenega trikotnika, ker

A b l u e = A g r e e e n = A r e d = A y e l l l o w {\displaystyle {\color {blue}A_{blue}}={\color {green}A_{green}}={\color {red}A_{red}}={\color {yellow}A_{yellow}}} ${\color {blue}A_{blue}}={\color {green}A_{green}}={\color {red}A_{red}}={\color {yellow}A_{yellow}}$

Rjavi trikotniki imajo iz istih razlogov enako površino.
Modri in rjavi kvadrat imata vsak polovico površine manjšega kvadrata. Vsota njunih površin je enaka polovici površine večjega kvadrata. Zaradi tega so polovice površin manjših kvadratov enake polovici površine večjega kvadrata, zato je njihova površina enaka površini večjega kvadrata.

Dokaz s podobnimi trikotniki

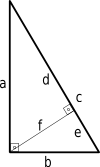
Še en dokaz Pitagorovega izreka lahko dobimo z uporabo podobnih trikotnikov.

d a = a c ⇒ d = a 2 c ( 1 ) {\displaystyle {\frac {d}{a}}={\frac {a}{c}}\quad \Rightarrow \quad d={\frac {a^{2}}{c}}\quad (1)} ${\frac {d}{a}}={\frac {a}{c}}\quad \Rightarrow \quad d={\frac {a^{2}}{c}}\quad (1)$

e/b = b/c => e = b^2/c (2)

Iz slike vemo, da je c = d + e {\displaystyle c=d+e\,\! } $c=d+e\,\!$ . Z zamenjavo enačb (1) in (2):

c = a 2 c + b 2 c {\displaystyle c={\frac {a^{2}}{c}}+{\frac {b^{2}}{c}}}} $c={\frac {a^{2}}{c}}+{\frac {b^{2}}{c}}$

Množenje s c:

c 2 = a 2 + b 2 . {\displaystyle c^{2}=a^{2}+b^{2}\,\!. } $c^{2}=a^{2}+b^{2}\,\!.$

Pitagorejski trojčki

Pitagorov trikotnik ali trikotnik so tri cela števila, ki ustrezajo enačbi a 2 + b 2 = c 2 {\displaystyle a^{2}+b^{2}=c^{2}} $a^{2}+b^{2}=c^{2}$ .

Trikotnik s stranicami 3, 4 in 5 je dobro znan primer. Če je a=3 in b=4, potem je 3 2 + 4 2 = 5 2 {\displaystyle 3^{2}+4^{2}=5^{2}} $3^{2}+4^{2}=5^{2}$ , ker je 9 + 16 = 25 {\displaystyle 9+16=25} $9+16=25$ . To lahko prikažemo tudi kot 3 2 + 4 2 = 5. {\displaystyle {\sqrt {3^{2}+4^{2}}}=5.} ${\sqrt {3^{2}+4^{2}}}=5.$

Trikotnik tri-štiri-pet deluje za vse mnogokratnike 3, 4 in 5. Z drugimi besedami, števila, kot so 6, 8, 10 ali 30, 40 in 50, so prav tako pitagorejski trojčki. Drug primer trikotnika je trikotnik 12-5-13, saj je 12 2 + 5 2 = 13 {\displaystyle {\sqrt {12^{2}+5^{2}}}=13}} ${\sqrt {12^{2}+5^{2}}}=13$ .

Pitagorov trojček, ki ni mnogokratnik drugih trojčkov, se imenuje primitivni pitagorov trojček. Vsako primitivno pitagorejsko trojico lahko najdemo z izrazom ( 2 m n , m 2 - n 2 , m 2 + n 2 ) {\displaystyle (2mn,m^{2}-n^{2},m^{2}+n^{2})} $(2mn,m^{2}-n^{2},m^{2}+n^{2})$ , vendar morajo biti izpolnjeni naslednji pogoji. Ti omejujejo vrednosti m {\displaystyle m} in n {\displaystyle n} .

m {\displaystyle m} in n {\displaystyle n} sta pozitivni celi števili
m {\displaystyle m} in n {\displaystyle n} nimata skupnih faktorjev, razen 1
m {\displaystyle m} in n {\displaystyle n} imata nasprotno pariteto. m {\displaystyle m} in n {\displaystyle n} imata nasprotno pariteto, kadar je m {\displaystyle m} sodo in n {\displaystyle n} liho ali m {\displaystyle m} liho in n {\displaystyle n} sodo.
m > n {\displaystyle m>n} .

Če so izpolnjeni vsi štirje pogoji, potem vrednosti m {\displaystyle m} in n {\displaystyle n} tvorita primitivni pitagorejski trojček.

m = 2 {\displaystyle m=2} $m=2$ in n = 1 {\displaystyle n=1} $n=1$ tvorita primitivni pitagorejski trojček. Vrednosti izpolnjujejo vse štiri pogoje. 2 m n = 2 × 2 × 1 = 4 {\displaystyle 2mn=2\times 2\times 1=4} $2mn=2\times 2\times 1=4$ , m 2 - n 2 = 2 2 - 1 2 = 4 - 1 = 3 {\displaystyle m^{2}-n^{2}=2^{2}-1^{2}=4-1=3} $m^{2}-n^{2}=2^{2}-1^{2}=4-1=3$ in m 2 + n 2 = 2 2 + 1 2 = 4 + 1 = 5 {\displaystyle m^{2}+n^{2}=2^{2}+1^{2}=4+1=5} $m^{2}+n^{2}=2^{2}+1^{2}=4+1=5$ tako je ustvarjena trojica ( 3 , 4 , 5 ) {\displaystyle (3,4,5)} $(3,4,5)$ .

Vprašanja in odgovori

V: Kaj je Pitagorov teorem?

O: Pitagorov teorem je izjava o stranicah pravokotnega trikotnika.

V: Kateri kot je v pravokotnem trikotniku vedno enak 90 stopinjam?

O: Eden od kotov v pravokotnem trikotniku je vedno enak 90 stopinjam, kar imenujemo pravi kot.

V: Kako se imenujeta dve stranici poleg pravega kota?

O: Dve stranici poleg pravega kota se imenujeta kraka.

V: Kako se imenuje stranica, ki je nasprotna pravemu kotu?

O: Stranica, ki je nasprotna pravemu kotu, se imenuje hipotenuza in je vedno najdaljša stranica.

V: Ali obstaja enačba za izračun te trditve?

O: Da, obstaja enačba za izračun tega izreka, ki pravi, da je "kvadrat dolžine hipotenuze enak vsoti kvadratov dolžin drugih dveh stranic".

V: Ali se vsi trikotniki s kotom 90 stopinj štejejo za "pravokotne" trikotnike?

O: Ne, vsi trikotniki s kotom 90 stopinj niso "pravilni" trikotniki; le tisti, pri katerih je ena stranica (hipotenuza) daljša od drugih dveh stranic in na koncu tvori kot 90 stopinj, se lahko uvrstijo med "prave" trikotnike.

Avtor

AlegsaOnline.com - Pitagorov izrek - Leandro Alegsa

Datum ustvarjanja: 20. junij 2021
Zadnja posodobitev: 30. avgust 2025

URL: https://sl.alegsaonline.com/art/80255