Neenakost (matematika): definicija, simboli in primeri
Izvedite vse o neenakostih v matematiki: definicije, simboli (<,>,≤,≥) in jasni primeri za hitro razumevanje ter reševanje nalog.
Neenakost je matematična izjava, s katero primerjamo dve količini ali izraza in trdimo, da je eden od njiju v nekem odnosu do drugega (manjši, večji ali enak). Neenakosti so osnovno orodje v algebri in analizi, uporabljamo pa jih tudi v vsakdanjih merjenjih, optimizaciji in statistiki.
- manjši od drugega (simbol: a < b —
; pomeni, da je a strogo manjši od b)
- večji od drugega (simbol: a > b —
; pomeni, da je a strogo večji od b)
- ni manjši od drugega (simbol: a ≥ b —
; pomeni, da je a bodisi večji bodisi enak b)
- ni večji od drugega (simbol: a ≤ b —
; pomeni, da je a bodisi manjši bodisi enak b)
- ni enak (simbol: a ≠ b; pomeni, da sta izraza različna)
Simboli in osnovni pomen
Glavni simboli so <, >, ≤, ≥ in ≠. = pomeni enakost, ki ni neenakost, vendar se v kombinaciji z neenakostmi pogosto uporablja pri sestavljanju pogojev (npr. a ≤ b pomeni a je manjši ali enak b).
Lastnosti neenakosti
- Tranzitivnost: če je a < b in b < c, potem a < c. Enako velja za ≤.
- Ohranjanje pri seštevanju/odštevanju: če je a < b, potem za poljubno realno c velja a + c < b + c.
- Ohranjanje pri množenju z pozitivnim številom: če je a < b in k > 0, potem ka < kb.
- Preobrat pri množenju z negativnim številom: če je a < b in k < 0, potem ka > kb (smer neenakosti se obrne).
- Deljenje z negativnim številom: pravilo obrata velja tudi pri deljenju — deljenje z negativnim številom obrne neenakost.
- Združevanje pogojev: neenakosti lahko povežemo z logičnim "in" ali "ali" — npr. 1 < x ≤ 5 pomeni, da je x med 1 in 5 (1 strogo manjši, 5 vključen).
Kako reševati neenakosti — primeri
Reševanje linearnih neenakosti poteka podobno kot pri enačbah, a pazimo na obrat smeri, če množimo ali delimo z negativnim številom.
- Primer 1: Rešimo 2x + 3 < 7.
Odštejemo 3: 2x < 4. Delimo z 2 (>0): x < 2. - Primer 2: Rešimo -3x > 6.
Delimo z -3 (negativno število) in obrnemo smer: x < -2. - Primer 3: 5 &le 2x + 1 < 11.
Odštejemo 1 v vseh delih: 4 &le 2x < 10. Delimo z 2: 2 &le x < 5.
Zapis z intervali in grafični prikaz
Neenakosti na realni osi pogosto zapišemo z intervali:
- a < x < b — odprt interval (a, b)
- a ≤ x ≤ b — zaprti interval [a, b]
- a ≤ x < b — mešani interval [a, b)
Na številčni premici zapišemo odprte konce kot prazne kroge in zaprte konce kot polne kroge; smer neenakosti (< ali >) kaže, na katero stran osi so sprejemljive vrednosti.
Uporaba
Neenakosti so ključne v reševanju problemov optimizacije (maksimizacija/minimizacija), v opisu domene funkcij, v oceni napak meritev in v statistiki (npr. znotraj zaupanja vrednosti). Razumevanje pravil za manipulacijo z neenakostmi je nujno pri reševanju enačb, sistemov neenakosti in pri analizi funkcij.
Če želite, lahko dodam več praktičnih primerov ali razložim reševanje kvadratnih neenakosti, neenakosti z absolutnimi vrednostmi ali sisteme neenakosti.
Delo z neenakostmi
O neenakosti v matematiki govorimo, ko dve rešitvi ali odgovora primerjamo z več kot ali manj kot. To je, kadar dve ali še več rešitev, ki se primerjata, nista enako veliki. Reševanje neenakosti pomeni iskanje njenih rešitev. Ko spremenljivki zamenjamo število in je trditev resnična, potem je to rešitev. Ko nadomestimo število s spremenljivko in izjava ni resnična, potem to število ni rešitev izjave.
Neenakost je iskanje rešitve za dano spremenljivko. To je iskanje relativnega reda množice. Neenakost ima veliko rešitev, vendar morate poiskati prave rešitve. Neenakost je reševanje realnih števil. Pravilen način branja neenakosti je od leve proti desni, tako kot pri drugih enačbah, le da imajo za vsako enačbo drugačna pravila.
Na primer x+4>12, pri čemer je x realno število. Najprej mora oseba poiskati x in vedeti, ali je to rešitev. Odgovor bo x>8 in to je resnična izjava. Ta izraz se nanaša na lokacijo x v množici realnih števil. Številska premica je eden od načinov za prikaz lokacije glede na vsa druga realna števila (glej sliko Neenakost 1).
.jpg)
Neenakost 1 To je rešitev za enačbo x+4>12
Različne vrste neenakosti
Obstaja pet različnih vrst neenakosti:
- Prva je linearna neenakost, ki je neenakost, ki razlikuje izraze z manj kot ali enako, manj kot ali večje kot ali enako, večje kot. To je tista, ki jo, če zamenjamo neenakost za zvezo enako, dobimo linearno enačbo.
- Druga je kombinacija neenačb, ki so, da bi zadovoljili neenačbi, morate imeti število v množicah rešitev, tako da bodo števila, ki zadoščajo neenačbam, vrednosti v križanju dveh množic rešitev.
- Tretja je neenakosti, ki vključujejo absolutne vrednosti, kar pomeni, da lahko vrednosti preoblikujemo kot kombinacije neenakosti, ki vključujejo absolutne vrednosti.
- Četrta se imenuje polinomske neenakosti in pomeni, da je zvezna, kar pomeni, da njeni grafi nimajo nobenih skokov ali prekinitev.
- Nenazadnje so to racionalne neenačbe, kar pomeni, da gre za obliko enega od polinomov, deljenega s polinomom. Z drugimi besedami, grafi racionalnih funkcij nimajo nobenih prelomov niti ne predstavljajo na ničlah imenovalca.
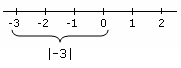
absolutna vrednost Primer, ki prikazuje absolutno vrednost
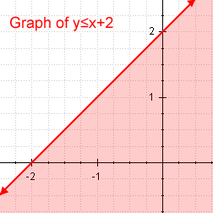
Linearna neenakost Primer linearne neenakosti
Štirje načini reševanja neenačb
Kvadratne enačbe lahko rešimo na štiri načine:
- Prvo pravilo je, da morate na obeh straneh sešteti ali odšteti enako število.
- Pravilo številka dve je, da morate premakniti strani in spremeniti položaj znaka neenakosti.
- Tretje pravilo je, da morate množiti.
- Četrto pravilo je, da isto pozitivno ali negativno število razdelimo na obe strani. Vendar jih lahko uporabite le pri lažjih problemih z neenakostmi.
Poleg tega sta za rešitev neenakosti potrebna dva koraka. Prvi je poenostavitev z uporabo recipročne vrednosti seštevanja ali odštevanja. Drugi korak je še večja poenostavitev z uporabo recipročne vrednosti množenja ali deljenja. Ko neenakost množite ali delite z negativnim številom, ne pozabite obrniti simbola neenakosti.

primer množenja neenakosti

Primer dodajanja neenačb.
Primeri reševanja neenačb
Neenakost je matematična izjava, ki pojasnjuje, da dve vrednosti nista enaki in različni. Enačba ab pomeni, da a ni enak b. Neenakost je enaka katerikoli enačbi, razlika je le v tem, da pri neenakosti ne uporabljamo znaka za enakost, temveč simbole. Neenakost b>a pomeni, da je b večji od a. Omejitve hitrosti, oznake in druge uporabljajo neenakost za izražanje.
Pri reševanju neenakosti mora imeti oseba resnično izjavo. Če neenakost delimo ali množimo z negativnim številom na obeh straneh, je izjava napačna. da bi bila izjava z negativnim številom pravilna, moramo obrniti simbol, da bi bila izjava pravilna. Kadar je število pozitivno, vam simbola ni treba obrniti. Pri neenakosti gre za to, da je izjava resnična.
Začni na primer z resnično izjavo -6y<-12. Ko obe stranici delimo z -6, dobimo rezultat y<2. V tej izjavi je treba obrniti simbol, da dobimo resnično izjavo, y>2 je pravilen odgovor. V številski premici (glej sliko Neenakost 2) zaprt osenčen krog opozarja, da je vključen v množico rešitev. Odprt krog označuje, da ni vključen v množico rešitev.
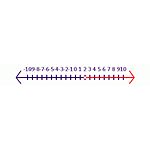
Neenakost 2 Rešitev za enačbo -6y<-12
Sorodne strani
- Enakost (matematika)
- Enačba
Vprašanja in odgovori
V: Kaj pomeni "a < b"?
O: Pomeni, da je a manjši od b.
V: Kaj pomeni "a > b"?
O: Pomeni, da je a večji od b.
V: Kaj pomeni "a ≥ b"?
O: Pomeni, da a ni manjši od b, torej da je večji ali enak b.
V: Kaj pomeni "a ≤ b"?
O: Pomeni, da a ni večji od b ali da je manjši ali enak b.
V: Kako lahko neenakost uporabimo v matematiki?
O: Neenakost lahko uporabimo za poimenovanje izjave, da je en izraz manjši, večji, ni manjši ali ni večji od drugega.
Iskati