Logaritem

Zgodovina

Logaritme so prvič uporabili v Indiji v 2. stoletju pred našim štetjem. V sodobnem času je logaritme prvi uporabil nemški matematik Michael Stifel (okoli leta 1487-1567). Leta 1544 je zapisal naslednji enačbi: q m q n = q m + n {\displaystyle q^{m}q^{n}=q^{m+n}} in q m q n = q m - n {\displaystyle {\tfrac {q^{m}}}{q^{n}}}=q^{m-n}} To je osnova za razumevanje logaritmov. Za Stifla morata biti m {\displaystyle m} in n {\displaystyle n} celi števili. John Napier (1550-1617) ni želel te omejitve in je želel razpon za eksponent.

Po Napierju logaritmi izražajo razmerja: a {\displaystyle a} ima enako razmerje kot b {\displaystyle b} in c {\displaystyle c} kot d {\displaystyle d}, če se razlika njunih logaritmov ujema. Matematično: log ( a ) - log ( b ) = log ( c ) - log ( d ) {\displaystyle \log(a)-\log(b)=\log(c)-\log(d)} . Sprva se je uporabljala osnova e (čeprav število še ni bilo poimenovano). Henry Briggs je predlagal uporabo 10 kot osnove za logaritme, ki so zelo uporabni v astronomiji.

John Napier se je ukvarjal z logaritmi

Povezava z eksponentnimi funkcijami

Logaritem pove, kakšen eksponent (ali moč) je potreben za določeno število, zato so logaritmi obratni (nasprotni) eksponentom.

Tako kot ima eksponentna funkcija tri dele, ima tudi logaritem tri dele. Trije deli logaritma so osnova, argument in odgovor (imenovan tudi moč).

To je eksponentna funkcija:

2 3 = 8 {\displaystyle 2^{3}=8\ }

V tej funkciji je osnova 2, argument 3, odgovor pa 8.

Ta eksponentna funkcija ima obratno vrednost, logaritem:

log 2 ( 8 ) = 3 {\displaystyle \log _{2}(8)=3\ }

V tem logaritmu je osnova 2, argument 8, odgovor pa 3.

Razlika do korenov

Seštevanje ima obratno operacijo: odštevanje. Tudi množenje ima eno obratno operacijo: deljenje. Zato je morda težko razumeti, zakaj ima eksponentnost pravzaprav dve obratni operaciji: Zakaj potrebujemo logaritem, če že imamo koren? To je zato, ker eksponentna operacija ni komutativna.

To ponazarja naslednji primer:

• Če imate x+2=3, lahko z odštevanjem ugotovite, da je x=3-2. Enako je, če imamo 2+x=3: prav tako dobimo x=3-2. To je zato, ker je x+2 enako kot 2+x.
• Če imamo x - 2=3, lahko z deljenjem ugotovimo, da je x= 3 2 {\textstyle {\frac {3}{2}}} . Enako je, če imamo 2 - x=3: prav tako dobimo x= 3 2 {\textstyle {\frac {3}{2}}} . To je zato, ker je x - 2 enako kot 2 - x.
• Če imate x²=3, potem uporabite (kvadratni) koren, da ugotovite x: Dobimo rezultat x = 3 {\textstyle {\sqrt {3}}}. Če pa imate 2^x =3, potem ne morete uporabiti korena za ugotovitev x. Namesto tega morate za ugotovitev x uporabiti (binarni) logaritem: Dobili boste rezultat x=log₂(3).
  To je zato, ker 2 ^xobičajno ni enako x (na ²primer 2 ⁵=32, vendar 5²=25).

Uporablja

Logaritmi lahko olajšajo množenje in deljenje velikih števil, saj je seštevanje logaritmov enako množenju, odštevanje logaritmov pa enako deljenju.

Preden so bili kalkulatorji priljubljeni in razširjeni, so ljudje za množenje in deljenje uporabljali logaritemske tabele v knjigah. Enake informacije v logaritemski tabeli so bile na voljo na drsniku, orodju, na katerem so bili zapisani logaritmi.

• Logaritemske spirale so v naravi pogoste. Primeri so lupina nautilusa ali razporeditev semen na sončnici.
• V kemiji je negativna vrednost logaritma aktivnosti hidronijevih ionov (H₃O ⁺, oblika H ⁺v vodi) v bazi 10 merilo, znano kot pH. Aktivnost hidronijevih ionov v nevtralni vodi je 10 ⁻⁷mol/L pri 25 °C, zato je pH 7. (To je posledica ravnotežne konstante, produkta koncentracije hidronijevih ionov in hidroksilnih ionov v vodnih raztopinah, ki je 10 ⁻¹⁴M ².)
• Richterjeva lestvica meri jakost potresa na logaritemski lestvici z osnovo 10.
• V astronomiji navidezna magnituda logaritemsko meri svetlost zvezd, saj se tudi oko na svetlost odziva logaritemsko.
• Glasbeni intervali se merijo logaritemsko kot poltoni. Interval med dvema tonoma v poltonih je logaritem osnove 2^1/12 frekvenčnega razmerja (ali enakovredno 12-krat logaritem osnove 2). Drobni poltoni se uporabljajo za neenake temperacije. Zlasti za merjenje odstopanj od enakomerno temperirane lestvice se intervali izražajo tudi v centih (stotinka enakomerno temperiranega poltona). Interval med dvema notama v centih je logaritem osnove 2^1/1200 frekvenčnega razmerja (ali 1200-krat logaritem osnove 2). V MIDI so note oštevilčene na poltonski lestvici (logaritemski absolutni nazivni ton s srednjim C pri 60). Za mikrotuning v drugih sistemih uglaševanja je opredeljena logaritemska lestvica, ki na združljiv način zapolnjuje razpone med poltoni enako temperirane lestvice. Ta lestvica ustreza številkam not za cele poltone. (glejte mikroladitev v MIDI).

Splošni logaritmi

Logaritme do osnove 10 imenujemo navadni logaritmi. Običajno so zapisani brez osnove. Na primer:

log ( 100 ) = 2 {\displaystyle \log(100)=2\ }

To pomeni:

10 2 = 100 {\displaystyle 10^{2}=100\ }

Naravni logaritmi

Logaritme do osnove e imenujemo naravni logaritmi. Število e je skoraj 2,71828 in se po matematiku Leonhardu Eulerju imenuje tudi Eulerjeva konstanta.

Naravni logaritmi imajo lahko simbole log e ( x ) {\displaystyle \log _{e}(x)\,} ali ln ( x ) {\displaystyle \ln(x)\,}

Nekateri avtorji raje uporabljajo naravne logaritme kot log ( x ) {\displaystyle \log(x)}, vendar to običajno omenijo na uvodnih straneh.

Pogoste osnove za logaritme

osnova	okrajšava	Komentarji
2	ld {\displaystyle \operatorname {ld} }	Zelo pogosto v računalništvu (binarno)
e	ln {\displaystyle \ln } ali preprosto log {\displaystyle \log }	Osnova je Eulerjeva konstanta e. To je najpogostejši logaritem, ki se uporablja v čisti matematiki.
10	log 10 {\displaystyle \log _{10}}ali log {\displaystyle \log } (včasih zapisano tudi kot lg {\displaystyle \lg } )	Uporablja se v nekaterih vedah, kot sta kemija in biologija.
katero koli število, n	log n {\displaystyle \log _{n}}	To je splošni način zapisovanja logaritmov

Lastnosti logaritmov

Logaritmi imajo številne lastnosti. Na primer:

Lastnosti iz definicije logaritma

Ta lastnost izhaja iz definicije logaritma:

log n ( n a ) = a {\displaystyle \log _{n}(n^{a})=a} Na primer

log 2 ( 2 3 ) = 3 {\displaystyle \log _{2}(2^{3})=3} in

log 2 ( 1 2 ) = - 1 {\displaystyle \log _{2}{\bigg (}{\frac {1}{2}}{\bigg )}=-1}, ker 1 2 = 2 - 1 {\displaystyle {\frac {1}{2}}=2^{-1}} .

Logaritem števila a
do osnove b je enak logaritmu števila a, deljenemu z logaritmom števila b. To pomeni,

log b ( a ) = log ( a ) log ( b ) {\displaystyle \log _{b}(a)={\frac {\log(a)}{\log(b)}}}

Na primer: a je 6, b pa 2. Z računali lahko dokažemo, da je to res ali vsaj zelo blizu:

log 2 ( 6 ) = log ( 6 ) log ( 2 ) {\displaystyle \log _{2}(6)={\frac {\log(6)}{\log(2)}}}

log 2 ( 6 ) ≈ 2,584962 {\displaystyle \log _{2}(6)\aprox 2,584962}

2,584962 ≈ 0,778151 0,301029 ≈ 2,584970 {\displaystyle 2,584962\approx {\frac {0,778151}{0,301029}}\approx 2,584970}

Naši rezultati so imeli majhno napako, vendar je bila ta posledica zaokroževanja številk.

Ker si naravni logaritem težko predstavljamo, ugotovimo, da je v obliki logaritma z osnovo deset:

ln ( x ) = log ( x ) log ( e ) ≈ log ( x ) 0,434294 {\displaystyle \ln(x)={\frac {\log(x)}{\log(e)}}\approx {\frac {\log(x)}{0,434294}}} Pri čemer je 0,434294 približek logaritma e.

 

Operacije znotraj argumentov logaritma

Logaritme, ki se pomnožijo znotraj svojega argumenta, lahko spremenimo na naslednji način:

log ( a b ) = log ( a ) + log ( b ) {\displaystyle \log(ab)=\log(a)+\log(b)}

Na primer,

log ( 1000 ) = log ( 10 ⋅ 10 ⋅ 10 ) = log ( 10 ) + log ( 10 ) + log ( 10 ) + log ( 10 ) = 1 + 1 + 1 = 3 {\displaystyle \log(1000)=\log(10\cdot 10\cdot 10)=\log(10)+\log(10)+\log(10)=1+1+1=3}

Enako velja za deljenje, vendar namesto seštevanja uporabljamo odštevanje, saj je to obratna operacija k množenju:

log ( a b ) = log ( a ) - log ( b ) {\displaystyle \log {\bigg (}{\frac {a}{b}}{\bigg )}=\log(a)-\log(b)}

Logaritemske tabele, drsna pravila in zgodovinske aplikacije

Pred elektronskimi računalniki so znanstveniki logaritme uporabljali vsak dan. Logaritmi so pomagali znanstvenikom in inženirjem na številnih področjih, na primer v astronomiji.

Pred računalniki je bila tabela logaritmov pomembno orodje. Leta 1617 je Henry Briggs natisnil prvo logaritemsko tabelo. To je bilo kmalu po Napierjevem osnovnem izumu. Pozneje so ljudje izdelovali tabele z boljšim obsegom in natančnostjo. Te tabele so navajale vrednosti log_b(x) in b ^xza poljubno število x v določenem območju, z določeno natančnostjo, za določeno osnovo b (običajno b = 10). Briggsova prva tabela je na primer vsebovala splošne logaritme za vsa cela števila v območju 1-1000 z natančnostjo 8 števk. Ker je funkcija f(x) = b ^xobratna funkcija log _b(x), jo imenujemo antilogaritem. Ljudje so te tabele uporabljali za množenje in deljenje števil. Uporabnik je na primer v tabeli poiskal logaritem za vsako od dveh pozitivnih števil. Če bi sešteval števila iz tabele, bi dobil logaritem produkta. Funkcija antilogaritma v tabeli bi nato našla produkt na podlagi njegovega logaritma.

Pri ročnih izračunih, ki zahtevajo natančnost, je iskanje dveh logaritmov, izračun njune vsote ali razlike in iskanje antilogaritma veliko hitrejše od izvajanja množenja na prejšnje načine.

Številne logaritemske tabele podajo logaritme tako, da ločeno podajo karakteristiko in mantiso x, torej celoštevilski in ulomni del log ₁₀(x). Karakteristika 10 - x je ena plus karakteristika x, njuna signifikanta pa sta enaka. To razširja področje uporabe logaritemskih tabel: če imamo tabelo z log ₁₀(x) za vsa cela števila x od 1 do 1000, je logaritem 3542 približan z

log 10 ( 3542 ) = log 10 ( 10 ⋅ 354,2 ) = 1 + log 10 ( 354,2 ) ≈ 1 + log 10 ( 354 ) . {\displaystyle \log _{10}(3542)=\log _{10}(10\cdot 354,2)=1+\log _{10}(354,2)\aprox 1+\log _{10}(354).\,}

Druga pomembna uporaba je bilo drsno pravilo, par logaritemsko razdeljenih lestvic, ki se je uporabljal za izračunavanje, kot je prikazano na sliki:

Številke so označene na drsnih lestvicah na razdaljah, ki so sorazmerne z razlikami med njihovimi logaritmi. Ustrezno premikanje zgornje lestvice pomeni mehansko seštevanje logaritmov. Če na primer razdaljo od 1 do 2 na spodnji lestvici prištejemo k razdalji od 1 do 3 na zgornji lestvici, dobimo produkt 6, ki ga odčitamo na spodnjem delu. Mnogi inženirji in znanstveniki so do sedemdesetih let 20. stoletja uporabljali drsna pravila. Znanstveniki lahko z drsnim pravilom delajo hitreje kot z logaritemsko tabelo.

Shematski prikaz drsnika. Začni z 2 na spodnji lestvici, dodaj razdaljo do 3 na zgornji lestvici, da dobiš produkt 6. Drsno pravilo deluje, ker je označeno tako, da je razdalja od 1 do x sorazmerna logaritmu x.


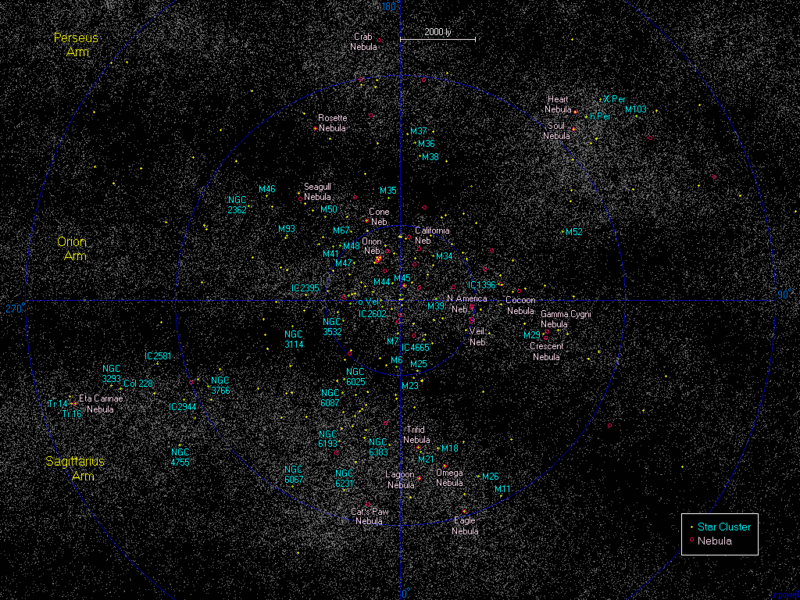
Najbližje meglice in zvezdne kopice (klikljiv zemljevid)