Algoritem – definicija, primeri, vrste in pomen v računalništvu

Primerjava algoritmov

Običajno obstaja več kot en način za rešitev problema. Obstaja lahko veliko različnih receptov za pripravo določene jedi, ki je videti različno, a je na koncu enakega okusa. Enako velja za algoritme. Vendar so nekateri od teh načinov boljši od drugih. Če recept zahteva veliko zapletenih sestavin, ki jih nimate, ni tako dober kot preprost recept. Ko obravnavamo algoritme kot način reševanja problemov, pogosto želimo vedeti, koliko časa bi računalnik potreboval za rešitev problema z uporabo določenega algoritma. Ko pišemo algoritme, želimo, da naš algoritem traja čim manj časa, da bi lahko problem rešili čim hitreje.

Pri kuhanju so nekateri recepti težji od drugih, ker je za njihovo izvedbo potrebnega več časa ali ker je treba spremljati več stvari. Enako velja za algoritme in algoritmi so boljši, če jih računalnik lažje izvede. Stvar, ki meri težavnost algoritma, se imenuje zapletenost. Ko se sprašujemo, kako zapleten je algoritem, pogosto želimo vedeti, koliko časa bo računalnik potreboval za rešitev problema, ki ga želimo, da ga reši.

Razvrščanje

To je primer algoritma za razvrščanje kart z barvami v kupčke iste barve:

1. Zberite vse karte.
2. Izberite karto iz svoje roke in si oglejte njeno barvo.
3. Če je na kupu že kup kart te barve, položite to karto na ta kup.
4. Če ni kupčka kart te barve, naredite nov kupček kart te barve.
5. Če je v roki še vedno karta, se vrnite na drugi korak.
6. Če v roki še vedno ni nobene karte, se karte razvrstijo. S tem ste končali.

Razvrščanje po številkah

To so primeri algoritmov za razvrščanje kupa kartic z več različnimi številkami, tako da so številke razvrščene po vrstnem redu.

Igralci imajo na začetku kup kart, ki še niso bile razvrščene.

Prvi algoritem

Ta algoritem gre skozi kup kart po eno karto naenkrat. Ta karta se primerja z naslednjo karto v kupu. Upoštevajte, da se ta položaj spremeni le v koraku 6. Ta algoritem se imenuje mehurčkasto razvrščanje. Je počasen.

1. Če je kup kart prazen ali vsebuje le eno karto, je razvrščen in končano.
2. Vzemite kup kart. Oglejte si prvo (zgornjo) karto v kupčku.
3. Karta, ki jo gledate, je karta A. Položaj, na katerem je trenutno karta A, je v kupu P.
4. Če v kupčku po karti A ni več kart, pojdite na korak 8.
5. Naslednja karta na kupčku je karta B.
6. Če ima karta B manjše število kot karta A, zamenjajte položaja kart A in B. Zapomnite si, da ste to storili. Ko zamenjate karte, ne spreminjajte položaja P.
7. Če je za položajem P na kupu še ena karta, jo poglejte; vrnite se na korak 3.
8. Če v zadnjem krogu niste zamenjali položaja nobene karte, ste končali; kup kart je razvrščen.
9. V nasprotnem primeru se vrnite na korak 2.

Primer po korakih

Vzemimo kup kart s številkami "5 1 4 2 8" in ga s tem algoritmom razvrstimo od najmanjše številke do največje. V vsakem koraku algoritem primerja elemente, zapisane v krepkem tisku. Vrh kupa kartic je na levi strani.

Prvi prehod:
( 5 1 4 2 8 ) → {\displaystyle \to } ( 1 5 5 4 2 8 ) Algoritem primerja prva dva elementa in ju zamenja.
( 1 5 4 2 8 ) → {\displaystyle \to } ( 1 4 5 2 8 )
( 1 4 5 2 8 ) → {\displaystyle \to } ( 1 4 2 5 8 )
( 1 4 2 5 8 ) → {\displaystyle \to } ( 1 4 2 5 8 ) Ti elementi so že urejeni, zato jih algoritem ne zamenja.
Drugi prehod:
( 1 4 2 5 8 ) → {\displaystyle \to } ( 1 4 2 5 8 )(
1 4 2 5 8 ) → {\displaystyle \to } ( 1 2 4 5 8 )
( 1 2 4 5 8 ) → {\displaystyle \to } ( 1 2 4 5 8 )
( 1 2 4 5 8 ) → {\displaystyle \to } ( 1 2 4 5 8 )
Zdaj je kup kart že razvrščen, vendar naš algoritem tega ne ve. Algoritem potrebuje en celoten prehod brez zamenjave, da bi vedel, da je urejen.
Tretji prehod:
( 1 2 4 5 8 ) → {\displaystyle \to } ( 1 2 4 5 8 )(
1 2 4 5 8 ) → {\displaystyle \to } ( 1 2 4 5 8 )
( 1 2 4 5 8 ) → {\displaystyle \to } ( 1 2 4 5 8 )
( 1 2 4 5 8 ) → {\displaystyle \to } ( 1 2 4 5 8 )
Na koncu je polje razvrščeno in algoritem se lahko ustavi.

Zgodovina

To je enostavno razumljiv algoritem za razvrščanje. Računalničarji so ga poimenovali Bubble sort, ker se manjši elementi dvignejo na vrh, pri čemer se njihov položaj v vsakem teku spremeni. Na žalost algoritem ni zelo dober, saj za razvrščanje potrebuje veliko časa (veliko prehodov skozi kup kart).

Drugi algoritem

Ta algoritem uporablja drugo zamisel. Včasih je rešitev problema težka, vendar lahko problem spremenimo tako, da je sestavljen iz enostavnejših problemov, ki jih je lažje rešiti. To se imenuje rekurzija. To je težje razumeti kot prvi primer, vendar bo dal boljši algoritem.

Osnovna ideja

1. Če v kupčku ni nobene karte ali je v njem samo ena karta, je kupček razvrščen in s tem ste končali.
2. Kup kart razdelite na dve približno enako veliki polovici. Če je število kart liho, bo na enem od obeh kupčkov ena karta več kot na drugem.
3. Vsako od obeh skladovnic razvrstite s tem algoritmom (za vsako skladovnico začnite pri 1. točki tega seznama.)
4. Združite oba razvrščena kupa, kot je opisano spodaj.
5. Rezultat je razvrščen kup kart. Končali ste.

Združevanje dveh skladov

To velja za dva kupčka kart. Ena od njih se imenuje A, druga B. Na začetku je tretja skladovnica prazna, imenovana C. Na koncu bo vsebovala rezultat.

1. Če je kupček A ali kupček B prazen, položite vse karte tistega kupčka, ki ni prazen, na vrh kupčka C; s tem ste končali, kupček C je rezultat združitve. (Opomba: vzemite celoten kupček in ga položite na kupček C; če boste to počeli kartico za kartico, se bo vrstni red spremenil in ne bo deloval tako, kot bi moral.)
2. Oglejte si zgornji karti kupčka A in kupčka B. Kartico z manjšo številko položite na vrh kupčka C. Če v kupčku C ni bilo nobene karte, bo zdaj v njem ena karta.
3. Če so v kupčku A ali B ostale še kakšne karte, se vrnite na korak 1 in jih razvrstite.

Zgodovina

John von Neumann je ta algoritem razvil leta 1945. Ni ga poimenoval razvrščanje po številkah, ampak Mergesort. V primerjavi z drugimi algoritmi je to zelo dober algoritem za razvrščanje.

Tretji algoritem

Prvi algoritem za razvrščanje kart potrebuje veliko več časa kot drugi, vendar ga je mogoče izboljšati. Pri razvrščanju z mehurčki lahko opazimo, da se karte z visokimi številkami precej hitro premaknejo z vrha kupa, karte z nizkimi številkami na dnu kupa pa potrebujejo veliko časa, da se dvignejo (premaknejo na vrh). Da bi izboljšali prvi algoritem, je tu naslednja zamisel:

Namesto da bi primerjali dve sosednji karti, na začetku izberete "posebno" karto. Vse druge karte se nato primerjajo z njo.

1. Začnemo s kupom A. Na začetku bosta še dva kupa B in C, ki ju bomo ustvarili pozneje.
2. Če v kupu A ni kart ali pa je v njem samo ena karta, smo z razvrščanjem končali.
3. Iz kupčka A se izbere karta, če je mogoče, naključno. To se imenuje pivot.
4. Vse preostale karte iz kupčka A se primerjajo s tem pivotom. Karte z manjšim številom gredo v kupček B, tiste z enakim ali večjim številom pa v kupček C.
5. Če so kakšne karte v kupčkih B ali C, je treba te kupčke razvrstiti z enakim algoritmom (Začni s pozicijo 1 tega seznama za oba kupčka B in C po vrsti.)
6. Opravljeno. V razvrščenem kupu kart je najprej razvrščeni kup B, nato pivot in nato razvrščeni kup C.

Zgodovina

Ta algoritem je leta 1960 razvil C. A. R. Hoare. Danes je eden od najbolj razširjenih algoritmov za razvrščanje. Imenuje se Quicksort.

Animacija, ki prikazuje delovanje razvrščanja v mehurčke


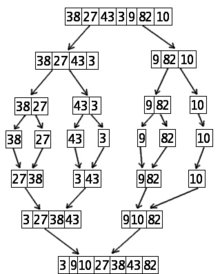
Razvrščanje 7 številk z drugim algoritmom za razvrščanje po številkah (Mergesort)


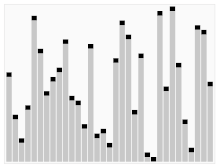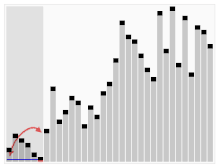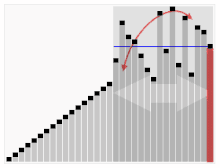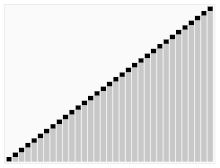
Tretji algoritem za razvrščanje kart. Element z rdečo črto je izbran kot pivot. Na začetku je to element povsem desno. Ta algoritem se imenuje Quicksort.

Sestavljanje algoritmov

Če imajo igralci karte z barvami in številkami, jih lahko razvrstijo po barvah in številkah, če izvedejo algoritem "razvrščanje po barvah", nato izvedejo algoritem "razvrščanje po številkah" za vsak barvni kupček in nato kupčke sestavijo skupaj.

Algoritmi razvrščanja po številkah so težji od algoritmov razvrščanja po barvah, saj bo morda treba korake večkrat ponoviti. Lahko bi rekli, da je razvrščanje po številkah bolj zapleteno.

Sorodne strani

• Evklidov algoritem je bil odkrit pred več kot 2000 leti. Z njim je mogoče najti največji skupni delitelj dveh števil.