AlegsaOnline.com

Fraktal: kaj je, kako deluje in praktične aplikacije

Fraktal: odkrijte, kaj je, kako deluje in praktične aplikacije — od narave do tehnologije. Vizualna lepota, matematične osnove in praktične uporabe v vsakdanjem svetu.

Avtor: Leandro Alegsa

14-12-2025

Fraktal je vsak vzorec, ki ob pogledu na sliko ustvari sliko, ki je ob povečavi še vedno enaka. Lahko jo razrežemo na dele, ki so videti kot manjša različica slike, s katero smo začeli. Besedo fraktal je leta 1975 iz latinske besede fractus, ki pomeni "zlomljen" ali "lomljen", ustvaril Benoît Mandelbrot. Preprost primer je drevo, ki se razveji v manjše veje, te pa v manjše veje in tako naprej. Fraktali niso le lepi, ampak imajo tudi veliko praktičnih aplikacij.

Kaj so fraktali in njihove ključne lastnosti

Fraktali so geometrijski ali matematični objekti, ki izstopajo predvsem po naslednjih lastnostih:

Samopodobnost: deli fraktala so podobni celoti — lahko je ta podobnost točna (npr. matematični fraktali) ali statistična (npr. naravni objekti).
Skalna invarianca: struktura se ohranja ob povečavi ali pomanjšavi znotraj določenih merilnih meja.
Fraktalna dimenzija: fraktali so pogosto "med" dimenzijami, npr. oblike z lastnostmi, ki jih ne moremo opisati samo z 1D, 2D ali 3D; zato uporabljamo pojme kot je Hausdorffova ali box-counting dimenzija.
Preprostost pravil, kompleksnost oblike: z zelo preprostimi iterativnimi ali rekurzivnimi pravili lahko nastanejo zelo kompleksne strukture.

Klasični primeri fraktalov

Med najbolj znanimi so matematični fraktali, ki so nastali v zgodovini matematike:

Kantorjev set
Kochova snežinka
Sierpinskijev trikotnik
Mandelbrotov množica in pripadajoče Julia-jeve množice

Ti primeri kažejo različne načine gradnje fraktalov: deterministični rekurzivni postopki, iterirane funkcijske sisteme in algoritme tipa "escape-time".

Kako nastanejo fraktali — osnovni algoritmi

Iterirani funkcijski sistemi (IFS): definiramo nabor geometrijskih transformacij in jih ponavljamo naključno ali v točnem zaporedju; rezultat je samopodobna množica.
Escape-time algoritmi: uporabljeni pri Mandelbrotovi in Julia množici; za vsako točko v kompleksni ravnini iterativno preverjamo, ali vrednosti "pobegnejo" v neskončno, in barvamo glede na hitrost pobega.
L-sistemi (Lindenmayer sistemi): formalni sistemi za opis rasti rastlin in vej, primerni za generiranje dreves in rastlinskih struktur.
Random/Noise metode: naključni fraktali, kot so Fractal Brownian Motion ali Perlinov šum, se uporabljajo za naraven videz oblakov, terena in tekstur.

Fraktali v naravi

Fraktalni vzorci se pogosto pojavljajo v naravi, čeprav običajno le na omejenem številu merilnih razponov. Primeri:

drevesne razvejitve in listne žile
obale in rečni sistemi
vzorci oblakov in gore
struktura krvnih žil in pljučnih bronhijev
nekatere vrste kristalnih in geoloških struktur

Praktične aplikacije

Fraktali niso le teoretični — uporabljajo se v številnih področjih:

Računalniška grafika in igre: proceduralna generacija terenov, oblakov, tekstur in vegetacije z uporabo fraktalov omogoča realističen videz z malo shranjenih podatkov.
Strojno inženirstvo (antene): fraktalne antene imajo večje pasovno območje in kompaktno obliko zaradi večjih obsevalnih lastnosti na različnih skalah.
Kompresija slik: metode, ki izkoriščajo samopodobnost, lahko stlačijo slike z manj podatki (fraktalna kompresija), čeprav niso več tako pogoste kot druge metode.
Analiza in modeliranje naravnih pojavov: geologija (razlika obalnih dolžin), meteorologija, ekologija in materialne znanosti uporabljajo fraktalne modele za opis kompleksnih struktur.
Medicina: analiza fraktalne dimenzije tkiv ali krvnih žil lahko pomaga pri preučevanju bolezni in rasti tumorjev.
Finančni trgi: nekateri modeli cenovnih nihanj in časovnih vrst uporabljajo fraktalno statistiko za opis heterogenih vzorcev volatilnosti.
Umetnost in oblikovanje: fraktalna umetnost je priljublena zaradi vizualne kompleksnosti in estetike, pa tudi pri generiranju logotipov, animacij in vizualnih efektov.

Merjenje fraktalnosti

Za kvantitativno opisovanje fraktalov uporabljamo pojme fraktalne dimenzije. Najpogosteje uporabljeni pristopi so:

Box-counting dimenzija: preštejemo število kvadratkov določene velikosti, ki pokrijejo množico, in analiziramo odvisnost od velikosti kvadratkov.
Hausdorffova dimenzija: teoretično strožji pojem, ki zahteva naprednejšo matematično opremo.

Omejitve in praktične opombe

Pomembno je poudariti, da so mnogi naravni objekti le približno fraktalni in to le znotraj omejenega razpona meril. Idealni matematični fraktali so neskončno ponavljajoči se, kar v realnem svetu ni mogoče. Prav tako je generiranje zelo podrobnih fraktalov računsko zahtevno in zahteva uravnotežen pristop med natančnostjo in zmogljivostjo.

Fraktali povezujejo matematiko, naravo in umetnost ter ponujajo močno orodje za modeliranje, analizo in ustvarjanje kompleksnih struktur iz preprostih pravil.

Mandelbrotova množica je znan primer fraktala.

Primeri

Obstaja veliko vrst fraktalov, ki so narejeni na najrazličnejše načine. Primer je trikotnik Sierpinskega, kjer je znotraj velikega trikotnika neskončno število majhnih trikotnikov. Drug primer je Mandelbrotova množica, poimenovana po Benoîtu Mandelbrotu. Sierpinksijev trikotnik je zgrajen s pomočjo vzorcev, Mandelbrotova množica pa temelji na enačbi.

Tudi v naravi je veliko naravnih primerov fraktalov, med drugim drevesa, snežinke, nekatere vrste zelenjave in obale.

Kochova krivulja

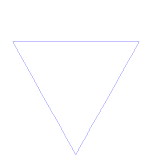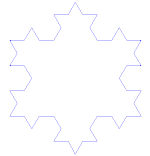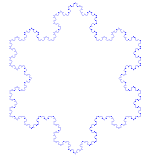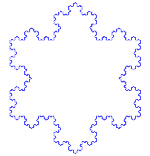
Kochova krivulja je preprost primer fraktala. Najprej začnemo z delom ravne črte, ki se imenuje odsek ravne črte. Premico razrežite na tri enako velike dele. Znebite se sredine teh kosov in vstavite zgornji del trikotnika s stranicami, ki so enako dolge kot izrezani kos. Zdaj imamo 4 odseke, ki se na koncih dotikajo. To, kar smo pravkar naredili s prvim odsekom, lahko zdaj naredimo z vsakim od štirih bitov. Enako lahko naredimo še enkrat in še enkrat z vsemi bitmi, ki smo jih dobili. Zdaj to počnemo v nedogled in poglejmo, kaj smo dobili.

Dolžina Kochove krivulje je neskončno, njena površina pa je enaka nič. To je precej nenavadno. Odsek črte (z dimenzijo 1) ima lahko dolžino 1, vendar ima površino 0. Kvadrat dolžine 1 in širine 1 (z dimenzijo 2) bo imel površino 1 in dolžino neskončno.

Dimenzija podobnosti

Tako se zdi, da je Kochova krivulja večja od nečesa z razsežnostjo 1 in manjša od nečesa z razsežnostjo 2. Namen dimenzije podobnosti je podati dimenzijo, ki daje boljšo predstavo o dolžini ali površini fraktalov. Za Kochovo krivuljo torej želimo dimenzijo med 1 in 2.

Kochovo krivuljo lahko razrežemo na štiri dele, od katerih je vsak 1 3 {\displaystyle {\frac {1}{3}}} ${\frac {1}{3}}$ velikosti izvirnika. Število kosov, na katere lahko razrežemo fraktal, imenujemo N {\displaystyle N} $N$ , razliko v velikosti pa B {\displaystyle B} $B$ . Ta dva podatka vstavimo v enačbo:

log N - log B {\displaystyle {\frac {\log N}{-\log B}}} ${\frac {\log N}{-\log B}}$

Pri čemer je log {\displaystyle \log } $\log$ logaritem števila. To število je Hausdorffova dimenzija fraktala. Pri Kochovi krivulji je to log 4 - log 1 3 = 1,2619... {\displaystyle {\frac {\log 4}{-\log {\frac {1}{3}}}}=1,2619... } ${\frac {\log 4}{-\log {\frac {1}{3}}}}=1.2619...$ , kot smo želeli.

Kochova krivulja je ena najpreprostejših fraktalnih oblik, zato je njeno dimenzijo enostavno določiti. Njena dimenzija podobnosti in Hausdorffova dimenzija sta enaki. To ne velja za bolj zapletene fraktale.

Kochova snežinka

Kochova snežinka (ali Kochova zvezda) je enaka Kochovi krivulji, le da se začne z enakostraničnim trikotnikom namesto z odsekom črte.

Uporablja

Fraktali se pogosto uporabljajo, npr. v biologiji (pljuča, ledvice, variabilnost srčnega utripa itd.), pri potresih, v financah, kjer so povezani s t. i. porazdelitvami težkih repov, in v fiziki. To kaže, da bi bilo treba fraktale preučevati, da bi razumeli, zakaj so fraktali v naravi tako pogosti.

Nekateri fraktali obstajajo le iz umetniških razlogov, drugi pa so zelo uporabni. Fraktali so zelo učinkovite oblike za radijske antene in se uporabljajo v računalniških čipih za učinkovito povezovanje vseh komponent. Tudi obalne črte si lahko predstavljamo kot fraktale.

Vprašanja in odgovori

V: Kaj je fraktal?

O: Fraktal je vsak vzorec, ki ob pogledu na sliko ustvari sliko, ki bo še vedno enaka, če jo povečamo.

V: Kdo je zaslužen za nastanek izraza "fraktal"?

O: Benoît Mandelbrot je zaslužen, da je leta 1975 skoval izraz "fraktal".

V: Kakšna je etimologija besede "fraktal"?

O: Beseda "fraktal" izhaja iz latinske besede "fractus", ki pomeni "zlomljen" ali "lomljen".

V: Ali lahko fraktale razrežemo na dele?

O: Da, fraktale je mogoče razrezati na dele, ki so videti kot manjša različica slike, s katero so začeli.

V: Ali lahko navedete primer fraktala?

O: Preprost primer fraktala je drevo, ki se razveji v manjše veje, te pa v manjše veje in tako naprej.

V: Kako se fraktali uporabljajo v praksi?

O: Fraktali imajo veliko praktičnih aplikacij, na primer v računalniški grafiki, medicini, fiziki in financah.

V: Zakaj so fraktali pomembni?

O: Fraktali so pomembni, ker nam lahko pomagajo razumeti zapletene naravne pojave ter ustvariti natančnejše modele in simulacije.