Dimenzije: definicija in uporaba v matematiki, fiziki in vsakdanjem življenju
Dimenzije: definicija in uporaba v matematiki, fiziki in vsakdanjem življenju. Preprosti primeri, merjenja (1D–4D) in praktične razlage za vsakdanjo rabo.
Dimenzije so način, kako vidimo, merimo in doživljamo naš svet. Z uporabo gor in dol, od desne proti levi, od zadaj proti spredaj, vroče in hladno, kako težko in kako dolgo ter naprednejših pojmov iz matematike in fizike. Eden od načinov za opredelitev razsežnosti je, da si ogledamo stopnje svobode ali način, kako se lahko predmet giblje v določenem prostoru. Obstajajo različni koncepti ali načini uporabe izraza dimenzija, prav tako pa obstajajo različne opredelitve. Ni definicije, ki bi zadovoljila vse koncepte.
Kaj pomeni dimenzija?
Poenostavljeno je dimenzija število neodvisnih smeri ali parametrov, potrebnih za opis položaja ali stanja predmeta. V vsakdanjem jeziku se dimenzije pogosto nanašajo na dolžino, širino in višino, toda v znanosti in matematiki ima pojem širši pomen in različne nianse glede na kontekst.
Dimenzije v matematiki
V vektorskem prostoru (vektor je odprta zaključena črta) je dimenzija enaka kardinalnosti ali številu smeri vektorjev ali črt. Pogosteje rečeno, dimenzija v vektorskem prostoru pomeni velikost baze — torej največje število linearno neodvisnih vektorjev, ki tvorijo osnovo prostora. Na primer prostor R^n ima dimenzijo n: to pomeni, da za določitev položaja potrebujemo n koordinat (x1, x2, ..., xn).
Matematiki pa razlikujejo še druge vrste dimenzij: topološko dimenzijo (kako se prostor obnaša lokalno), Hausdorffovo ali fraktalno dimenzijo (ki lahko ni celo število za kompleksne, samopodobne množice), ter dimenzije v algebraičnih ali kombinatoričnih konstrukcijah. Vsaka od teh ima svoje definicije in uporabne lastnosti.
Dimenzije v fiziki
V fiziki se dimenzije uporabljajo na več ravneh. Ena je geometrijska — pri opisovanju položaja v prostoru uporabljamo običajno tri prostorske dimenzije, ki jih imenujemo dolžina, širina in globina
Matematiki ta koncept imenujejo evklidski prostor.
Druga pomembna uporaba v fiziki so fizične dimenzije (npr. dolžina [L], masa [M], čas [T], električni tok [I] itd.), ki se uporabljajo v dinamičnih enačbah in pri dimenzijski analizi. Dimenzijska analiza pomaga preveriti smiselnost enačb, pretvoriti enote in predvideti, kako se spremenljivke med seboj razmeroma vplivajo.
V teorijah relativnosti in sodobni fiziki se včasih za prikaz položaja dogodka v času in prostoru uporablja četrta (4D) dimenzija, čas. V tem okviru se prostor in čas združita v štiridimenzionalno prostor–časovno strukturo, kjer imajo dogodki koordinate (x, y, z, t).
Merjenje položaja in koordinate
Dimenzije se lahko uporabljajo tudi za merjenje položaja. Razdaljo do položaja od začetnega mesta lahko merimo v smeri dolžine, širine in višine. Te razdalje so merilo položaja in jih običajno zapišemo kot nabor koordinat. V praksi to pomeni, da za opis točke v 3D potrebujemo tri številske vrednosti (npr. x, y, z).
Dimenzije v vsakdanjem življenju in tehnologiji
V vsakdanjem življenju dimenzije uporabljamo pri merjenju predmetov (npr. dolžina mize, višina omare), pri opisu oblik in prostorskih razmer ter pri načrtovanju in izdelavi. V računalništvu in podatkovnih znanostih pogosto govorimo o visokodimenzionalnih podatkovnih prostorih, kjer ima vsak primer veliko lastnosti (dimenzij) — npr. slika, predstavljena z množico pikslov, ima dimenzijo enako številu pikslov.
Druge uporabe in omejitve pojma
Ker obstaja več definicij dimenzije, je pomembno vedeti, kateri pomen se uporablja v konkretni situaciji. Na primer:
- Geometrijska dimenzija: število koordinat, potrebnih za opis položaja.
- Linearna algebra: dimenzija vektorskega prostora (velikost baze).
- Fizikalne dimenzije: osnovne količine kot so dolžina, masa, čas, ki določajo obliko enačb.
- Fraktalna dimenzija: lahko ni celo število in opisuje kompleksnost samopodobnih struktur.
Zaključek
Dimenzija je temeljni pojem, ki povezuje geometrijo, algebra, fiziko in vsakdanje merjenje. Čeprav se definicije razlikujejo glede na področje, pri vseh velja osnovna ideja: dimenzija pove, koliko neodvisnih smeri ali parametrov potrebujemo za opis nečesa. Razumevanje različnih vrst dimenzij in njihove uporabe omogoča pravilno modeliranje, merjenje in interpretacijo pojavov v znanosti in vsakdanjem življenju.
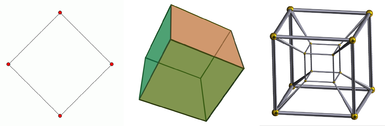
Od leve proti desni: kvadrat, kocka in teserakt. Kvadrat je dvodimenzionalni predmet, kocka je tridimenzionalni predmet, teserakt pa je štiridimenzionalni predmet. Enodimenzionalni predmet je samo črta. Podana je projekcija kocke, saj jo gledamo na dvodimenzionalnem zaslonu. Enako velja za teserakt, ki ga lahko dodatno prikažemo le kot projekcijo tudi v tridimenzionalnem prostoru.

Diagram prvih štirih prostorskih dimenzij.
Druge dimenzije
V sodobni znanosti ljudje uporabljajo druge dimenzije. Dimenzije, kot sta temperatura in teža, se lahko uporabljajo za prikaz položaja nečesa v manj preprostih prostorih. Znanstveniki te dimenzije preučujejo z dimenzijsko analizo.
Matematiki prav tako uporabljajo dimenzije. V matematiki so dimenzije bolj splošne. Dimenzije v matematiki morda ne merijo stvari v svetu. Pravila za izvajanje aritmetike z razsežnostmi v matematiki so lahko drugačna od običajnih aritmetičnih pravil.
Dimenzije in vektorji
Vektorji se uporabljajo za prikazovanje razdalj in smeri. Vektorji se pogosto uporabljajo v tehniki in znanosti, včasih pa tudi v matematiki.
Vektor je seznam števil. Za vsako dimenzijo je eno število. Za vektorje obstajajo aritmetična pravila.
Če na primer Jane želi izvedeti položaj Sally, lahko Sally poda Jane vektor, ki prikazuje položaj. Če sta Jane in Sally v svetu, obstajajo tri razsežnosti. Zato Sally da Janeu seznam treh številk, s katerimi prikaže svoj položaj. Tri številke v vektorju, ki ga Sally da Jane, so lahko naslednje:
- Sallyina razdalja severno od Jane
- Razdalja Sally vzhodno od Jane
- višina Sally nad Jane
Vprašanja in odgovori
V: Kaj je dimenzija?
A: Dimenzija je način merjenja, gledanja in doživljanja sveta z uporabo pojmov, kot so gor in dol, od desne proti levi, od zadaj proti spredaj, vroče in hladno, kako težko in kako dolgo. Opredelimo jo lahko tudi kot stopnjo svobode ali način, kako se lahko predmet giblje v določenem prostoru.
V: Kako matematiki opredeljujejo evklidski prostor?
O: Matematiki opredeljujejo evklidski prostor kot prostor, ki ga določajo tri dimenzije, ki se običajno imenujejo dolžina, širina in globina.
V: Kakšno je število vektorjev v vektorskem prostoru?
O: Število vektorjev v vektorskem prostoru je enako kardinalnosti (ali številu vektorjev) njegove osnovne množice.
V: Koliko dimenzij uporabljamo za merjenje položaja?
O: Za merjenje položaja se uporabljajo tri dimenzije (dolžina, širina in višina). V nekaterih primerih se lahko za prikaz položaja dogodka v času in prostoru uporabi četrta (4D) dimenzija - čas.
V: Kaj pomeni dim(V)?
O: Dim(V) se nanaša na dimenzijo V, ki je enaka kardinalnosti (ali številu vektorjev) njegove osnovne množice ali enaka številu smeri premic, ki jih ima.
V: Ali obstaja ena definicija, ki ustreza vsem konceptom, povezanim z dimenzijami?
O: Ne, ni ene same definicije, ki bi zadovoljila vse koncepte, povezane z dimenzijami.
Iskati