Algebra: definicija, osnovni pojmi, enačbe, funkcije in uporaba

Zgodovina

Zgodnje oblike algebre so razvili Babilonci in grški geometri, kot je bil Hero iz Aleksandrije. Vendar je beseda "algebra" latinska oblika arabske besede Al-Jabr ("litje") in izhaja iz matematične knjige Al-Maqala fi Hisab-al Jabr wa-al-Muqabilah ("Esej o računanju litja in enačbe"), ki jo je v 9. stoletju napisal perzijski matematik Muhammad ibn Mūsā al-Khwārizmī, musliman, rojen v Khwarizmu v Uzbekistanu. V letih 813-833 n. št. je živel pod vodstvom Al-Ma'muna v Bagdadu v Iraku, umrl pa okoli leta 840 n. št. Knjiga je bila prinesena v Evropo in prevedena v latinščino v 12. stoletju. Knjiga je nato dobila ime "algebra". (Končnica matematikovega imena al-Khwarizmi je bila spremenjena v besedo, ki jo je bilo lažje izgovoriti v latinščini, in je postala angleška beseda algorithm).

Primeri

Tukaj je preprost primer problema algebre:

Sue ima 12 bonbonov, Ann pa 24 bonbonov. Odločita se, da si jih bosta razdelili, tako da bosta imeli enako število bonbonov. Koliko bonbonov bo imela vsaka od njiju?

S temi koraki lahko rešite težavo:

1. Da bi imela enako število bonbonov, mora Ann nekaj bonbonov dati Sue. Naj x predstavlja število bonbonov, ki jih Ann da Sue.
2. Sueini bonboni plus x morajo biti enaki Anninim bonbonom minus x. To zapišemo kot: 12 + x = 24 - x
3. Od obeh strani enačbe odštejte 12. Tako dobimo: x = 12 - x. (Kar se zgodi na eni strani enačbe, se mora zgoditi tudi na drugi strani, da je enačba še vedno resnična. V tem primeru je torej, ko smo od obeh strani odšteli 12, nastala srednja stopnja 12 + x - 12 = 24 - x - 12. Ko je oseba s tem zadovoljna, srednjega koraka ne zapiše.)
4. Na obe strani enačbe dodajte x. Tako dobimo: 2x = 12
5. Obe strani enačbe delimo z 2. Tako dobimo x = 6. Odgovor je šest. Če Ann da Sue 6 bonbonov, bosta imeli enako število bonbonov.
6. To preverite tako, da v prvotno enačbo, kjer je bil x, vstavite 6: 12 + 6 = 24 - 6
7. Tako dobimo 18=18, kar je res. Vsak od njiju ima zdaj 18 bonbonov.

Z vajo lahko algebro uporabimo, ko se soočimo s problemom, ki ga je pretežko rešiti na drug način. Pri problemih, kot so gradnja avtoceste, načrtovanje mobilnega telefona ali iskanje zdravila za bolezen, je potrebna algebra.

Pisanje algebre

Tako kot v večini matematike se dodajanje z k y (ali y plus z) zapiše kot y + z. Odštevanje z od y (ali y minus z) se zapiše kot y - z. Deljenje y z z (ali y nad z: y z {\displaystyle y \over z} ) se zapiše kot y ÷ z ali y/z. pogosteje se uporablja y/z.

V algebri lahko množenje y z z (ali y krat z) zapišemo na štiri načine: y × z, y * z, y-z ali samo yz. Simbol za množenje "×" se običajno ne uporablja, ker je preveč podoben črki x, ki se pogosto uporablja kot spremenljivka. Pri množenju večjega izraza lahko uporabimo tudi oklepaje: y (z+1).

Ko v algebri množimo število in črko, zapišemo število pred črko: 5 × y = 5y. Kadar je število 1, 1 ne pišemo, ker je 1 krat katero koli število to število (1 × y = y), zato ga ne potrebujemo.

Kot dodatno opombo naj povem, da v algebri ni treba uporabljati črk x ali y. Spremenljivke so le simboli, ki pomenijo neko neznano število ali vrednost, zato lahko uporabite katero koli spremenljivko, vendar sta x in y najpogostejši.

Funkcije in grafi

Pomemben del algebre je preučevanje funkcij, saj se funkcije pogosto pojavljajo v enačbah, ki jih poskušamo rešiti. Funkcija je kot stroj, v katerega lahko vstavimo število (ali števila) in iz njega dobimo določeno število (ali števila). Pri uporabi funkcij so lahko grafi močno orodje, ki nam pomaga pri preučevanju rešitev enačb.

Graf je slika, na kateri so prikazane vse vrednosti spremenljivk, zaradi katerih je enačba ali neenačba resnična. Običajno je to enostavno narediti, če imamo le eno ali dve spremenljivki. Graf je pogosto premica, in če se premica ne upogiba ali ne poteka naravnost navzgor in navzdol, jo lahko opišemo z osnovno formulo y = mx + b. Spremenljivka b je y-intercept grafa (kjer premica preseka navpično os), m pa je naklon ali strmina premice. Ta formula velja za koordinate grafa, kjer je vsaka točka na premici zapisana (x, y).

V nekaterih matematičnih problemih, kot je enačba premice, je lahko več kot ena spremenljivka (v tem primeru x in y). Za iskanje točk na premici spremenimo eno spremenljivko. Spremenljivka, ki jo spremenimo, se imenuje "neodvisna" spremenljivka. Nato se izvede matematika, da se dobi število. Število, ki ga dobimo, se imenuje "odvisna" spremenljivka. Največkrat je neodvisna spremenljivka zapisana kot x, odvisna spremenljivka pa kot y, na primer y = 3x + 1. To se pogosto prikaže na grafu z osjo x (levo in desno) in osjo y (navzgor in navzdol). Zapišemo ga lahko tudi v obliki funkcije: f(x) = 3x + 1. V tem primeru bi lahko za x vnesli 5 in dobili y = 16. Če bi za x vstavili 2, bi dobili y = 7. Če bi za x vnesli 0, bi dobili y = 1. Tako bi skozi točke (5,16), (2,7) in (0,1) potekala premica, kot je razvidno iz grafa na desni.

Če ima x moč 1, je to premica. Če je kvadrat ali kakšna druga moč, je krivulja. Če uporablja neenakost (< ali > ), je običajno del grafa zasenčen, bodisi nad ali pod premico.

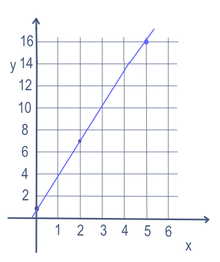
Linearna enačba za y=3x+1

Pravila algebre

V algebri obstaja nekaj pravil, ki jih lahko uporabimo za boljše razumevanje enačb. Imenujemo jih pravila algebre. Čeprav se ta pravila morda zdijo nesmiselna ali očitna, je pametno razumeti, da te lastnosti ne veljajo v vseh vejah matematike. Zato bo koristno vedeti, kako so ta aksiomatska pravila deklarirana, preden jih vzamemo za samoumevna. Preden preidemo k pravilom, razmislimo o dveh definicijah, ki ju bomo podali.

1. Nasprotje - nasprotno od {\displaystyle a} je - a {\displaystyle -a} .
2. Vzajemnost - vzajemnost a {\displaystyle a} je 1 a {\displaystyle {\frac {1}{a}}} .

Pravila

Komutativna lastnost seštevanja

"Komutativni" pomeni, da ima funkcija enak rezultat, če zamenjamo števila. Z drugimi besedami, vrstni red členov v enačbi ni pomemben. Kadar je operator dveh izrazov seštevanje, velja 'komutativna lastnost seštevanja'. V algebrskem jeziku to pomeni a + b = b + a {\displaystyle a+b=b+a} .

Upoštevajte, da to ne velja za odštevanje! (tj. a - b ≠ b - a {\displaystyle a-b\neq b-a} )

Komutativna lastnost množenja

Kadar je operator dveh izrazov množenje, velja "komutativna lastnost množenja". V algebrskem smislu to pomeni a ⋅ b = b ⋅ a {\displaystyle a\cdot b=b\cdot a} .

Upoštevajte, da to ne velja za delitev! (tj. a b ≠ b a {\displaystyle {\frac {a}{b}}}neq {\frac {b}{a}}}}) ko a ≠ b {\displaystyle a\neq b} )

Asociativna lastnost seštevanja

"Asociativni" se nanaša na združevanje števil. Asociativna lastnost seštevanja pomeni, da pri seštevanju treh ali več členov ni pomembno, kako so ti členi razvrščeni v skupine. Algebrsko to pomeni a + ( b + c ) = ( a + b ) + c {\displaystyle a+(b+c)=(a+b)+c} . Upoštevajte, da to ne velja za odštevanje, npr. 1 = 0 - ( 0 - 1 ) ≠ ( 0 - 0 ) - 1 = - 1 {\displaystyle 1=0-(0-1)\neq (0-0)-1=-1} (glej distributivno lastnost).

Asociativna lastnost množenja

Asociativna lastnost množenja pomeni, da pri množenju treh ali več členov ni pomembno, kako so ti členi razvrščeni v skupine. Algebraično to pomeni a ⋅ ( b ⋅ c ) = ( a ⋅ b ) ⋅ c {\displaystyle a\cdot (b\cdot c)=(a\cdot b)\cdot c} . Upoštevajte, da to ne velja za deljenje, npr. 2 = 1 / ( 1 / 2 ) ≠ ( 1 / 1 ) / 2 = 1 / 2 {\displaystyle 2=1/(1/2)\neq (1/1)/2=1/2} .

Distributivna lastnost

Distributivna lastnost pravi, da je množenje števila z drugim izrazom mogoče porazdeliti. Na primer: a ⋅ ( b + c ) = a b + a c {\displaystyle a\cdot (b+c)=ab+ac} . (Ne zamenjujte tega z asociativnimi lastnostmi! Na primer, a ⋅ ( b + c ) ≠ ( a ⋅ b ) + c {\displaystyle a\cdot (b+c)\neq (a\cdot b)+c} .)

Lastnost aditivne identitete

"Identiteta" se nanaša na lastnost števila, da je enako samemu sebi. Z drugimi besedami, obstaja operacija dveh števil, ki je enaka spremenljivki vsote. Lastnost aditivne identitete pravi, da je vsota poljubnega števila in 0 enako temu številu: a + 0 = a {\displaystyle a+0=a} . To velja tudi za odštevanje: a - 0 = a {\displaystyle a-0=a} .

Lastnost multiplikativne identitete

Lastnost multiplikativne identitete pravi, da je produkt poljubnega števila in 1 to število: a ⋅ 1 = a {\displaystyle a\cdot 1=a} . To velja tudi za deljenje: a 1 = a {\displaystyle {\frac {a}{1}}=a} .

Lastnost aditivne inverzije

Lastnost aditivne inverzije je nekako nasprotje lastnosti aditivne identitete. Če je operacija vsota števila in njegovega nasprotja in je enaka 0, je ta operacija veljavna algebrska operacija. Algebrsko je to naslednje: a - a = 0 {\displaystyle a-a=0} . Aditivna inverzija števila 1 je (-1).

Multiplikativna obratna lastnost

Multiplikativna inverzna lastnost pomeni, da če je operacija produkt števila in njegove recipročne vrednosti in je enaka 1, je ta operacija veljavna algebrska operacija. Algebraično je to naslednje: a a = 1 {\displaystyle {\frac {a}{a}}=1} . Multiplikativna inverzija 2 je 1/2.

Napredna algebra

Poleg "elementarne algebre" ali osnovne algebre obstajajo tudi napredne oblike algebre, ki se poučujejo na fakultetah in univerzah, kot so abstraktna algebra, linearna algebra in univerzalna algebra. To vključuje tudi uporabo matrike za reševanje več linearnih enačb naenkrat. Abstraktna algebra je študij stvari, ki jih najdemo v enačbah, in presega števila ter se ukvarja z bolj abstraktnimi skupinami števil.

Veliko matematičnih problemov se nanaša na fiziko in tehniko. V mnogih od teh fizikalnih problemov je čas spremenljivka. Čas uporablja črko t. Z uporabo osnovnih idej algebre lahko matematični problem zmanjšamo na najpreprostejšo obliko in tako lažje rešujemo težke probleme. Energija je e, sila je f, masa je m, pospešek je a, svetlobna hitrost pa je včasih c. To se uporablja v nekaterih znanih enačbah, kot sta f = ma in e=mc^2 (čeprav je bila za zadnjo enačbo potrebna bolj zapletena matematika zunaj algebre).

Sorodne strani

• Seznam matematičnih tem
• Vrstni red operacij
• Parabola
• Sistem računalniške algebre