Osnove algebre: definicija, enačbe in praktična uporaba

Osnove algebre: jasne definicije, praktične enačbe in uporabe v šoli, znanosti in poslu — naučite se reševati enačbe, posploševati pravila in razumeti funkcionalne odnose.

Avtor: Leandro Alegsa

17-12-2025 22:30

Osnovna algebra je najosnovnejša oblika algebre, ki se je učijo učenci. Pogosto je za aritmetiko eno od naslednjih področij matematike, ki se ga učenci učijo. Medtem ko se pri aritmetiki pojavljajo samo števila in operatorji, kot so +, -, × in ÷, se pri algebri spremenljivke (kot so a, x, y) uporabljajo za označevanje števil. To je koristno, ker:

Z njo lahko rešujejo probleme o "neznanih" številkah. To pomeni spoznavanje enačb in njihovo reševanje (na primer: "Poišči število x, pri katerem je 3 x + 1 = 10 {\displaystyle 3x+1=10} $3x+1=10$ ").
Omogoča posplošitev pravil iz aritmetike. Nekateri učenci razumejo, da je 3 + 4 = 4 + 3 {\displaystyle 3+4=4+3}. $3+4=4+3$ , pomaga dokazati, da a + b = b + a {\displaystyle a+b=b+a} za vse a in b. Zaradi tega je algebra dober korak k učenju abstrakcije (učenje splošnih idej iz številnih primerov).
Pomaga ljudem razumeti in oblikovati funkcionalne odnose (včasih imenovane tudi vzroki in posledice). Primer tega je "če se proda x vstopnic, bo dobiček 3 x - 10 {\displaystyle 3x-10} $3x-10$ dolarjev".

Ti trije sklopi so glavni poudarki osnovne algebre. Elementarna algebra se pogosto uporablja pri številnih drugih predmetih, kot so znanost, poslovanje in gradbeništvo. Abstraktno algebro, ki je veliko bolj napredna tema, se običajno poučuje pozno na fakulteti.

Kaj pomeni rešiti enačbo?

Reševanje enačbe pomeni najti vrednost spremenljivke, ki naredi enačbo resnično. Na primer, za enačbo 3x + 1 = 10 (gornji primer) izpeljemo korake:

Odštejemo 1 na obeh straneh: 3x + 1 − 1 = 10 − 1, torej 3x = 9.
Delimo z 3: x = 9 / 3, torej x = 3.

Tako dobimo rešitev x = 3. To je tipična metoda za linearne enačbe prve stopnje: z uporabo osnovnih operacij (seštevanje, odštevanje, množenje, deljenje) izoliramo spremenljivko.

Temeljna pravila in lastnosti

Pri delu z algebraičnimi izrazih in enačbami je koristno poznati glavne aksiome in zakone:

Komutativnost: a + b = b + a in a × b = b × a (zaporedje seštevanja ali množenja ni pomembno).
Asociativnost: (a + b) + c = a + (b + c) in (a × b) × c = a × (b × c) (sklepanje znotraj zvezne operacije).
Distributivnost: a(b + c) = ab + ac (pomaga pri množenju vsote).

Ta pravila omogočajo poenostavljanje izrazov in reševanje enačb na standardiziran način. V osnovni algebri se pogosto vadi njihova uporaba na številnih primerih, kar vodi k razumevanju splošnih pravil, kot je prikazano z 3 + 4 = 4 + 3 {\displaystyle 3+4=4+3}. $3+4=4+3$

Polinoma in faktoriranje

Polinomi so izrazi, sestavljeni iz monomov, kot so x^2, 3x in konstante. Ena od uporab v osnovni algebri je faktoriranje, ki olajša reševanje kvadratnih enačb. Na primer:

Enačba x^2 − 5x + 6 = 0 se faktorizira kot (x − 2)(x − 3) = 0, kar daje rešitve x = 2 ali x = 3.

Učenje različnih metod (faktoriranje, kvadratna formula, popoln kvadrat) omogoča reševanje širšega nabora problemov.

Funkcije in praktična uporaba

Algebra je orodje za opis funkcionalnih odnosov — kako ena količina vpliva na drugo. Primer iz zgornjega seznama: če je dobiček izražen z izrazom 3x−10 {\displaystyle 3x-10} $3x-10$ , to pomeni, da za vsako prodano enoto (x) dobimo dodatni dobiček 3 dolarje, hkrati pa imamo fiksni odhodek 10 dolarjev.

Praktični primeri uporabe algebre:

Poslovanje: izračun dobička, prihodkov, točka rentabilnosti (break-even).
Znanost in inženiring: enačbe gibanja, električni tokovi, kemične razmerja.
Gradbeništvo: izračun količin materialov, dimenzioniranje nosilcev.
Finančne aplikacije: obrestni računi, amortizacija, napovedi rasti.

Reševanje sistemov in višje stopnje

Poleg posameznih enačb se v algebri srečamo s sistemi enačb (več enačb z več spremenljivkami). Osnovne metode vključujejo substitucijo, seštevanje/odštevanje in uporabo matrik v nadaljnjih predmetih.

Elementarna algebra se naprej povezuje z linearnimi funkcijami, kvadratnimi funkcijami in osnovami za analizo in geometrijo. Kasneje se odpre pot k abstraktni algebri (grupe, prstani, polja), ki se običajno obravnava na višjih stopnjah študija.

Nasveti za učenje algebre

Vadite preproste korake: izolirajte spremenljivko, posamično izvajajte operacije na obeh straneh enačbe.
Preverite vsako rešitev nazaj v originalno enačbo, da se izognete napakam pri predpostavkah.
Razbijte zapletene izraze z uporabo distributivnosti in kombinirajte podobne člene.
Rešujte veliko primerov in besedilnih problemov — algebra je praktično orodje, ki se najbolje uči skozi uporabo.

Pogoste napake

Nepravilno deljenje pri spremenljivkah (npr. pozabljanje, da se deljenje izvaja na obeh straneh enačbe).
Izguba ločenih členi pri razširjanju oklepajev (pozabljanje distributivnosti).
Nepravilna uporaba predznakov pri premikanju členov čez enačaj.

Osnovna algebra je temelj za mnoge nadaljnje matematične teme in praktične strokovne zvrsti. Z razumevanjem njenih osnovnih pravil in redno vajo lahko hitro pridobite samozavest pri reševanju problemov, ki vključujejo neznanke, funkcije in odnose med količinami.

Enostavni problemi algebre

Če ima enačba samo eno neznano število, jo je včasih enostavno rešiti. Neznano število se imenuje "x":

2 x + 4 = 12. {\displaystyle 2x+4=12.\,} $2x+4=12.\,$

Če želite rešiti preprosto enačbo z eno neznanko, dodajte, odštejte, pomnožite ali delite obe strani enačbe z istim številom, da bo neznanka x na eni strani enačbe. Ko je x sam po sebi na eni strani, uporabite aritmetiko, da določite znesek na drugi strani enačbe. Na primer tako, da od obeh strani zgornje enačbe odštejete 4:

2 x + 4 - 4 = 12 - 4 {\displaystyle 2x+4-4=12-4\,} $2x+4-4=12-4\,$

pridobivanje:

2 x = 8 {\displaystyle 2x=8\,} $2x=8\,$

Obe strani delimo z 2:

2 x 2 = 8 2 {\displaystyle {\frac {2x}{2}}={\frac {8}{2}}\,} ${\frac {2x}{2}}={\frac {8}{2}}\,$

pridobivanje:

x = 4. {\displaystyle x=4.\,} $x=4.\,$

To enačbo si lahko predstavljamo kot žago ali ravnotežje, pri čemer je glavni cilj, da dobimo x sam po sebi, to, kar naredimo na eni strani, moramo narediti tudi na drugi.

Opredelitve

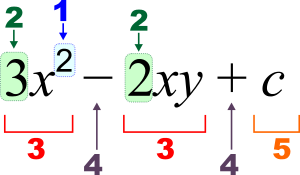
3 x 2 - 2 x y + c {\displaystyle 3x^{2}-2xy+c} $3x^{2}-2xy+c$ ima naslednje komponente:

1 : eksponent (moč), 2 : koeficient, 3 : izraz, 4 : operator, 5 : konstanta, x , y {\displaystyle x,y} : $x,y$ spremenljivke

Vprašanja in odgovori

V: Kaj je osnovna algebra?

O: Elementarna algebra je najosnovnejša oblika algebre, ki se je učijo učenci. Običajno sledi aritmetiki in vključuje uporabo spremenljivk (kot so a, x, y) za označevanje števil v enačbah.

V: Kako se uporablja osnovna algebra?

O: Elementarno algebro lahko uporabljamo za reševanje problemov z neznanimi števili, posploševanje pravil iz aritmetike, razumevanje in ustvarjanje funkcionalnih razmerij, pogosto pa se uporablja tudi pri številnih drugih predmetih, kot so znanost, poslovanje in gradbeništvo.

V: Kako osnovna algebra pomaga ljudem razumeti abstraktne ideje?

O: Elementarna algebra pomaga ljudem pri učenju splošnih idej na številnih primerih, saj dokazuje, da a+b=b+a za vse a in b. To jim omogoča boljše razumevanje abstraktnih pojmov.

V: Ali je abstraktna algebra naprednejša od osnovne algebre?

O: Da, abstraktna algebra se običajno poučuje pozno na fakulteti in je veliko naprednejša od osnovne algebre.

V: Katere vrste enačb vključuje osnovna algebra?

O: Elementarna algebra vključuje enačbe s spremenljivkami (kot so a, x, y), ki pomenijo števila, in operatorji, kot so +,- ,× in ÷ .
3x+1=10 {\displaystyle 3x+1=10}

V: Kako lahko razumevanje osnovne algebre pomaga pri drugih predmetih?

O: Razumevanje osnovne algebre lahko pomaga pri drugih predmetih, kot so znanost, poslovanje ali gradbeništvo, saj omogoča reševanje problemov o neznanih številih in ustvarjanje funkcionalnih razmerij med različnimi spremenljivkami.

Iskati