Euler-Bernoullijeva teorija nosilcev: definicija, enačbe in uporabe

Euler-Bernoullijeva teorija nosilcev: jasna definicija, ključne enačbe in praktične uporabe v gradbeništvu in strojništvu — preprosto razloženo za inženirje in študente.

Euler-Bernoullijeva teorija nosilcev (znana tudi kot inženirska teorija nosilcev ali klasična teorija nosilcev) je preprosta in široko uporabljena metoda za izračun upogibanja nosilcev pri obremenitvi. Velja za majhne deformacije nosilca in izključuje učinke strižnih deformacij, zato jo lahko obravnavamo kot poseben primer Timošenkove teorije nosilcev. Prvič je bila predstavljena okoli leta 1750 in je bila priljubljena med razvojem Eifflovega stolpa in Ferrisovega kolesa konec 19. stoletja. Pozneje se je uporabljala na številnih inženirskih področjih, vključno s strojništvom in gradbeništvom. Čeprav so bile razvite druge napredne metode, se Euler-Bernoullijeva teorija nosilcev zaradi svoje preprostosti še vedno pogosto uporablja.

Osnovne predpostavke

• Material je linearno-elastičen (Hookeov zakon) z modulom elastičnosti E, ki je stalna vzdolž preseka.
• Nosilec je tanek (razpon je bistveno večji od dimenzij preseka) in upogibanje je majhno (majhne rotacije in pomiki).
• Poprečni preseki, prečni na nevtralno os, ostanejo ravni in pravokotni na nevtralno os po upogibanju (»plane sections remain plane«).
• Učinki striženja in rotacijske vztrajnosti preseka so zanemarjeni.

Gibalna enačba

Gibalna (diferenčna) enačba za popačenje w(x) v Euler–Bernoullijevi teoriji za nosilec v ravnini je četrtega reda:
E I(x) d^4w/dx^4 = q(x),

kjer je E modul elastičnosti, I(x) drugi moment površine preseka glede na nevtralno os, q(x) pa porazdeljena obremenitev (sila na enoto dolžine). Enačba velja v linearni regiji; znake in predznake je treba uskladiti s konvencijo sile/negativne smeri pomika.

Notranje sile in napetosti

Brez razmišljanja o popačenju so osnovne količine:

• Upogibni moment M(x) in strižna sila V(x), ki ju dobimo iz diferencialnih enačb ravnotežja: dM/dx = V in dV/dx = -q(x).
• Normalna (upogibna) napetost skozi višino preseka: σ(x,y) = -M(x)·y / I, kjer je y razdalja od nevtralne osi.
• Približna strižna napetost v prerezu: τ = V·Q/(I·t), kjer je Q statični moment deleža nad točko, t pa efektivna debelina preseka pri točki.

Praktične rešitve za osnovne primere

Pri enostavno podprtih ali konzolnih nosilcih so znane zaprte oblike rešitev:

• Enostrani (konsolni) nosilec z končno silo P na koncu: maksimalni upogib w_max = P L^3 / (3 E I) in maksimalni moment M_max = P L.
• Enostavno podprt nosilec z osrednjo silo P: maksimalni upogib v sredini w_max = P L^3 / (48 E I) in maksimalni moment M_max = P L / 4.

Za porazdeljene obremenitve q(x) se rešitev enačbe pogosto izvede integracij, uporabi tabel rešitev ali numeričnih metod (npr. metoda končnih elementov).

Robni pogoji

Pri reševanju enačbe moramo navesti štiri robne pogoje (enačba 4. reda), na primer kombinacijo pomika w in rotacije θ = dw/dx ali notranjih sil (moment, strižna sila) na robovih. Pogosti tipi robnih pogojev:

• Končno podprt rob: w = 0 (ni pomika), θ svoboden (rotacija dovoljena).
• Fiksiran rob (vpet): w = 0, θ = 0.
• Prosto končni rob: M = 0, V = 0.

Omejitve in razširitve teorije

Euler-Bernoulli predpostavlja zanemarljivo strižno deformacijo, zato ni primerna, kadar:

• so kratki ali debeli nosilci (kjer so strižne deformacije pomembne); za te primere se uporablja Timošenkova teorija nosilcev;
• so velike deformacije ali nelinearne materialne lastnosti (plastičnost, velike rotacije); v tem primeru je potrebna nelinearna analiza;
• so dinamični pojavi z visokimi frekvencami in rotacijsko vztrajnostjo preseka;
• preseki so nehomogeni, kompozitni ali imajo odprta tankostenska konstrukcija, kjer se pojavi zvijanje in vohanje (warping).

Uporaba v praksi

Zaradi enostavnosti se Euler-Bernoullijeva teorija pogosto uporablja za hitro oceno upogibov in napetosti pri načrtovanju nosilnih elementov v stavbah, mostovih, krmilnih palicah, gredih, okvirih, strojnih delih ipd. Primeri vključujejo nosilce pri stavbah, tramove mostov, vrteče se elemente in osnovne komponente strojev. Ko so zahteve natančnosti višje ali so predpostavke kršene, inženirji nadaljujejo z bolj natančnimi modeli (Timoshenko, Euler-Bernoulli z upoštevanjem rotacijske vztrajnosti, metoda končnih elementov).

Kaj si zapomniti

• Euler-Bernoulli je enostaven in hiter model za upogib nosilcev pri majhnih deformacijah in tankih presekih.
• Glavna enačba: E I d^4w/dx^4 = q(x), drugi moment površine I in modul E sta ključna parametra.
• Za kratke/debele elemente ali velike strižne učinke uporabimo Timoshenko teorijo.

Zgodovina

Leonhard Euler in Daniel Bernoulli sta leta 1750 prva sestavila teorijo. Takrat so na znanost in tehniko gledali drugače kot danes. Matematičnim teorijam, kot je bila Euler-Bernoullijeva teorija žarka, niso zaupali za praktično inženirsko uporabo. Mostovi in stavbe so se do konca 19. stoletja načrtovali z enakimi metodami. Takrat sta Eifflov stolp in Ferrisovo kolo pokazala veljavnost teorije v večjem merilu.

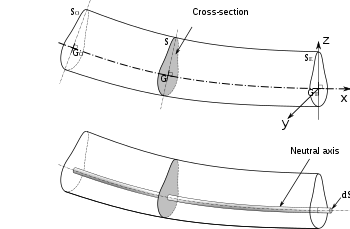
Risba prečnega prereza upognjenega nosilca z nevtralno osjo

Enačba statičnega nosilca

Euler-Bernoullijeva enačba opisuje razmerje med deformacijo nosilca in uporabljeno obremenitvijo, kot je prikazano spodaj:

d 2 d x 2 ( E I d 2 w d x 2 ) = q {\displaystyle {\frac {\mathrm {d} ^{2}}{\mathrm {d} x^{2}}}}\left(EI{\frac {\mathrm {d} ^{2}w}{\mathrm {d} x^{2}}}}}\right)=q\,}

kjer w ( x ) {\displaystyle w(x)} opisuje deformacijo nosilca v smeri z {\displaystyle z} na nekem mestu x {\displaystyle x} . q {\displaystyle q} je porazdeljena obremenitev, z drugimi besedami sila na enoto dolžine (podobno kot je tlak sila na površino); lahko je funkcija x {\displaystyle x} , w {\displaystyle w} . ali drugih spremenljivk.

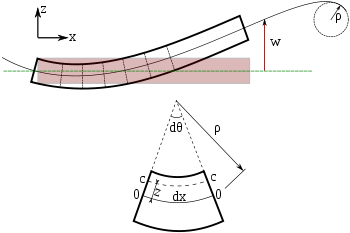
Upogibanje Euler-Bernoullijevega nosilca. Vsak prerez nosilca je pod kotom 90 stopinj glede na nevtralno os.

Vprašanja in odgovori

V: Kaj je Euler-Bernoullijeva teorija žarkov?

V: Kdaj je bila prvič predstavljena Euler-Bernoullijeva teorija nosilcev?

V: Ali je bila Euler-Bernoullijeva teorija nosilcev uporabljena pri razvoju Eifflovega stolpa in ruskega kolesa?

V: Na katerih inženirskih področjih se je uporabljala Euler-Bernoullijeva teorija nosilcev?

V: Ali se Euler-Bernoullijeva teorija nosilcev še vedno pogosto uporablja?

V: Za katere vrste deformacij nosilca velja Euler-Bernoullijeva teorija?

V: Ali Euler-Bernoullijeva teorija nosilca upošteva učinke strižnih deformacij?

Išči po črki