Hollandov izrek o shemi: definicija in vloga v genetskih algoritmih

Raziskava Hollandovega izreka o shemi: definicija, pomen v genetskih algoritmih, omejitve in povezava s Priceovo enačbo — razumljivo in poglobljeno.

Avtor: Leandro Alegsa

17-11-2025 21:38

Hollandov izrek o shemi, imenovan tudi temeljni izrek genetskih algoritmov, je neenakost, ki opisuje, kako se v populaciji genetskih algoritmov spreminjajo frekvence določenih vzorčnih rezultatov (sheem) pod vplivom selekcije, križanja in mutacije. Izrek je predlagal John Holland v sedemdesetih letih prejšnjega stoletja in je bil sprva pogosto navajan kot temeljna razlaga moči genetskih algoritmov. Kasnejše raziskave so pokazale, da je izrek koristna groba aproksimacija evolucijske dinamike, hkrati pa ima omejitve in je mogoče njegove posledice razložiti tudi s širšimi okvirji (na primer kot poseben primer Priceove enačbe z indikatorjem sheme kot makroskopsko meritvijo).

Definicija sheme in osnovne pojmi

Shema je predloga, ki določa podmnožico nizov (npr. binarnih nizov) z istimi vrednostmi na določenih pozicijah in neodločenimi vrednostmi (običajno označenimi z zvezdico *) na preostalih pozicijah. Sheme so posebna vrsta cilindričnih množic in zato tvorijo topološki prostor.

Primer sheme: za niz dolžine 6 je shema 1*0**1 množica vseh nizov, ki imajo 1 na prvi poziciji, 0 na tretji in 1 na šesti; ostale pozicije so poljubne.
Red sheme (o(H)): število določenih (ne-zvezdičnih) pozicij v shemi H. V zgornjem primeru je o(H) = 3.
Definiranje dolžine sheme (d(H)): razlika indeksa zadnje in prve določenih pozicije v shemi; v zgornjem primeru je d(H) = 6 - 1 = 5.
m(H,t): število primerkov (ali delež) posameznikov v populaciji v generaciji t, ki ustrezajo shemi H.
f(H): povprečna prilagodljivost (fitness) posameznikov, ki ustrezajo shemi H; f̄ je povprečna prilagodljivost celotne populacije.

Matematična oblika izreka

Hollandov izrek v poenostavljeni obliki napove, da se pričakovana frekvenca kratkih shem nizkega reda z nadpovprečno dobrimi lastnostmi povečuje iz generacije v generacijo. V eni običajnih zapisov za učinek proporcionalne selekcije, enopičnega križanja s verjetnostjo p_c in mutacije z verjetnostjo p_m velja spodnja neenakost (približna pričakovana vrednost):

m(H,t+1) ≥ m(H,t) · (f(H) / f̄) · [1 − p_c · (d(H)/(l−1))] · (1 − p_m)^{o(H)}

Tu je l dolžina kromosoma. Prvi člen (f(H)/f̄) odraža povečanje zaradi selekcije; drugi člen zajema verjetnost, da shema ne bo razbita z enopičnim križanjem (odvisno od definicijske dolžine); tretji člen ocenjuje verjetnost, da nobena od določenih pozicij ne bo spremenjena z mutacijo.

Intuicija in gradniki (building blocks)

Glavna intuicija izreka podpira tako imenovano hipotezo o gradnikih (building-block hypothesis): genetski algoritem naj bi iskreno združeval kratke, nizko-redne sheme z nadpovprečno dobrimi vrednostmi v večje, učinkovitejše rešitve skozi selekcijo in rekombinacijo. Ker so take sheme krajše in z majhnim številom določenih lokacij, so manj dovzetne za poškodbe zaradi križanja in mutacije in zato bolj verjetno preživijo in se združijo.

Pomembne omejitve in kritike

Aproksimacija: Izrek daje spodnjo mejo za pričakovano število primerkov sheme v naslednji generaciji, ne pa natančnega napovednika za vse situacije. Zanemarja več dejavnikov, kot so stohastičnost, kompleksne oblike križanja in odvisnosti med različnimi geni (epistaza).
Pogojne predpostavke: Ključne predpostavke vključujejo proporcionalno selekcijo in specifične modele operacij (npr. enopično križanje). Pri drugih oblikah selekcije ali križanja je oblika izraza drugačna ali manj uporabna.
Epistaza in kompleksne interakcije: Ko so vplivi genov medsebojno močno povezani (epistaza), lahko kratke sheme ne predstavljajo zanesljivih gradnikov za uspeh, saj kombinacija več genov hkrati vpliva na fitness.
Stohastičnost in naključne fluktuacije: V majhnih populacijah lahko naključne spremembe (genetski drift) preglasijo pričakovane deterministične učinke, ki jih napoveduje izrek.
Relacija do Priceove enačbe: Kasnejše teoretične analize so pokazale, da je Hollandov izrek poseben primer širših formulacij evolucijske dinamike, na primer Priceove enačbe, kjer je funkcija indikatorja sheme uporabljena kot makroskopska mera za skupino posameznikov.

Vloga izreka v praksi

Hollandov izrek je pomemben predvsem kot konceptualno orodje: pojasnjuje, zakaj lahko enostavni genetski operatorji (selektivno množenje, križanje, mutacija) vodijo v gradnjo dobrih rešitev preko iterativnega združevanja obetavnih delov rešitev. V praksi pa pri snovanju in analizi genetskih algoritmov raziskovalci upoštevajo tudi njegove omejitve in pogosto uporabljajo eksperimentalne študije, naprednejše modele (npr. modelne populacije, bolj zapletene operatorje) ali alternativne teoretične pristope za natančnejše napovedi obnašanja algoritma.

Kratek primer

Predstavljajmo si populacijo 8-binarnimi nizi dolžine 5. Shema H = 1*1** ima o(H)=2 (določeni sta poziciji 1 in 3) in d(H)=3−1=2. Če ima povprečna prilagodljivost članov sheme f(H) večjo od povprečja populacije f̄, bo po izreku pričakovano število teh člena v naslednji generaciji večje, ob predpostavki, da križanje in mutacija sheme ne razbijeta prepogosto.

Izrek torej ne obljublja univerzalne rešitve, vendar daje teoretično podlago za razumevanje, kako selekcija in recombinacija lahko vodita do eksponentne rasti obetavnih kombinacij v populaciji genetskih algoritmov.

Opis

Upoštevajte binarne nize dolžine 6. Shema 1*10*1 opisuje množico vseh nizov dolžine 6 z 1 na položajih 1, 3 in 6 ter 0 na položaju 4. Znak * je nadomestni simbol, kar pomeni, da imata lahko položaja 2 in 5 vrednost 1 ali 0. Vrstni red sheme o ( H ) {\displaystyle o(H)} $o(H)$ je opredeljen kot število fiksnih položajev v predlogi, medtem ko je definicijska dolžina δ ( H ) {\displaystyle \delta (H)} $\delta (H)$ razdalja med prvim in zadnjim določenim položajem. Vrstni red 1*10*1 je 4, njegova definicijska dolžina pa 5. Primernost sheme je povprečna primernost vseh nizov, ki ustrezajo shemi. Primernost niza je merilo vrednosti kodirane rešitve problema, kot jo izračuna za problem specifična ocenjevalna funkcija. Z uporabo uveljavljenih metod in genetskih operatorjev genetskih algoritmov izrek o shemi pravi, da se kratke sheme nizkega reda z nadpovprečnim fitnesom v zaporednih generacijah eksponentno povečujejo. Izražen kot enačba:

E ( m ( H , t + 1 ) ) ≥ m ( H , t ) f ( H ) a t [ 1 - p ] . {\displaystyle \operatorname {E} (m(H,t+1))\geq {m(H,t)f(H) \over a_{t}}[1-p]. } $\operatorname {E} (m(H,t+1))\geq {m(H,t)f(H) \over a_{t}}[1-p].$

Pri tem je m ( H , t ) {\displaystyle m(H,t)} $m(H,t)$ število nizov, ki pripadajo shemi H {\displaystyle H} $H$ v generaciji t {\displaystyle t} $t$ , f ( H ) {\displaystyle f(H)} $f(H)$ je opazovana povprečna primernost sheme H {\displaystyle H} $H$ in a t {\displaystyle a_{t}} $a_{t}$ je opazovana povprečna primernost v generaciji t {\displaystyle t} $t$ . Verjetnost prekinitve p {\displaystyle p} $p$ je verjetnost, da bosta križanje ali mutacija uničila shemo H {\displaystyle H} $H$ . Lahko jo izrazimo kot:

p = δ ( H ) l - 1 p c + o ( H ) p m {\displaystyle p={\delta (H) \over l-1}p_{c}+o(H)p_{m}} $p={\delta (H) \over l-1}p_{c}+o(H)p_{m}$

kjer je o ( H ) {\displaystyle o(H)} $o(H)$ vrstni red sheme, l {\displaystyle l} $l$ dolžina kode, p m {\displaystyle p_{m}} $p_{m}$ verjetnost mutacije in p c {\displaystyle p_{c}} $p_{c}$ verjetnost križanja. Zato je verjetnost, da bo shema s krajšo definicijsko dolžino δ ( H ) {\displaystyle \delta (H)} $\delta (H)$ prekinjena, manjša.
Pogosto napačno razumljena točka je, zakaj je izrek o shemi neenakost in ne enakost. Odgovor je pravzaprav preprost: izrek zanemarja majhno, a ne ničelno verjetnost, da bo niz, ki pripada shemi H {\displaystyle H} $H$ , nastal "iz nič" z mutacijo enega samega niza (ali rekombinacijo dveh nizov), ki v prejšnji generaciji ni pripadal H {\displaystyle H} . $H$

Omejitev

Izrek o shemah velja ob predpostavki genetskega algoritma, ki vzdržuje neskončno veliko populacijo, vendar se ne prenese vedno na (končno) prakso: zaradi napake pri vzorčenju v začetni populaciji lahko genetski algoritmi konvergirajo k shemam, ki nimajo selektivne prednosti. To se zgodi zlasti pri multimodalni optimizaciji, kjer ima lahko funkcija več vrhov: populacija lahko začne dajati prednost enemu od vrhov, druge pa zanemarja.

Razlog, da teorem o shemi ne more pojasniti moči genetskih algoritmov, je v tem, da velja za vse primere problemov in ne more razlikovati med problemi, pri katerih genetski algoritmi delujejo slabo, in problemi, pri katerih genetski algoritmi delujejo dobro.

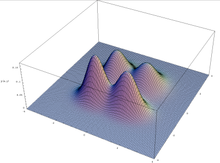
Graf multimodalne funkcije v dveh spremenljivkah.

Vprašanja in odgovori

V: Kaj je Hollandov teorem o shemi?

O: Hollandov teorem o shemi je teorem o genetskih algoritmih, ki pravi, da je večja verjetnost, da bodo prevladali posamezniki, katerih fitnes je višji od povprečja.

V: Kdo in kdaj je predlagal Hollandov teorem o shemi?

O: John Holland je Hollandov teorem sheme predlagal v sedemdesetih letih prejšnjega stoletja.

V: Kaj je shema v kontekstu genetskih algoritmov?

O: V kontekstu genetskih algoritmov je shema predloga, ki določa podmnožico nizov s podobnostmi na določenih pozicijah nizov.

V: Kakšna je razlaga Hollandovega teorema o shemi, ki je bil uporabljen kot temelj za razlage moči genetskih algoritmov?

O: Razlaga Hollandovega teorema o shemi, ki je bil uporabljen kot temelj za razlage moči genetskih algoritmov, je, da imajo posamezniki, katerih fitnes je višji od povprečja, večjo verjetnost, da bodo prevladali.

V: Kaj je pokazala kritika Hollandovega teorema o shemi?

O: Kritika Hollandovega teorema o shemi je pokazala, da je poseben primer Priceove enačbe s funkcijo indikatorja sheme kot makroskopsko meritvijo.

V: Kaj je poseben primer valjastih množic?

O: Sheme so poseben primer valjastih množic.

V: Kakšno vrsto prostora tvorijo sheme?

O: Sheme tvorijo topološki prostor.

Iskati