Normalna sila
Normalna sila je sila, s katero tla (ali katera koli druga površina) potiskajo nazaj navzgor. Če ne bi bilo normalne sile, bi se počasi vpijali v tla.
Normalna sila na predmet je vedno pravokotna (pod pravim kotom) na površino, na kateri je predmet.
Na ravni površini je normalna sila predmeta m g {\displaystyle mg} 
(teža predmeta, to je njegova masa, pomnožena s silo teže).
Na nagnjeni ravnini se normalna sila zmanjša za kot in normalna sila je m g c o s θ {\displaystyle mgcos\theta } 
.
Upoštevajte, da je na ravni površini θ {\displaystyle \theta }
enak 0, zato je c o s θ {\displaystyle cos\theta }
enak 1. Zato sta enačbi enaki.
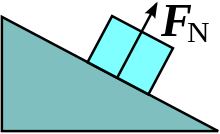
FN predstavlja normalno silo
Vprašanja in odgovori
V: Kaj je normalna sila?
O: Normalna sila je sila, s katero tla (ali katera koli druga površina) potiskajo nazaj navzgor.
V: Kaj bi se zgodilo, če ne bi bilo normalne sile?
O: Če ne bi bilo normalne sile, bi se počasi pogreznili v tla.
V: Kako je normalna sila na predmet povezana z njegovo težo?
O: Na ravni površini je normalna sila na predmet enaka njegovi teži (masa predmeta, pomnožena s silo teže).
V: Kako naklonjena ravnina vpliva na normalno silo?
O: Na nagnjeni ravnini se normalna sila zmanjša za kot in jo lahko izračunamo z uporabo m g c o s θ.
V: Kaj pomeni θ v tej enačbi?
O: V tej enačbi θ predstavlja kot nagiba.
V: Kdaj je cosθ enak 1?
O: cosθ je 1, ko je θ (kot) enak 0, kar se zgodi na ravni površini.
V: Kako se ti dve enačbi primerjata med seboj? O: Enačbi sta enaki, kadar sta na ravni površini.
