Elipsa
Elipsa je oblika, ki je videti kot oval ali sploščen krog.
V geometriji je elipsa ravninska krivulja, ki nastane s presečiščem stožca z ravnino tako, da nastane zaprta krivulja.
Krogi so posebni primeri elips, ki jih dobimo, če je rezalna ravnina pravokotna na os stožca. Elipsa je tudi prostor vseh točk ravnine, katerih razdalje do dveh fiksnih točk so enake konstanti.
Krog ima eno središče, imenovano žarišče, elipsa pa ima dve žarišči.
Elipsa so preprosto vse točke na grafu, katerih vsota razdalj od dveh točk je enaka. Elipso lahko na primer naredimo tako, da v karton zapičimo dva žebljička in okoli njiju naredimo krog iz vrvice, nato v zanko vstavimo svinčnik in vlečemo v vse smeri, kolikor je mogoče, ne da bi vrvico pretrgali. Obeležitve planetov so elipse, pri čemer je Sonce v enem oglišču, v drugem pa ni ničesar.
Enačba elipse je : ( x - h ) 2 a 2 + ( y - k ) 2 b 2 = 1 {\displaystyle {\frac {(x-h)^{2}}{a^{2}}}+{\frac {(y-k)^{2}}{b^{2}}}}=1}}
kjer je središče elipse (h,k). 2A je dolžina od obeh koncev daljše in bolj tanke stranice. 2b je dolžina dveh koncev krajše stranice. A²-B²=C², pri čemer je c dolžina med ogliščem in središčem.
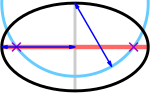
Oglišča (vijolični križci) so na presečiščih glavne osi (rdeča) in kroga (cian) s polmerom, ki je enak polveliki osi (modra), s središčem na koncu male osi (siva).
Elipso dobimo kot presečišče stožca z ravnino.
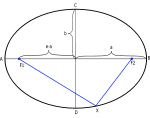
Elipsa in njene lastnosti.
Vprašanja in odgovori
V: Kaj je elipsa?
O: Elipsa je oblika, ki je videti kot oval ali sploščen krog. V geometriji je to ravninska krivulja, ki nastane kot posledica preseka stožca z ravnino tako, da nastane zaprta krivulja.
V: Kako ustvarimo elipso?
O: Elipso lahko naredimo tako, da v karton zapičimo dva žebljička, okoli teh dveh žebljičkov napeljemo vrvico, v zanko vstavimo svinčnik in vlečemo v vse smeri, kolikor je mogoče, ne da bi vrvico pretrgali.
V: Kaj so krogi posebni primeri?
O: Krogi so posebni primeri elips, ki nastanejo, če je rezalna ploskev pravokotna na os stožca.
V: Koliko oglišč ima elipsa?
O: Elipsa ima dve oglišči.
V: Katera enačba opisuje elipso?
O: Enačba za elipso je (x - h)²/a² + (y - k)²/b² = 1, kjer h in k predstavljata središče elipse, 2a predstavlja dolžino med koncema daljše in krajše stranice, 2b pa dolžino med koncema krajše stranice. C predstavlja dolžino med ogliščem in središčem, tako da je A²-B²=C².
V: Kje vidimo primere eliptičnih orbit?
O: Elipsaste orbite lahko vidimo pri planetih, katerih sonce je v enem od oglišč.
