Linearna regresija
Linearna regresija je način za pojasnitev razmerja med odvisno spremenljivko in eno ali več pojasnjevalnimi spremenljivkami z uporabo premice. Je poseben primer regresijske analize.
Linearna regresija je bila prva vrsta regresijske analize, ki je bila natančno preučena. To pa zato, ker je modele, ki so linearno odvisni od svojih neznanih parametrov, lažje prilagoditi kot modele, ki so nelinearno povezani s svojimi parametri. Poleg tega je lažje določiti statistične lastnosti dobljenih ocenjevalcev.
Linearna regresija ima veliko praktičnih uporab. Večina aplikacij spada v eno od naslednjih dveh širših kategorij:
- Linearno regresijo lahko uporabimo za prileganje napovednega modela na niz opazovanih vrednosti (podatkov). To je koristno, če je cilj napovedovanje, napovedovanje ali zmanjšanje. Če je po oblikovanju takšnega modela podana dodatna vrednost X brez spremljajoče vrednosti y, se lahko vgrajeni model uporabi za napovedovanje vrednosti y.
- Ob spremenljivki y in več spremenljivkah X1, ..., Xp, ki so lahko povezane z y, se lahko linearna regresijska analiza uporabi za količinsko opredelitev moči povezave med y in Xj, za oceno, katera Xj sploh ni povezana z y, in za določitev, katere podmnožice Xj vsebujejo odvečne informacije o y.
Pri linearnih regresijskih modelih se poskuša doseči, da je navpična razdalja med premico in podatkovnimi točkami (npr. ostanki) čim manjša. To imenujemo "prilagajanje premice podatkom". Linearni regresijski modeli pogosto poskušajo čim bolj zmanjšati vsoto kvadratov ostankov (najmanjši kvadrati), vendar obstajajo tudi drugi načini prilagajanja. Ti vključujejo minimiziranje "pomanjkanja ujemanja" v neki drugi normi (kot pri regresiji z najmanjšimi absolutnimi odstopanji) ali minimiziranje kaznovane različice funkcije izgube najmanjših kvadratov, kot pri regresiji z grebeni. Pristop najmanjših kvadratov se lahko uporabi tudi za prilagajanje modelov, ki niso linearni. Kot je opisano zgoraj, sta izraza "najmanjši kvadrati" in "linearni model" tesno povezana, vendar nista sopomenki.
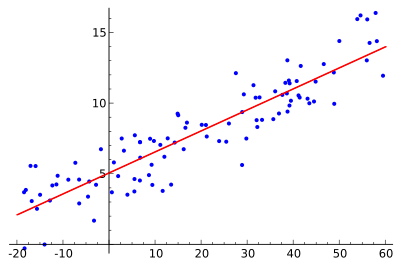
Ideja je najti rdečo krivuljo, modre točke pa so dejanski vzorci. Pri linearni regresiji lahko vse točke povežemo z eno samo ravno črto. V tem primeru je uporabljena preprosta linearna regresija, pri kateri je kvadrat razdalje med rdečo črto in vsako vzorčno točko minimiziran.
Uporaba
Ekonomija
Linearna regresija je glavno analitično orodje v ekonomiji. Uporablja se na primer za ocenjevanje potrošnje, investicij v osnovna sredstva, investicij v zaloge, nakupov izvoza države, izdatkov za uvoz, povpraševanja po likvidnih sredstvih, povpraševanja po delu in ponudbe dela.
Vprašanja in odgovori
V: Kaj je linearna regresija?
O: Linearna regresija je način matematičnega preučevanja, kako se nekaj spremeni, ko se spremenijo druge stvari. Uporablja odvisno spremenljivko in eno ali več pojasnjevalnih spremenljivk, da bi ustvarila ravno črto, znano kot "regresijska črta".
V: Katere so prednosti linearne regresije?
O: Modele, ki so linearno odvisni od svojih neznanih parametrov, je lažje prilagoditi kot modele, ki so nelinearno povezani s svojimi parametri. Poleg tega je lažje določiti statistične lastnosti dobljenih ocenjevalcev.
V: Katere so praktične uporabe linearne regresije?
O: Linearno regresijo lahko uporabimo za prileganje napovednega modela opazovanim vrednostim (podatkom), da bi naredili napovedi, napovedi ali redukcije. Uporablja se lahko tudi za količinsko opredelitev moči razmerij med spremenljivkami in za prepoznavanje podskupin podatkov, ki vsebujejo odvečne informacije o drugi spremenljivki.
V: Kako poskušajo linearni regresijski modeli zmanjšati napake?
O: Linearni regresijski modeli si prizadevajo, da bi bila navpična razdalja med premico in podatkovnimi točkami (ostanki) čim manjša. To se doseže z minimiziranjem vsote kvadratov ostankov (najmanjši kvadratki), pomanjkanja ujemanja v neki drugi normi (najmanjša absolutna odstopanja) ali z minimiziranjem penalizirane različice izgubne funkcije najmanjših kvadratov (regresija grebenov).
V: Ali je mogoče, da modeli linearne regresije ne temeljijo na metodi najmanjših kvadratov?
O: Da, možno je, da modeli linearne regresije ne temeljijo na metodi najmanjših kvadratov, ampak se namesto tega uporabljajo metode, kot sta minimizacija pomanjkanja ujemanja v neki drugi normi (najmanjša absolutna odstopanja) ali minimizacija kaznovane različice izgubne funkcije najmanjših kvadratov (regresija grebena).
V: Ali sta "linearni model" in "najmanjši kvadrat" sinonima?
O: Ne, nista sinonima. Čeprav sta tesno povezana, se "linearni model" nanaša predvsem na uporabo ravne črte, medtem ko se "najmanjši kvadrati" nanašajo predvsem na poskus zmanjšanja napak z zagotavljanjem minimalne navpične razdalje med črto in podatkovnimi točkami.
