Pregled matrične mehanike: Heisenberg, matrike in načelo negotovosti
Pregled matrične mehanike: od Heisenberga in matrik do Heisenbergovega načela negotovosti — zgodovina, ključni koncepti in uporabe v kvantni fiziki.
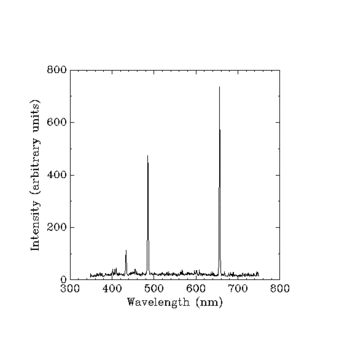
Matrična mehanika je prvi način, ki so ga fiziki našli za matematično izražanje kvantne fizike. Werner Heisenberg je to obliko izražanja fizikalnih zakonov sprva razvil kot enačbo, s katero je lahko napovedal intenzivnost fotonov v različnih pasovih vodikovega spektra.

Heisenbergov učitelj in kolega Max Born je videl, da je njegova enačba v bistvu načrt za ustvarjanje in množenje matrik. Matrična oblika kvantne fizike se še vedno uporablja, saj je za nekatere namene koristna in priročna. Drugi matematični načini, zlasti enačba Erwina Schrödingerja z uporabo valovne funkcije, so matematično enakovredni, vendar jih je lažje uporabljati za druge namene.
Eden od prvih uspehov te teorije je bil objavljen kmalu zatem in se zdaj imenuje Heisenbergovo načelo negotovosti.
Kaj pomeni »matrična« v tem kontekstu
V matrični mehaniki so fizikalne količine (opazovalne velikosti) predstavljene z matrikami oziroma operaterji, ki delujejo na vektorjih stanj v Hilbertovem prostoru. Metrike vsebujejo elemente, ki pogosto predstavljajo prehodne amplitude med energijskimi stanji — na primer verjetnost in fazo prehoda elektronov med dvema nivojema. Merljivi rezultati so lastne vrednosti teh operatorjev, verjetnosti pa izhajajo iz komponent lastnih vektorjev (stanj) in njihovih amplitud.
Ključne lastnosti in posledice
- Nekomutativnost: Matrike (operatorji) v splošnem ne komutirajo, torej AB ≠ BA. Ta lastnost je osnovna pri kvantnih pojavih in vodi do omejitev, kaj lahko hkrati merimo natančno.
- Komutator: Za dve opazovalni veličini A in B se uporabi komutator [A,B] = AB − BA. Za položaj x in gibalno količino p velja kanonična zveza [x,p] = iħ, kar je matematična osnova za negotovostni odnos med njima.
- Časovni razvoj: V Heisenbergovi sliki se operatorji spreminjajo v času, medtem ko so stanja fiksna; v Schrödingerjevi sliki (valovna funkcija) se pa spreminjajo stanja. Obe sliki sta matematično ekvivalentni in dajeta enake napovedi.
Heisenbergovo načelo negotovosti – razlaga
Heisenbergovo načelo negotovosti pravi, da za določene pare opazovalnih količin (kot sta položaj in gibalna količina) ne moremo hkrati in poljubno natančno določiti obeh vrednosti. Ta trditev izhaja matematično iz nekomutativnosti pripadajočih operatorjev in se izrazi z nižnjo mejo za produkt standardnih odklonov ΔA in ΔB. V splošni obliki velja odnos podobnega tipa: ΔA · ΔB ≥ (1/2) |⟨[A,B]⟩|, pri čemer je ⟨[A,B]⟩ pričakovana vrednost komutatorja v danem stanju. Za položaj in gibalno količino to vodi na tipično obliko Δx · Δp ≥ ħ/2.
Kratka zgodovinska pripomba
Heisenberg je leta 1925 zabeležil kvantne rezultate kot tabele tranzicijskih amplitud. Max Born je hitro prepoznal, da gre za matrike in da je potrebno uporabiti algebraične zakonitosti množenja matrik. V sodelovanju s Pascualom Jordanom in drugimi so kmalu razvili popolno teorijo matrične mehanike, ki je skupaj s Schrödingerjevo valovno mehaniko tvorila temelj kvantne teorije.
Zakaj je matrična mehanika še vedno uporabna danes
- Za sisteme z diskretnimi energijskimi nivoji ali majhnimi Hilbertovimi prostori (npr. spin-1/2, kvantne vrzeli, modelne kvantne logične enote) je matrična oblika pogosto najpriročnejša.
- Uporablja se v teoriji gostih snovi, kvantnem računanju, opisih kvantne dinamike (enote, časovna evoulcija U(t)=exp(−iHt/ħ)) in pri numeričnih izračunih z gostimi ali redkimi matrikami.
- Koncepti, kot so Paulijeve matrike, gostota-matrika (density matrix) in komutatorji, so osrednji elementi sodobne kvantne teorije in eksperimentalne analize.
Kako povezati matrično in valovno (Schrödingerjevo) mehaniko
Obe formulaciji dajeta iste fizikalne napovedi. Razlika je predvsem v predstavitvi: Schrödingerjeva formulacija uporablja valovne funkcije in diferencialne enačbe, matrična pa linearno-algebraične metode. V praksi izberemo tisto obliko, ki poenostavi računanje za obravnavani problem (npr. diferencialne enačbe pri kontinuiranih potencialih ali matrike pri diskretnih sistemih).
Na kratko: matrična mehanika je elegantna matematična struktura za opis kvantnih pojavov, njeni temelji pa (nekomutativnost in spektralna narava operatorjev) nudijo neposredno razlago za bistvene lastnosti kvantnega sveta, kot je Heisenbergovo načelo negotovosti.
Vprašanja in odgovori
V: Kaj je matrična mehanika?
O: Matrična mehanika je oblika izražanja fizikalnih zakonov, ki jo je razvil Werner Heisenberg in ki uporablja matrike za napovedovanje jakosti fotonov v različnih pasovih vodikovega spektra.
V: Kdo je razvil matrično mehaniko?
O: Werner Heisenberg je sprva razvil matrično mehaniko kot enačbo za napovedovanje jakosti fotonov v različnih pasovih vodikovega spektra.
V: Kako so jo odkrili?
O: Max Born je opazil, da je Heisenbergova enačba v bistvu načrt za ustvarjanje in množenje matrik, kar je privedlo do odkritja matrične mehanike.
V: Ali se še vedno uporablja?
O: Da, matrična mehanika se še vedno uporablja, saj je za nekatere namene uporabna in priročna.
V: Ali obstajajo še drugi matematični načini za izražanje kvantne fizike?
O: Da, enačba Erwina Schrödingerja z uporabo valovne funkcije je matematično enakovredna, vendar jo je lažje uporabiti za druge namene.
V: Kateri je bil zgodnji uspeh, povezan s to teorijo?
O: Eden od zgodnjih uspehov, povezanih s to teorijo, je bilo Heisenbergovo načelo negotovosti.
V: Kdo je napovedal ta uspeh kmalu po njegovem razvoju?
O: Ta uspeh je kmalu po njegovem razvoju razglasil Werner Heisenberg.
Iskati