Heisenbergovo načelo negotovosti

Zmeda z učinkom opazovalca

V preteklosti so načelo negotovosti zamenjali z nekoliko podobnim učinkom v fiziki, imenovanim učinek opazovalca. Ta pravi, da meritev nekaterih sistemov ni mogoče opraviti, ne da bi vplivali na sisteme. Heisenberg je tak učinek opazovalca na kvantni ravni ponudil kot fizikalno "razlago" kvantne negotovosti.

Vendar je zdaj jasno, da je načelo negotovosti lastnost vseh valovno podobnih sistemov. V kvantni mehaniki se pojavi preprosto zaradi valovne narave vseh kvantnih objektov. Tako načelo negotovosti dejansko navaja temeljno lastnost kvantnih sistemov in ni izjava o uspešnosti opazovanja sedanje tehnologije. "Merjenje" ne pomeni le procesa, v katerem sodeluje fizik - opazovalec, temveč vsako interakcijo med klasičnimi in kvantnimi objekti ne glede na opazovalca.

Zamisel o nedoločenosti

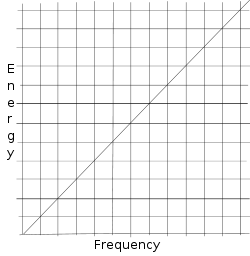
Načelo negotovosti izhaja iz matrične mehanike Wernerja Heisenberga. Že Max Planck je vedel, da je energija enote svetlobe sorazmerna s frekvenco te enote svetlobe ( E ∝ ν {\displaystyle E\propto \nu } ) in da lahko njeno količino energije izrazimo z znanimi izrazi, kot je džul, z uporabo konstante sorazmernosti. Konstanto, ki jo je dal svetu, zdaj imenujemo Planckova konstanta in jo označujemo s črko h. Kadar se za izražanje kvantne mehanike uporabljajo matrike, je treba pogosto pomnožiti dve matriki, da dobimo tretjo matriko, ki daje odgovor, ki ga fizik poskuša najti. Toda če pomnožimo matriko, kot je P (za gibalno moč), z matriko, kot je X (za lego), dobimo drugačno matriko z odgovorom, kot če pomnožimo X s P. Rezultat pomnožitve P z X in X s P ter njune primerjave vedno vključuje Planckovo konstanto kot faktor. Število, ki ga uporabimo za zapis Planckove konstante, je vedno odvisno od uporabljenega merilnega sistema. (Pri določenem merilnem sistemu je njena številčna vrednost ena.) Tudi naklon črte na diagramu na desni, ki prikazuje razmerje med frekvenco in energijo, je odvisen od izbranega merilnega sistema.

Naslednja diagrama prikazujeta, kaj se zgodi, če poskušamo izmeriti tako lokacijo kot gibanje.

Praktični rezultat tega matematičnega odkritja je, da ko fizik pojasni položaj, postane gibalna moč manj jasna, in ko fizik pojasni gibalno moč, postane položaj manj jasen. Heisenberg je dejal, da so stvari "nedoločljive", drugi pa so radi rekli, da so "negotove". Toda matematika kaže, da so stvari v svetu nedoločljive ali "nejasne", in ne, da je negotovo le to, da smo ljudje negotovi glede tega, kaj se dogaja.

Široka odprtina, ostro ostrenje


Z zmanjšanjem vrzeli se poveča gotovost, kje je foton v sredini, vendar je njegova smer od tam do detekcijskega zaslona na desni strani ustrezno bolj negotova.


Ozka luknja, razpršeno ostrenje


Če sredinsko vrzel obesimo z vzmetmi, lahko izmerimo zagon, vendar se vrzel nepredvidljivo premakne, zato se informacija o lokaciji fotona v sredini izgubi.


Vzmetno nameščena luknja meri zagon

Prevedba nedoločenosti v matematično obliko

Tukaj bomo prikazali prvo enačbo, ki je dala osnovno idejo, kasneje prikazano v Heisenbergovem načelu negotovosti.

Heisenbergov prelomni članek iz leta 1925 ne uporablja in niti ne omenja matrik. Heisenbergov velik uspeh je bila "shema, s katero je bilo mogoče načeloma nedvoumno določiti ustrezne fizikalne lastnosti (prehodne frekvence in amplitude)" vodikovega sevanja.

Ko je Heisenberg napisal svoj prelomni članek, ga je dal enemu od svojih učiteljev, da ga popravi, in odšel na počitnice. Maxa Borna so zmedle enačbe in nekomutacijske enačbe, ki so se celo Heisenbergu zdele problematične. Po nekaj dneh je Born ugotovil, da so te enačbe navodila za zapisovanje matrik. Matrike so bile nove in nenavadne celo za takratne matematike, vendar je bilo že jasno znano, kako z njimi matematizirati. Skupaj z nekaj drugimi je vse razvil v obliki matrik, preden se je Heisenberg vrnil s svojega dopusta, in v nekaj mesecih je nova kvantna mehanika v obliki matrik dala podlago za še en članek.

Max Born je opazil, da matriki, ki predstavljata pq in qp, nista enaki. Heisenberg je isto videl že pri svojem prvotnem načinu zapisovanja in morda je uganil, kar je bilo Bornu skoraj takoj jasno - da bo razlika med matrikami odgovorov za pq in qp vedno vključevala dva faktorja, ki sta izhajala iz Heisenbergove prvotne matematike: Planckova konstanta h in i, ki je kvadratni koren iz negativne ena. Tako se je v Heisenbergovih izvirnih enačbah skrivala sama ideja, ki jo je Heisenberg raje imenoval "načelo nedoločenosti" (običajno znano kot načelo negotovosti).

Heisenberg je preučeval spremembe, ki se zgodijo v atomu, ko elektron spremeni svoj energijski nivo in se tako približa središču atoma ali oddalji od središča, in še posebej primere, ko elektron v dveh korakih pade v nižje energijsko stanje. Max Born je pojasnil, kako je prevzel Heisenbergov nenavadni "recept" za iskanje produkta C neke spremembe v atomu z energijske ravni n na energijsko raven n-b, ki je vključeval vsoto množenja ene spremembe nečesa, kar se imenuje A (kar je lahko na primer frekvenca nekega fotona), ki jo povzroči sprememba energije elektrona v atomu med energijskima stanjema n in n-a), z naslednjo spremembo nečesa, kar se imenuje B (kar je lahko na primer amplituda spremembe), ki jo povzroči druga sprememba energijskega stanja z n-a na n-b):

C ( n , n - b ) = ∑ a A ( n , n - a ) B ( n - a , n - b ) {\displaystyle C(n,n-b)=\sum _{a}^{}\,A(n,n-a)B(n-a,n-b)}

in odkril nekaj revolucionarnega:

Heisenberg je s preučevanjem ... primerov...[Heisenberg] ugotovil to pravilo.... To je bilo poleti leta 1925. Heisenberg ... je vzel dopust ... in mi predal svoj članek v objavo....

Heisenbergovo pravilo množenja me ni pustilo pri miru in po tednu dni intenzivnega razmišljanja in preizkušanja sem se nenadoma spomnil algebrske teorije....Take kvadratne matrike so matematikom precej znane in jih v povezavi z določenim pravilom množenja imenujemo matrike. To pravilo sem uporabil za Heisenbergov kvantni pogoj in ugotovil, da se za diagonalne elemente ujema. Ni bilo težko uganiti, kaj morajo biti preostali elementi, namreč nič; in takoj se je pred mano pojavila nenavadna formula

Q P - P Q = i h 2 π {\displaystyle {QP-PQ={\frac {ih}{2\pi }}}}
[Simbol Q je matrika za premik, P je matrika za gibanje, i pomeni kvadratni koren negativne ena, h pa Planckovo konstanto.]

Kasneje je Heisenberg svoje odkritje prenesel v drugo matematično obliko:

Δ x Δ p ≥ ℏ 2 {\displaystyle \Delta x\,\Delta p\geq {\frac {\hbar }{2}}}

(Posebni simbol ℏ {\displaystyle {\hbar }} se imenuje "h-bar" ali "reducirana Planksova konstanta" in je enak h 2 π {\displaystyle {\frac {h}{2\pi }}} .)

Matematika je način opisovanja stvari, ki se dogajajo v resničnem svetu. Morda si predstavljate, da bi bilo enostavno dobiti natančen položaj nečesa ter hkrati njegovo maso, pot in hitrost. Vendar pa morate v resnici narediti dve stvari, da dobite odgovor. Če merite položaj in gibanje krogle, ki se je zataknila v skalo velike gore, je to preprosta zadeva. Ni videti, da bi se gora kam premikala, prav tako ne krogla. Njen položaj je torej znan, njena hitrost pa je enaka 0, zato je tudi njen zagon enak 0. Če pa je krogla nekje med orožjem in tarčo, bo v vsakem trenutku težko ugotoviti njen položaj. Najboljše, kar lahko storimo, je, da jo posnamemo s fotoaparatom z zelo hitrim zaklopom. Toda z enim samim pritiskom na zaklop bi dobili le eno stvar, položaj krogle v času t. Da bi dobili gibalno silo, bi lahko krogli na pot postavili kocko parafina in izmerili, kako se kocka parafina premakne, ko ustavi kroglo. Če pa bi poznali maso krogle, bi lahko posneli zaporedje dveh slik in izračunali hitrost, tako da bi poznali razliko med dvema položajema krogle in časom med njenima pojavitvama. Kakor koli že, izmeriti moramo maso in položaj ter čas med pojavljanjem. Na koncu opravimo vsaj dve meritvi, da dobimo x in p. V tem primeru moramo izbrati, katero meritev bomo opravili najprej in katero drugič. Zdi se, da je vseeno, v kakšnem vrstnem redu bomo opravili meritve. Če bi izmerili maso krogle in nato dvakrat izmerili njene položaje ali dvakrat izmerili položaje krogle in nato ponovno izbrali kroglo ter izmerili njeno maso, ne bi bilo nobene razlike, kajne? Navsezadnje s kroglo nismo naredili ničesar, ko smo jo tehtali ali fotografirali.

Na zelo majhnem merilu, ko merimo nekaj, kot je elektron, pa vsaka meritev nekaj naredi z njim. Če najprej izmerimo lego, pri tem spremenimo njegov momemtum. Če najprej izmerimo elektronov momentum, potem v procesu spremenimo njegov položaj. Upali bi, da bi izmerili enega in nato drugega, preden bi se kar koli spremenilo, vendar že naše merjenje samo po sebi povzroči spremembo in najboljše, kar lahko upamo, je, da bomo zmanjšali energijo, ki jo z merjenjem prispevamo elektronu, na najmanjšo možno mero. Ta najmanjša količina energije ima kot enega od faktorjev Planckovo konstanto.

Negotovost presega matrično matematiko

Heisenbergovo načelo negotovosti je bilo najdeno v prvih enačbah "nove" kvantne fizike, teorija pa je bila podana z uporabo matematike matrik. Vendar je načelo negotovosti dejstvo o naravi in se kaže v drugih načinih govorjenja o kvantni fiziki, na primer v enačbah, ki jih je sestavil Erwin Schrödinger.

Nedoločenost v naravi, ne negotovost ljudi

Heisenbergovo odkritje se obravnava na dva zelo različna načina: Nekateri menijo, da so stvari, ki se dogajajo v naravi, "determinirane", to pomeni, da se stvari dogajajo po določenem pravilu, in če bi lahko vedeli vse, kar moramo vedeti, bi lahko vedno rekli, kaj se bo zgodilo naslednjič. Drugi ljudje menijo, da stvari, ki se dogajajo v naravi, vodi le verjetnost in da lahko vemo le, kako se bodo stvari obnašale v povprečju - vendar to vemo zelo natančno.

Fizik John Stewart Bell je odkril način, kako dokazati, da prvi način ne more biti pravilen. Njegovo delo se imenuje Bellov teorem ali Bellova neenakost.

Priljubljena kultura

Izraz "kvantni skok" ali "kvantni skok" je bil vzet kot izraz za veliko in transformativno spremembo in se pogosto uporablja v hiperboličnih izrazih politikov in v prodajnih kampanjah v množičnih medijih. V kvantni mehaniki se uporablja za opis prehoda elektrona iz ene orbite okoli jedra atoma v katero koli drugo orbito, višjo ali nižjo.

Včasih se beseda "quantum" uporablja v imenih komercialnih izdelkov in podjetij. Podjetje Briggs and Stratton na primer proizvaja številne vrste majhnih bencinskih motorjev za kosilnice, rotacijske kultivatorje in druge majhne stroje. Eden od njihovih modelov se imenuje "Quantum".

Ker načelo negotovosti pravi, da določenih meritev na atomski ravni ni mogoče opraviti, ne da bi to vplivalo na druge meritve, nekateri posamezniki to idejo uporabljajo za opis primerov v človeškem svetu, ko opazovalčeva dejavnost spremeni opazovano stvar. Antropolog se lahko odpravi v kakšen oddaljen kraj, da bi se naučil, kako ljudje tam živijo, vendar lahko dejstvo, da jih opazuje nenavadna oseba iz zunanjega sveta, spremeni način, kako ti ljudje ravnajo.

Stvari, ki jih ljudje počnejo med opazovanjem in ki spremenijo opazovano, so primeri učinka opazovalca. Nekatere stvari, ki jih počnejo ljudje, povzročajo spremembe na zelo majhni ravni atomov in so primeri negotovosti ali nedoločenosti, kot jih je prvi opisal Heisenberg. Načelo negotovosti kaže, da vedno obstaja meja, kako majhni so lahko določeni pari meritev, na primer položaj in hitrost ali trajektorija in zagon. Učinek opazovalca pravi, da ima lahko včasih to, kar ljudje naredijo pri opazovanju stvari, npr. spoznavanje kolonije mravelj, ko jo prekopavajo z vrtnim orodjem, velike učinke, ki spremenijo to, kar so skušali spoznati.