Verjetnost: osnovna definicija, pravila in primeri v praksi
Verjetnost je veja uporabne matematike, ki preučuje naključne pojave — dogodke, ki se lahko zgodijo ali pa ne. Z učenjem verjetnosti napovemo, kako verjetno je, da se bo določen dogodek zgodil, in te informacije uporabimo v znanosti, igrah na srečo, zavarovalništvu, statistiki in vsakdanjih odločitvah.
Osnovna definicija
Verjetnost dogodka A običajno označimo s P(A). Velja: 0 ≤ P(A) ≤ 1. Če je P(A) = 0, je dogodek nemogoč; če je P(A) = 1, je dogodek gotov. Verjetnost lahko predstavljamo kot ulomek, decimalno število ali odstotek (npr. 1/2 = 0,5 = 50%).
Enostavni primeri: kovanec in kocka
Pri metanju običajnega kovanca sta običajno samo dva izida: "glava" in "rep". Če je kovanec pošten (simetričen), je verjetnost vsake strani 1/2 — torej pri velikem številu metov bo približno polovica metov pokazala glavo in polovica rep.
Pri metanju kocke (če velja, da je množina možnih izidov {1,2,3,4,5,6} in so izidi enako verjetni), je verjetnost vsakega posameznega števila 1/6. Verjetnost, da pade katero koli število od 1 do 6, je 1.
Kako računamo verjetnosti — osnovna pravila
- Aksiomi verjetnosti: (1) P(A) ≥ 0; (2) P(Ω) = 1 (Ω je celotna množica možnih izidov); (3) če sta A in B disjunktna (ne moreta nastopiti hkrati), potem P(A ∪ B) = P(A) + P(B).
- Komplement: P(A') = 1 − P(A), kjer A' pomeni, da se A ne zgodi.
- Vsota za poljubna dogodka: P(A ∪ B) = P(A) + P(B) − P(A ∩ B). Če sta disjunktna, se drugi člen izniči.
- Multiplikacijsko pravilo (neodvisna dogodka): Če sta A in B neodvisna, potem P(A ∩ B) = P(A) × P(B).
- Splošno multiplikacijsko pravilo (pogojna verjetnost): P(A ∩ B) = P(A) × P(B | A), kjer je P(B | A) verjetnost B, če vemo, da se je A zgodil.
Primeri množenja verjetnosti (neodvisni dogodki)
Ena zanimivih lastnosti naključja je, da, kadar želimo verjetnost, da se zgodita dva neodvisna dogodka zaporedoma, pomnožimo njuni verjetnosti. Na primer, verjetnost, da pri dvakratnem metanju kocke najprej pade 3, potem 5, je 1/6 × 1/6 = 1/36 ≈ 0,027777... Če nas zanima, da se v treh metih zaporedoma pojavita 3, nato 5 in nato 2, je verjetnost 1/6 × 1/6 × 1/6 = 1/216 ≈ 0,0046296.
Če vrstni red ni pomemben (npr. želimo dobiti en 3 in en 5 v dveh metih, v kateremkoli vrstnem redu), upoštevamo vse možne urejene izide: verjetnost takega dogodka je 2 × (1/36) = 1/18, ker sta mogoča izida (3,5) in (5,3).
Pogojna verjetnost in odvisnost
Pogojna verjetnost P(B | A) pomeni verjetnost dogodka B, če vemo, da se je A že zgodil. Če dogodka nista neodvisna, potem P(A ∩ B) ≠ P(A)P(B) in uporabimo formulo P(A ∩ B) = P(A)P(B | A). Primer odvisnosti: če iz vreče brez vračanja vzamemo prvo kroglico rdeče barve, se verjetnost naslednje rdeče spremeni.
Kratka razlaga različnih interpretacij verjetnosti
- Klasčna (teoretična): če so vsi izidi enako verjetni, P(A) = (število ugodnih izidov) / (število vseh izidov).
- Pogostnostna (empirična): P(A) približamo z deležem, kolikokrat se je A zgodil v velikem številu ponovitev.
- Bayesovska (subjektivna): verjetnost predstavlja stopnjo prepričanja glede dogodka, ki se lahko posodablja z novimi podatki.
Praktični nasveti in primeri
- Pri računih najprej določite, ali so izidi enako verjetni. Če so, uporabite klasično metodo (štetje izidov).
- Pri več zaporednih dogodkih preverite, ali so dogodki neodvisni (npr. met kovanca brez spreminjanja kovanca). Če so neodvisni, množite verjetnosti; če ne, uporabite pogojne verjetnosti.
- Pri problemih z veliko kombinacijami (npr. vsota šestih kock) uporabite račun verjetnosti s kombinatoriko ali računalniško simulacijo; v praksi se pogosto uporabi programsko štetje vseh možnih izidov ali Monte Carlo simulacije.
Verjetnost je torej orodje, s katerim kvantificiramo negotovost. Z nekaj osnovnimi pravili in prakso lahko rešujemo zelo različne naloge — od preprostih metov kovanca do zapletenih statističnih modelov.
Več o računskih postopkih in uporabi verjetnosti v matematiki lahko najdete tudi pri matematiko.
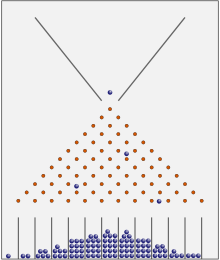
V stroju za fižol ali Galtonovi škatli se večina kroglic konča blizu sredine. Na dolgi rok bodo imele normalno porazdelitev.
Ideje o verjetnosti
Ljudje, kot so Jacob Bernoulli, Pierre-Simon Laplace ali Christiaan Huygens, so uporabljali besedo verjetnost, kot je opisano zgoraj. Drugi ljudje so razmišljali o frekvencah; njihov pojem verjetnosti se običajno imenuje frekvenčna verjetnost.
Sorodne strani
- Seznam matematičnih tem
- Teorija verjetnosti
Vprašanja in odgovori
V: Kaj je verjetnost?
O: Verjetnost je del uporabne matematike, ki se ukvarja s preučevanjem stvari, ki se lahko zgodijo ali pa se ne zgodijo.
V: Kako je mogoče izraziti verjetnost?
O: Verjetnost lahko izrazimo s številom med nič (nemogoče) in ena (gotovo).
V: Kakšen je primer uporabe verjetnosti?
O: Primer uporabe verjetnosti je dokaz, da če vržemo kovanec v zrak in ga pustimo, da pristane, bo polovico časa pristal z eno stranjo navzgor, polovico časa pa z drugo stranjo navzgor.
V: Kako izračunamo verjetnost, da bomo vrgli dve kocki in dobili določeno kombinacijo?
O: Če želite izračunati verjetnost, da bosta dve kocki padli in dobili določeno kombinacijo, morate pomnožiti obe verjetnosti skupaj. Če bi na primer želeli izvedeti, ali bo padla trojka in nato še petica, bi bila verjetnost 1/6 x 1/6 = 1/36.
V: Kaj pomeni "rep", ko govorimo o kovancih?
O: Ko govorimo o kovancih, se "rep" nanaša na stran brez obraza ali slike.
V: Kako verjetno je, da boš vrgel šest kock in dobil število, večje od deset? O: Verjetnost, da boš vrgel šest kock in dobil število, večje od deset, je mogoče ugotoviti s pomočjo matematike in znanosti, vendar ni očitna.
V: Kaj se zgodi, če pomnožimo dve verjetnosti?
O: Ko pomnožite dve verjetnosti skupaj, izračunate možnost, da se obe stvari zgodita hkrati.
