Planckova konstanta

Ozadje

Simboli, uporabljeni v tem članku.
Simbol Pomen E Energija h Planckova konstanta k Boltzmannova konstanta c hitrost svetlobe λ valovna dolžina sevanja ν frekvenca sevanja T absolutna temperatura

Med letoma 1670 in 1900 so znanstveniki razpravljali o naravi svetlobe. Nekateri znanstveniki so menili, da je svetloba sestavljena iz več milijonov drobnih delcev. Drugi znanstveniki so menili, da je svetloba valovanje.

Svetloba: valovi ali delci?

Christiaan Huygens je leta 1678 napisal knjigo Traité de la lumiere ("Razprava o svetlobi"). Menil je, da je svetloba sestavljena iz valov. Trdil je, da svetloba ne more biti sestavljena iz delcev, saj se svetloba dveh žarkov ne odbija drug od drugega. Leta 1672 je Isaac Newton napisal knjigo Optike. Menil je, da je svetloba sestavljena iz rdečih, rumenih in modrih delcev, ki jih je imenoval telesca. Newton je to razložil s poskusom z dvema prizmama. Prva prizma je svetlobo razbila na različne barve. Druga prizma je te barve združila nazaj v belo svetlobo.

V 18. stoletju je bila Newtonova teorija deležna največ pozornosti. Leta 1803 je Thomas Young opisal poskus z dvojno režo. Pri tem poskusu svetloba, ki gre skozi dve ozki reži, interferira sama s seboj. To povzroči vzorec, ki pokaže, da je svetloba sestavljena iz valov. Do konca devetnajstega stoletja je bila valovna teorija svetlobe deležna največ pozornosti. V šestdesetih letih 19. stoletja je James Clerk Maxwell razvil enačbe, ki so opisovale elektromagnetno sevanje kot valovanje.

Teorija elektromagnetnega sevanja obravnava svetlobo, radijske valove, mikrovalove in številne druge vrste valovanja kot isto stvar, le da imajo različne valovne dolžine. Valovna dolžina svetlobe, ki jo vidimo z očmi, je približno med 400 in 600 nm. Valovna dolžina radijskih valov je od 10 m do 1500 m, valovna dolžina mikrovalov pa je približno 2 cm. V vakuumu vsi elektromagnetni valovi potujejo s svetlobno hitrostjo. Frekvenca elektromagnetnega valovanja je podana z:

ν = c λ {\displaystyle \nu ={\frac {c}{\lambda }}}.

Simboli so opredeljeni tukaj.

Črni radiatorji za telo

Vse tople stvari oddajajo toplotno sevanje, ki je elektromagnetno sevanje. Za večino stvari na Zemlji je to sevanje v infrardečem območju, vendar nekaj zelo vročega (1000 °C ali več) oddaja vidno sevanje, to je svetlobo. Konec 19. stoletja so številni znanstveniki preučevali valovne dolžine elektromagnetnega sevanja črnih teles pri različnih temperaturah.

Pravo Rayleigh-Jeans

Lord Rayleigh je leta 1900 prvič objavil osnove Rayleigh-Jeansovega zakona. Teorija je temeljila na kinetični teoriji plinov. Sir James Jeans je leta 1905 objavil popolnejšo teorijo. Zakon povezuje količino in valovno dolžino elektromagnetne energije, ki jo oddaja sevalec črnega telesa pri različnih temperaturah. Enačba, ki to opisuje, je:

B λ ( T ) = 2 c k T λ 4 {\displaystyle B_{\lambda }(T)={\frac {2ckT}{\lambda ^{4}}}}.

Pri sevanju dolgih valovnih dolžin so se rezultati, predvideni s to enačbo, dobro ujemali s praktičnimi rezultati, pridobljenimi v laboratoriju. Pri kratkih valovnih dolžinah (ultravijolična svetloba) pa je bila razlika med teorijo in prakso tako velika, da si je prislužila vzdevek "ultravijolična katastrofa".

Planckov zakon

leta 1895 je Wien objavil rezultate svojih raziskav o sevanju črnega telesa. Njegova formula je bila:

B λ ( T ) = 2 h c 2 λ 5 e - h c λ k T {\displaystyle B_{\lambda }(T)={\frac {2hc^{2}}{\lambda ^{5}}}e^{-{\frac {hc}{\lambda kT}}}} .

Ta formula se je dobro obnesla pri elektromagnetnem sevanju kratkih valovnih dolžin, ni pa se dobro obnesla pri dolgih valovnih dolžinah.

Leta 1900 je Max Planck objavil rezultate svojih študij. Poskušal je razviti izraz za sevanje črnega telesa, izražen z valovno dolžino, tako da je predpostavil, da je sevanje sestavljeno iz majhnih kvantov, in nato preveril, kaj se zgodi, če so kvanti neskončno majhni. (To je standardni matematični pristop). Izraz je bil naslednji:

B λ ( T ) = 2 h c 2 λ 5 1 e h c λ k T - 1 {\displaystyle B_{\lambda }(T)={\frac {2hc^{2}}{\lambda ^{5}}}~{\frac {1}{e^{\frac {hc}{\lambda kT}}-1}}}.

Če je valovna dolžina svetlobe zelo velika, lahko dokažemo, da sta Raleigh-Jeansovo in Planckovo razmerje skoraj enaka.

Izračunal je h in k ter ugotovil, da

h = 6,55×10⁻²⁷ erg-sek.

k = 1,34×10 ⁻¹⁶erg-deg ^-1.

Vrednosti so blizu sodobno sprejetim vrednostim 6,62606×10⁻³⁴ oziroma 1,38065×10. ⁻¹⁶Planckov zakon se dobro ujema z eksperimentalnimi podatki, vendar je bil njegov pomen v celoti spoznan šele nekaj let pozneje.

Kvantna teorija svetlobe

Izkazalo se je, da se elektroni zaradi fotoelektričnega učinka izločijo, če svetloba doseže mejno frekvenco. Pod to vrednostjo se iz kovine ne morejo oddati nobeni elektroni. Leta 1905 je Albert Einstein objavil članek, v katerem je razložil ta učinek. Einstein je predlagal, da svetlobni snop ni valovanje, ki se širi po prostoru, temveč skupek diskretnih valovnih paketov (fotonov), od katerih ima vsak energijo. Einstein je trdil, da je učinek posledica trka fotona z elektronom. S tem je dokazal delčno naravo svetlobe.

Einstein je tudi ugotovil, da elektromagnetno sevanje z veliko valovno dolžino nima učinka. Einstein je menil, da je to zato, ker "delci" niso imeli dovolj energije, da bi motili elektrone.

Plank je predlagal, da je energija vsakega fotona povezana s frekvenco fotona s Planckovo konstanto. To lahko matematično zapišemo kot:

E = h ν = h c λ {\displaystyle E=h\nu ={\frac {hc}{\lambda }}}.

Plank je leta 1918 prejel Nobelovo nagrado za zasluge, ki jih je z odkritjem energijskih kvantov prispeval k napredku fizike. Einstein je leta 1921 prejel Nobelovo nagrado za povezavo Planckove konstante s fotoelektričnim učinkom.

Ilustracija iz Newtonovega izvirnega pisma Kraljevi družbi (1. januar 1671 [julijanski koledar]). S predstavlja sončno svetlobo. Svetloba med ravninama BC in DE je obarvana. Te barve se rekombinirajo in tvorijo sončno svetlobo na ravnini GH


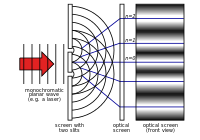
Youngov poskus z dvojno režo


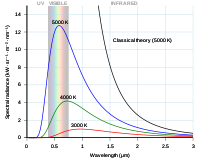
Rayleigh-Jeansova krivulja in Planckova krivulja, izrisani glede na valovno dolžino fotona.


Konferenca Solway 1911. Planck, Einstein in Jeans stojijo. Planck je drugi z leve. Einstein je drugi z desne. Jeans je peti z desne. Wien sedi, tretji z desne.

Aplikacija

Planckova konstanta je pomembna za številne aplikacije. Nekaj jih je naštetih v nadaljevanju.

Bohrov model atoma

Leta 1913 je Niels Bohr objavil Bohrov model zgradbe atoma. Bohr je dejal, da ima lahko kotni moment elektronov, ki krožijo okoli jedra, le določene vrednosti. Te vrednosti so podane z enačbo

L = n h 2 π {\displaystyle L=n{\frac {h}{2\pi }}}

kjer je

L = kotni moment, povezan s stopnjo.

n = pozitivno celo število.

h = Planckova konstanta.

Z Bohrovim modelom atoma lahko izračunamo energijo elektronov na vsakem nivoju. Elektroni običajno zapolnijo najnižje oštevilčena stanja v atomu. Če atom prejme energijo, na primer iz električnega toka, se elektroni vzbudijo v višje stanje. Elektroni bodo nato padli nazaj v nižje stanje in izgubili svojo dodatno energijo z oddajo fotona. Ker imajo energijski nivoji določene vrednosti, imajo tudi fotoni določene energijske nivoje. Tako oddano svetlobo lahko s pomočjo prizme razdelimo na različne barve. Vsak element ima svoj vzorec. Vzorec za neon je prikazan v nadaljevanju.

Heisenbergovo načelo negotovosti

Leta 1927 je Werner Heisenberg objavil načelo negotovosti. To načelo pravi, da ni mogoče izvesti meritve, ne da bi pri tem motili merjeno stvar. Določa tudi mejo najmanjše motnje, ki jo povzroči meritev.

V makroskopskem svetu so te motnje zelo majhne. Če na primer merimo temperaturo erlenmajerice s tekočino, bo termometer pri segrevanju absorbiral majhno količino energije. To povzroči majhno napako v končnem odčitku, vendar je ta napaka majhna in ni pomembna.

V kvantni mehaniki je drugače. Nekatere meritve se opravijo z opazovanjem vzorca razpršenih fotonov. Tak primer je Comptonovo sipanje. Če se merita položaj in gibalna moč delca, načelo negotovosti pravi, da obstaja kompromis med natančnostjo, s katero se meri gibalna moč, in natančnostjo, s katero se meri položaj. Enačba, ki opisuje ta kompromis, je:

Δ x Δ p ≳ h {\displaystyle \Delta x\,\Delta p\gtrsim h\qquad \qquad \qquad }

kjer je

Δp = negotovost gibalne sile.

Δx = negotovost položaja.

h = Planckova konstanta.

Barva svetlečih diod

V električnem vezju, prikazanem na desni strani, je padec napetosti na svetleči diodi (LED) odvisen od materiala LED. Pri silicijevih diodah je padec napetosti 0,6 V, pri diodah LED pa med 1,8 V in 2,7 V. Ta podatek uporabniku omogoča izračun Planckove konstante.

Energija, ki jo potrebuje en elektron za preskok potencialne pregrade v materialu LED, je podana z

E = Q e V L {\displaystyle E=Q_{e}V_{L}\,}

kjer je

Q_e je naboj enega elektrona.

V_L je padec napetosti na LED diodi.

Ko elektron ponovno razpade, odda en foton svetlobe. Energija fotona je podana z isto enačbo, ki se uporablja pri fotoelektričnem učinku. Če ti enačbi združimo, sta valovna dolžina svetlobe in napetost povezani z

λ = h c V L Q e {\displaystyle \lambda ={\frac {hc}{V_{L}Q_{e}}},}

Iz tega razmerja lahko izračunate spodnjo tabelo.

Barva	Valovna dolžina (nm)	Napetost
rdeča luč	650	1.89
zelena luč	550	2.25
modra svetloba	470	2.62

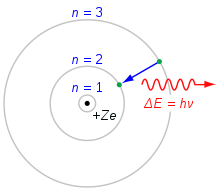
Bohrov model atoma. Elektron, ki pade iz lupine n=3 v lupino n=2, izgubi energijo. Ta energija se prenese kot en sam foton.


Vidni spekter neona. Vsaka črta predstavlja drug par energijskih nivojev.


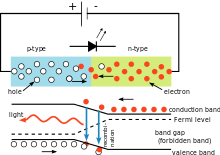
Enostavno vezje LED, ki ponazarja uporabo Planckove konstante. Barva oddane svetlobe je odvisna od padca napetosti na diodi. Valovno dolžino svetlobe lahko izračunamo z uporabo Planckove konstante.

Vrednost Planckove konstante in redefinicija kilograma

Od odkritja h so se meritve h precej izboljšale. Planck je prvič navedel vrednost h 6,55×10 ⁻²⁷erg-sek. Ta vrednost je za 5 % nižja od sedanje vrednosti.

Od 3. marca 2014 je najboljša meritev h v enotah SI 6,62606957×10⁻³⁴ J-s. Enakovredna vrednost v enotah cgs je 6,62606957×10 ⁻²⁷erg-sec. Relativna negotovost h je 4,4×10 ⁻⁸.

Zmanjšana Planckova konstanta (ħ) je vrednost, ki se včasih uporablja v kvantni mehaniki. Definirana je z

ℏ = h 2 π {displaystyle \hbar ={\frac {h}{2\pi }}}.

V kvantni mehaniki se včasih namesto SI uporabljajo Planckove enote. V tem sistemu ima reducirana Planckova konstanta vrednost 1, zato je vrednost Planckove konstante 2π.

Planckovo konstanto je zdaj mogoče izmeriti z zelo visoko natančnostjo. Zaradi tega je BIPM začel razmišljati o novi opredelitvi kilograma. Mednarodni prototip kilograma se ne uporablja več za opredelitev kilograma. Namesto tega BIPM opredeljuje Planckovo konstanto kot natančno vrednost. Znanstveniki uporabljajo to vrednost ter opredelitvi metra in sekunde za določitev kilograma.

 

Vrednost teoretične Planckove konstante

Planckovo konstanto lahko izpeljemo tudi matematično:

 

h = μ 0 π 12 c 3 [ q 0 [ 0,9163 a 0 ] 2 ] 2 f 1 r 5 ⋅ s = 6,63 × 10 - 34 J ⋅ s {\displaystyle h={\frac {\mu _{0}\pi }{12c^{3}}}{[{q_{0}}{[0,9163a_{0}]}^{2}]^{2}}{f_{1r}}^{5}\cdot {s}=6,63\krat 10^{-34}J\cdot s}

Tu je μ 0 {\displaystyle \mu _{0}} prepustnost prostega prostora, c {\displaystyle c} svetlobna hitrost, q 0 {\displaystyle q_{0}} električni naboj elektrona, a 0 {\displaystyle a_{0}} Bohrov polmer in f 1 r {\displaystyle f_{1r}} frekvenca obrata elektrona v atomu vodika ( f 1 r = 3.29 × 10 15 r e v / s ) {\displaystyle (f_{1r}=3,29\krat 10^{15}rev/s)} . Ko te vrednosti konstant nadomestimo s teoretično Planckovo konstanto, je teoretična vrednost Planckove konstante popolnoma enaka eksperimentalni vrednosti.

Sorodne strani

• Dvojnost valov in delcev