Načelo nedoločenosti

Diagrami

6. Ta animacija prikazuje eno od pomembnih posledic negotovosti vesolja: kvantno tuneliranje elektronov. Pozorno si ga oglejte. Vsakič, ko se majhen delček prebije skozi pregrado.


5. Če sredinsko vrzel obesimo na vzmetne tehtnice, lahko izmerimo zagon, vendar se pri tem vrzel nepredvidljivo premakne, tako da se informacije o lokaciji vsakega fotona v sredini izgubijo.


4. Vzmet, ki je pritrjena na oviro z majhno luknjo, povzroči, da se delec iztisne skozi luknjo, kar potisne oviro, raztegne vzmeti in tako izmeri gibalno silo. Ker pa se ovira, nameščena na vzmeti, premika, smo manj prepričani, kje je bil delec, ko je šel skozi luknjo, in tudi difrakcija bo vplivala na njegov položaj na detekcijskem zaslonu.


3. Z zožitvijo luknje se poveča gotovost, kje je foton v sredini, vendar je njegova smer od tam do detekcijskega zaslona na desni strani ustrezno bolj negotova. Ostrenje postane zamegljeno. Če luknjo razširimo, se vsi fotoni znajdejo na sredini zaslona za zaznavanje, vendar imamo potem manjšo predstavo o tem, kje so bili, ko so šli skozi osrednjo pregrado.


1. Fotoni, elektroni in drugi subatomski delci se bodo izstrelili skozi veliko luknjo, vendar ne vemo natančno, kje so bili na sredini poti.


2. Z zoževanjem luknje se poti delcev ob robovih luknje ukrivijo (difrakcija), zato je nastali žarek večji in mehkejši.

Kako so se ljudje naučili o negotovosti?

Kmalu po tem, ko je Werner Heisenberg ustvaril novo kvantno fiziko, je iz njegove matematike izšlo nekaj nepričakovanega, izraz:

Δ x Δ p ≳ h 4 π {\displaystyle \Delta x\,\Delta p\gtrsim {\frac {h}{4\pi }}\qquad \qquad \qquad }

Razpon napake v položaju (x), pomnožen z napako v gibanju (p), je približno enak ali večji od Planckove konstante, deljene s 4π.

Ti simboli v matematični obliki izražajo to, kar ste že videli na zgornjih slikah. Simboli na jasen način povedo, da ne morete biti popolnoma prepričani, kje nekaj je in kam gre. Če vam je v vsakem trenutku bolj jasno, kje je, potem imate manjšo predstavo o tem, kje je in kako hitro gre. Če vam je jasneje, kam gre in kako hitro, potem imate manjšo predstavo o tem, kje je zdaj.

Znanstveniki so že ugotovili, zakaj nekatere snovi oddajajo značilne barve svetlobe, ko se segrejejo ali kako drugače vzburijo. Heisenberg je poskušal pojasniti, zakaj imajo te barve značilno svetlost. Ne bi bilo dovolj, če bi on in drugi znanstveniki samo rekli: "No, tako pač je." Prepričani so bili, da mora obstajati dober razlog za te razlike in za dejstvo, da so razmerja med jakostmi svetlih črt vedno enaka za vsak vzorec elementa.

Ko se je lotil odkrivanja razlage intenzivnosti barvnih črt, značilnih za vsak element, ni vedel, da bo naletel na skrito skrivnost narave. Študij kvantne mehanike je že pokazal, zakaj ima vodik štiri svetle črte v delu spektra, ki ga lahko vidimo ljudje. Verjetno se je zdelo, da se bo treba naučiti le, kako izračunati njihovo svetlost. Vodik se je zdel očitna izbira za začetek, saj ima le en elektron in le štiri črte v vidnem delu spektra. Zagotovo mora obstajati dober razlog, da niso enako svetle. Razlaga za svetlost različno obarvanih črt neona in drugih elementov je lahko počakala.

 

Heisenberg se je kvantne fizike lotil tako, da je prilagodil klasične enačbe za elektriko, ki so na začetku zelo zapletene, zato je bilo matematiki v njegovem članku iz leta 1925 zelo težko slediti.

Poskušal je najti pravi način za izračun intenzivnosti svetlih črt v spektru vodikove svetilke. Poiskati je moral sorodno količino, imenovano "amplituda", in pomnožiti amplitudo z amplitudo (z drugimi besedami, amplitudo je moral kvadratizirati), da je dobil želeno jakost. Ugotoviti je moral, kako izraziti amplitudo na način, ki bi upošteval dejstvo, da vodikove sijalke ne sevajo pri vseh frekvencah in ne sevajo v neprekinjenem frekvenčnem območju v delu spektra, ki ga ljudje lahko vidijo. Heisenberg je našel izjemen nov način izračuna amplitude.

Nenavadna enačba, ki jo je Heisenberg odkril in uporabil za množenje ene kvantne količine (npr. položaja) z drugo (npr. gibanja), je bila objavljena v tako imenovanem "Heisenbergovem 'čarobnem' članku iz julija 1925".

C ( n , n - b ) = ∑ a A ( n , n - a ) B ( n - a , n - b ) {\displaystyle C(n,n-b)=\sum _{a}^{}\,A(n,n-a)B(n-a,n-b)}

Zgornja matematika je videti zelo težka, vendar je matematika, ki vodi do nje, še veliko težja in jo je zelo težko razumeti. Tukaj je navedena samo zato, da pokažemo, kako je izgledala. Heisenbergov članek je zgodovinski mejnik. Številni fiziki, ki so prebrali njegov članek, so dejali, da se ne morejo ne strinjati z njegovimi sklepi, vendar ne morejo slediti njegovi razlagi, kako je prišel do teh sklepov. Začetne enačbe, ki jih je Heisenberg uporabil, so vključevale Fourierjeve vrste in številne faktorje. K zgornji enačbi se bomo še vrnili, saj je nekakšen recept za zapisovanje in množenje matrik.

Nove enačbe so morale biti tako nenavadne in nenavadne, ker je Heisenberg opisoval nenavaden svet, v katerem se nekatere stvari, kot so orbite elektronov, ne povečujejo ali zmanjšujejo počasi. Nove vrste sprememb vključujejo skoke in velike vrzeli med skoki. Elektroni lahko skačejo le med določenimi orbitami, energija, pridobljena ali izgubljena pri spremembi med orbitami, pa nastane, ko se absorbira foton ustrezne energije ali proizvede nov foton ustrezne energije. Če elektroni v vodikovih atomih najpogosteje skačejo navzdol (padajo) med dvema določenima orbitama, se bo na tej energijski ravni oddalo več fotonov, zato bo svetloba, proizvedena na tej ravni, najintenzivnejša.

Težko je bilo prilagoditi enačbe za zvezne spektre (ki jih vidimo, ko spustimo sončno svetlobo skozi prizmo) spektrom, ki imajo le nekaj najvišjih frekvenc, med katerimi ni ničesar. Skoraj vse, kar smo se do tedaj naučili o svetlobi in energiji, je bilo narejeno za velike predmete, kot so goreče sveče ali sonce, in ti veliki predmeti ustvarjajo zvezne spektre. Čeprav je bilo s temi stvarmi običajne velikosti enostavno izvajati poskuse, je še vedno trajalo veliko časa, da smo ugotovili zakonitosti (fizike), ki veljajo zanje. Zdaj so se fiziki ukvarjali s stvarmi, ki so bile premajhne, da bi jih videli, s stvarmi, ki niso proizvajale neprekinjenih spektrov, in so poskušali najti način, da bi iz tega, kar so že vedeli, dobili vsaj namige, ki bi jim pomagali najti zakone teh majhnih in luknjičastih virov svetlobe.

Prvotne enačbe so se nanašale na vibrirajoče telo, ki bi proizvajalo valovanje, podobno kot trstenica v orglah proizvaja zvočno valovanje z značilno frekvenco. Tako je prišlo do gibanja naprej in nazaj (kot pri vibriranju trstike) in do oddajanja valovanja, ki ga je bilo mogoče narisati v obliki sinusnega vala. Veliko tega, kar je bilo prej ugotovljeno o fiziki na atomski ravni, je bilo povezano z elektroni, ki so se gibali okoli jeder. Ko se masa giblje po orbiti, ko se vrti okoli nekega središča, ima tako imenovani "kotni moment". Kotni moment je način, na katerega se nekaj, kot je vrtiljak, še naprej vrti, ko ga ljudje nehajo potiskati. Matematika, ki se uporablja za izračun faze in kotnega momenta, je zapletena. Poleg tega Heisenberg v svojem članku iz leta 1925 ni prikazal vseh svojih izračunov, zato imajo lahko tudi dobri matematiki težave pri dopolnjevanju tistega, česar ni povedal.

Čeprav so številni fiziki trdili, da ne morejo razumeti različnih matematičnih korakov v Heisenbergovem prelomnem članku, je v nedavnem članku, ki poskuša razložiti, kako je Heisenberg prišel do svojega rezultata, uporabljenih dvajset strani, polnih matematike. Tudi tega članka ni lahko razumeti. Matematika se je začela z zelo težkimi stvarmi, na koncu pa je dala nekaj razmeroma preprostega, kar je prikazano na vrhu tega članka. Doseči preprostejši rezultat ni bilo enostavno, zato ne bomo poskušali prikazati procesa prehoda od zastarele slike vesolja do nove kvantne fizike. Potrebujemo le dovolj podrobnosti, da pokažemo, da se je skoraj takoj, ko je Heisenberg naredil svoj preboj, pokazal del delovanja vesolja, ki ga nihče prej ni videl.

Heisenberg je moral biti zelo navdušen, a tudi zelo utrujen, ko mu je pozno ponoči končno uspel preboj in si je začel dokazovati, da bo to delovalo. Skoraj takoj je opazil nekaj nenavadnega, nekaj, kar se mu je zdelo kot nadležna majhna težava, ki bi jo lahko nekako odpravil. Vendar se je izkazalo, da je bila ta majhna nadloga veliko odkritje.

Heisenberg si je prizadeval za množenje amplitud z amplitudami, zdaj pa je imel dober način za izražanje amplitude z novo enačbo. Seveda je razmišljal o množenju in o tem, kako bi množil stvari, ki so bile podane v obliki zapletenih enačb.

Heisenberg se je zavedal, da bo poleg kvadratne amplitude sčasoma želel pomnožiti tudi položaj z impulzom ali energijo s časom, in zdelo se je, da bi bilo pomembno, če bi v teh novih primerih spremenil vrstni red. Heisenberg je menil, da ne bi smelo biti pomembno, ali pomnožimo položaj z gibanjem ali pa pomnožimo gibanje s položajem. Če bi šlo za preprosta števila, ne bi bilo težav. Toda oboje so bile zapletene enačbe in izkazalo se je, da se način, kako dobiti številke za vstavljanje v enačbi, razlikuje glede na to, na kateri način ste začeli. V naravi je bilo treba izmeriti položaj in nato gibalno moč ali pa je bilo treba izmeriti gibalno moč in nato položaj, v matematiki pa je prevladovala ista splošna situacija. (Če želite izvedeti podrobnosti, si oglejte članek Heisenberg's entryway to matrix mechanics na angleški Wikipediji!) Drobne, a nadležne razlike med rezultati bodo ostale, ne glede na to, kako zelo si je Heisenberg želel, da bi izginile.

Heisenberg se takrat ni mogel znebiti tega majhnega problema, vendar je bil izčrpan, zato je svoje delo predal neposrednemu nadrejenemu Maxu Bornu in odšel na dopust.

Max Born je bil izjemen matematik, ki je kmalu ugotovil, da je enačba, ki mu jo je dal Heisenberg, nekakšen recept za zapis matrike. Dr. Born je bil v tistem času eden redkih ljudi, ki jih je zanimala ta nenavadna vrsta matematike, za katero je večina ljudi menila, da ni dobra za kaj dosti. Vedel je, da je matrike mogoče množiti, tako da je bilo mogoče vse izračune za upoštevanje enega fizikalnega problema opraviti z množenjem ene matrike z drugo. Že samo to, da bi lahko zapleten postopek spravil v standardno in sprejemljivo obliko, bi mu olajšalo delo. Morda bi ga lažje sprejeli tudi drugi ljudje.

Born je bil tako dober matematik, da je skoraj takoj ugotovil, da bo zamenjava vrstnega reda množenja obeh matrik dala drugačen rezultat, ki se bo razlikoval le za malenkost. Ta količina bi bila h/2πi. V vsakdanjem življenju bi bila ta razlika tako majhna, da je sploh ne bi opazili.

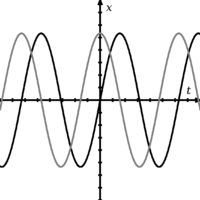
Dva valova, ki nista v medsebojni fazi


Neonski spekter


Celoten vidni spekter sonca. Ni vrzeli. Ta diagram prikazuje intenzivnost pri različnih frekvencah.


Ko se nekatere molekule vzburijo, oddajajo značilno barvo.


Spekter vodika

O formalni teoriji negotovosti

Trajalo je nekaj let, vendar je Heisenbergu uspelo dokazati načelo negotovosti, ki pravi, da Δx × Δp = h/2, kar je število, ki izhaja iz prvotnih enačb, vendar izpusti π in i, ki sta povezana s faznimi spremembami. Heisenberg je pojasnil, da je svoje načelo negotovosti izpeljal iz tega prejšnjega rezultata, ko je leta 1927 napisal članek, v katerem je predstavil to teorijo.

Konstanta, zapisana h, imenovana Planckova konstanta, je skrivnostno število, ki se pogosto pojavlja, zato moramo razumeti, kaj je to majhno število. Številčno je običajno podana kot 6,62607×10^-34 J s (joule sekund). Gre torej za količino, ki vključuje energijo in čas.

Odkrita je bila, ko je Planck ugotovil, da se energija popolnega sevalca (imenovanega sevalec črnega telesa) oddaja v enotah določene velikosti, imenovanih "kvanti" (ednina te besede je "kvant"). Izsevana energija se oddaja kot fotoni, frekvenca fotona pa je sorazmerna z "udarcem", ki ga odda. Različne frekvence vidne svetlobe doživljamo kot različne barve. Na vijoličnem koncu spektra ima vsak foton relativno veliko energije, na rdečem koncu spektra pa ima vsak foton relativno majhno količino energije. Količino energije fotona lahko izračunamo z enačbo E = hν (energija je enaka Planckovi konstanti, pomnoženi z "nu" ali frekvenco).

Heisenbergovo načelo negotovosti Δx × Δp ≥ h nam pove, da se lahko vedno, ko skušamo določiti določene pare števil, le približamo in da če skušamo enega od njih natančneje določiti, tj. če skušamo Δx zmanjšati, da bi imeli boljšo predstavo o položaju nečesa, potem bomo morali za drugo število v paru dobiti nazaj večje število in da je količina, za katero se razlikujeta, tesno povezana s h.

Drug par fizikalnih količin je v skladu z razmerjem negotovosti: ΔE × Δt ≥ h, in ta par med drugim kaže, da če pogledamo v medzvezdni prostor, nekam, kjer ne bi pričakovali, da bomo sploh kaj našli, in Δt vedno bolj zmanjšujemo na 0, potem mora biti ΔE vedno večji, da bi ohranili ravnovesje, prikazano v enačbi - in nenadoma lahko nekaj z zagonom nastane le za to kratko obdobje.

Kako razložiti to nedoločenost (pomanjkanje gotovosti)? Kaj se dogaja v vesolju? Pogosto je rečeno, da lahko nova teorija, ki je uspešna, zagotovi nove informacije o preučevanih pojavih. Heisenberg je ustvaril matematični model, ki je napovedal pravilne intenzitete za spekter svetlih črt vodika, vendar je, ne da bi to nameraval storiti, odkril, da nekateri pari fizikalnih količin razkrivajo nepričakovano negotovost. Do tistega trenutka nihče ni imel pojma, da meritev ni mogoče v nedogled narediti vedno bolj natančnih in točnih. Dejstvo, da jih ni mogoče narediti bolj zanesljive, bolj natančne, je bilo osupljivo novo odkritje. Mnogi ljudje tega niso bili pripravljeni sprejeti.

Bohr in njegovi kolegi so trdili, da fotoni, elektroni itd. nimajo ne lege ne zagona, dokler jih ne izmerimo. To teoretično stališče je izhajalo iz odkritja negotovosti in ni bilo le nekakšna osebna preferenca glede tega, v kaj verjeti. Bohr je dejal, da o nečem, kot je foton ali elektron, ne vemo ničesar, dokler tega ne opazujemo. Da bi lahko opazovali tako majhno stvar, moramo z njo nekako sodelovati. V vsakdanjem življenju je mogoče narediti nekaj takega, kot je hoja ob avtomobilu, pri čemer si beležimo, kdaj avtomobil prečka točke na mreži, narisani na pločniku. Morda bo sama teža avtomobila pritisnila na majhne vzvode v pločniku, ki bodo izklopili ure, pritrjene na vsakega od njih, in zabeležili težo avtomobila. Na koncu bi imeli jasen zapis o tem, kje se je avtomobil nahajal ob različnih časih, lahko pa bi izračunali tudi smer njegovega napredovanja in težo. Tako bi lahko v vsakem trenutku na uri vedeli za njegov položaj in njegov zagon (hitrost, pomnožena z maso). Ne bi si niti predstavljali, da bi sila, potrebna za premikanje majhnih vzvodov, kakor koli vplivala na napredovanje avtomobila. Prav tako si ne bi predstavljali, da avtomobil med točkami na pločniku, kjer so vzvodi, nima nobene lege ali trajektorije ali da avtomobil v tistih trenutkih obstaja v nekakšni tridimenzionalni megli in se umiri le, ko pritiska na vzvod. Svet, ki ga poznamo, ne razkriva teh nenavadnih vrst interakcij.

Za lociranje ladje na morju v najtemnejši noči bi lahko uporabili reflektor in ta svetloba ne bi motila položaja ali smeri potovanja ladje, vendar bi bilo za lociranje elektrona s svetlobo treba vanj udariti z enim ali več fotoni, od katerih ima vsak dovolj zagona, da bi motil položaj in trajektorijo elektrona. Iskanje elektrona z drugimi sredstvi bi zahtevalo njegovo fizično omejitev, ki bi prav tako prekinila njegovo gibanje naprej.

Če želimo locirati foton, ga lahko brez prekinitve njegovega gibanja naprej spravimo skozi krožno luknjo v pregradi. Če poznamo čas, ko je bil foton oddan (na primer z laserjem), in čas, ko foton prispe do detekcijskega zaslona, kot je digitalni fotoaparat, je mogoče izračunati čas, potreben za prepotovanje te razdalje, in čas, v katerem je foton prehajal skozi luknjo. Vendar mora imeti okrogla luknja premer večji od velikosti fotona, da lahko foton preide skozi njo. Manjša ko je krožna luknja, bližje smo poznavanju natančnega položaja fotona, ko gre skozi njo. Vendar pa nikoli ne moremo vedeti, ali je foton v tistem trenutku izven središča. Če je luknja natanko enako velika kot foton, ne bo šel skozi. Z zmanjševanjem premera luknje se vedno bolj spreminja gibalna sila ali smer fotona, ko zapušča luknjo.

Niels Bohr in njegovi kolegi so trdili, da se znajdemo v velikih težavah, če za stvari, ki so premajhne, da bi jih lahko videli celo z mikroskopom, predpostavljamo, da so resnične, kar imamo dokazano le na ravni vsakdanjega življenja. V vsakdanjem življenju imajo stvari v vsakem trenutku določen položaj. Na atomskem merilu nimamo nobenega dokaza, ki bi podpiral to ugotovitev. V vsakdanjem življenju imajo stvari določen čas, v katerem se pojavijo. Na atomski lestvici nimamo dokazov, ki bi podpirali ta sklep. Če v vsakdanjem življenju opazujemo tovarno od nočne izmene prvega dne do dnevne izmene drugega dne in vidimo, kako se končni avtomobil pripelje na transportni dok, bi bilo nesmiselno reči, da ni mogoče ugotoviti, ali je bil dostavljen med nočno ali dnevno izmeno. Na atomski ravni pa lahko pokažemo primere, ko moramo en sam foton šteti, kot da je bil proizveden v dveh časovnih obdobjih. (Če to ni dovolj hudo, lahko pokažemo tudi primere, ko je en sam foton proizveden z dvema sosednjima laserjema.)

Del težav pri ugotavljanju dogajanja na atomski ravni je v tem, da bi radi vedeli, kje se nekaj nahaja in kakšna je njegova trajektorija, ter da bi oboje vedeli istočasno, vendar ne moremo hkrati izmeriti položaja in trajektorije. Zato bodisi naenkrat izmerimo gibalno moč fotona ali elektrona in nato brez večjih zamud, kot je potrebno, izmerimo njegov položaj, ali pa stvari zamenjamo in najprej izmerimo položaj, nato pa gibalno moč. Težava je v tem, da s tem, ko prva meritev dobi precej določeno obliko (tako, da jo na nek način stisnemo navzdol), povečamo negotovost pri naslednji meritvi. Če so bile naše začetne meritve tako grobe, da je bilo v vsako od njih vnesenih veliko napak, potem bi lahko stvari izboljšali tako, da bi pri vsaki od njih uporabili lažji dotik, vendar nikoli ne bi mogli preseči določene meje natančnosti.

Iz vsakdanjega življenja vemo, da bodo rezultati tehtanja na kopalniški tehtnici, ki je postavljena na pralni stroj v ciklu vrtenja, netočni, saj se bo igla na tehtnici močno zibala. Pralni stroj lahko izklopimo. Za zelo natančne meritve pa lahko ugotovimo, da igla tehtnice niha tudi zaradi vožnje tovornjakov v bližini, zato lahko tehtnico postavimo na nekaj, kar jo izolira pred zunanjimi motnjami. Verjamemo, da lahko vibracije odpravimo do te mere, da bodo rezultati tako natančni, kot želimo. Nikoli ne pomislimo, da stvar na tehtnici sama vibrira ali da ima nedoločen gibalni moment.

Če izhajamo iz načela negotovosti, se zdi, da za nobeno stvar na atomski ravni dejansko ni določenega položaja in zagona ter da lahko eksperimentatorji le prisilijo stvari v določljivost v mejah, ki jih določa načelo negotovosti. Bohr in njegovi kolegi so trdili le, da brez meritev ne moremo vedeti ničesar, in ko so meritve opravljene, lahko stvari potisnemo v smer bolj določenega položaja ali bolj določenega zagona, vendar ne moremo doseči absolutne določenosti ali gotovosti, ki bi si jo želeli. Drugi pa so to možnost vzeli resno in trdili, da če je matematika pravilna, potem v svetu ultra majhnega ne more biti dokončnosti ali gotovosti. Narava znanosti je takšna, da je matematika le model resničnosti in ni nobenega zagotovila, da je to pravilen model.

Matematika in praktične posledice stvari, ki jih matematika napoveduje, so tako zanesljive, da se je z njimi zelo težko ne strinjati, vendar pa je iz matematike o resničnem svetu nastalo več različnih idej. Med znanstveniki, ki so sodelovali z Nielsom Bohrom v Københavnu, je načelo negotovosti pomenilo, da fizično vesolje na elementarni ravni ne obstaja v deterministični obliki. Namesto tega je zbirka verjetnosti ali potencialov.

V nasprotju z zgodbo, ki jo je okoli matematike spletla kopenhagenska skupina, obstajajo tudi druge zgodbe, kot je "interpretacija več vesolij", ki pravi, da se vsakič, ko je v skladu s kvantno teorijo možnih več rezultatov, vsak rezultat pojavi v svojem novem vesolju. Einstein je trdil, da več možnih izidov ne obstaja, zato obstaja samo eno vesolje in je determinirano, ali, kot je dejal, "Bog se ne igra s kockami".

Če bi bila h najmanjša možna količina energije, potem se osnovna enačba, ki prikazuje energijo, ki jo vsebujejo fotoni različnih frekvenc, ne bi uravnotežila. Bila bi napačna.

Ugovori proti načelu negotovosti

Albert Einstein je uvidel, da nova kvantna mehanika predvideva pomanjkanje položaja in zagona v času pred izvedbo meritev, zato je temu odločno nasprotoval. Trdno je verjel, da so stvari imele določene položaje in določene momente, preden so bile izmerjene, in da dejstvo, da izmerimo eno od para stvari in oviramo možnost natančnega izmerjanja druge, ne dokazuje, da pred tem ni bilo nobenega od njiju. Skupaj z dvema kolegoma je napisal dokument, ki je postal znan kot "EPR dokument". Ta članek trdi, da morajo obstajati lastnosti, ki določajo položaj in gibanje, in da če jih lahko vidimo ali če lahko dobimo informacije o njih, potem lahko matematično poznamo in predvidimo položaj in gibanje. Dolgo časa so ljudje mislili, da ni mogoče dokazati ali ovreči tega, kar je bilo za Einsteina vera. Spor je bil zelo produktiven, saj je pripeljal do vseh sodobnih dosežkov na področju prepletanja.

Matematično je bilo dokazano, da se je Einstein motil. Leta 1964 je John Stewart Bell razvil matematično metodo za razlikovanje med obnašanjem dveh delcev, ki imata determinirana stanja, ki so neznana le dvema posameznikoma, ki ju raziskujeta, in dveh delcev, ki imata prepletena stanja, ki so nedoločljiva ali negotova, dokler jih ne izmerimo. Njegova metoda pokaže, da so verjetnosti za pridobitev določenih rezultatov ob dveh različnih predpostavkah različne. Njegovo delo se imenuje Bellov teorem ali Bellova neenakost. Poskusi so pokazali, da se narava obnaša tako, kot jo opisuje Bell.

Druga pot do negotovosti

Prve razprave o Heisenbergovem načelu negotovosti so temeljile na modelu, ki ni upošteval, da imajo delci snovi, kot so elektroni, protoni itd., valovno dolžino. Leta 1926 je Louis de Broglie pokazal, da imajo vse stvari, ne le fotoni, svojo frekvenco. Stvari imajo valovno in delčno naravo, tako kot fotoni. Če bi poskušali valovanje stvari, kot je proton, narediti ožje in višje, bi bila njegova lega jasnejša, vendar bi bil potem gibalni moment slabše opredeljen. Če bi poskušali del valovnega opisa, ki se nanaša na gibalno moč, narediti jasnejši, tj. da bi ostal v ožjem območju vrednosti, bi se vrh vala razširil in njegov položaj bi postal manj določen.

Val, ki je del opisa fotona, v kvantni mehaniki ni ista stvar kot val na površini oceana ali območja stisnjenega in redkega zraka, ki sestavljajo zvočne valove. Namesto tega imajo ti valovi vrhove ali območja z visoko amplitudo, ki so povezani z verjetnostjo, da na tej točki v prostoru in času nekaj najdemo. Natančneje, kvadrat amplitude je tisti, ki določa verjetnost, da se bo pojavil nek pojav.

Val, ki velja za foton, je lahko čisti sinusni val. V tem primeru bi kvadrat vrednosti vsakega vrha podal verjetnost opazovanja fotona v tej točki. Ker so amplitude sinusnih valov povsod enake, bi bila verjetnost za najdbo fotona na vsakem od njih enaka. Praktično gledano torej poznavanje valovanja za enega od teh fotonov ne bi dalo namiga, kje ga iskati. Po drugi strani pa je zagon fotona matematično povezan z amplitudo njegovega valovanja. Ker imamo v tem primeru čisti sinusni val, je amplituda vsakega cikla valovanja enaka, zato je s tem valovanjem povezana samo ena vrednost momenta. Ne bi vedeli, kam bo foton udaril, vedeli pa bi natančno, kako močno bo udaril.

Pri svetlobnih snopih, ki se osredotočijo na neko točko na detekcijskem zaslonu, valovi, povezani s fotoni, niso čisti sinusni valovi. Namesto tega gre za valove z visoko amplitudo v eni točki in veliko nižjimi amplitudami na obeh straneh tega najvišjega vrha. Matematično je mogoče takšno valovanje analizirati na več različnih sinusnih valov različnih valovnih dolžin. Nekoliko lažje si je predstavljati obratni potek tega procesa, če si ogledamo začetni sinusni val ene frekvence, ki mu dodamo drugi sinusni val drugačne valovne dolžine, nato tretji, četrti in tako naprej. Rezultat bo kompleksni val, ki bo imel en visok vrh in bo vseboval veliko število valov različnih valovnih dolžin in s tem različnih momentov. V tem primeru je verjetnost, da se bo foton pojavil v določeni točki, izjemno velika, vendar se lahko izkaže, da je njegov gibalni moment povezan z valovno dolžino katerega koli od sestavnih valov. Z drugimi besedami, vrednost p = ħ/λ ni več ena sama vrednost, saj je treba upoštevati vse dolžine sestavljenih "valov različnih valovnih dolžin".

Simulacija prikazuje, kako matematično modelirati izostritev lokacije delca: Na prvotni sinusni val se nanese več različnih valovnih oblik. Središče bo tvorilo vedno višji vrh, število ostalih vrhov pa se bo povečalo, vendar se bo njihova višina zmanjšala, ker bodo interferirali drug z drugim. Tako je na koncu v superpoziciji veliko različnih valov, vsak z različno valovno dolžino in (po p = ħ/λ) različnim momentom, vendar le en zelo visok vrh, ki postaja vse višji in ožji ter nam daje nekaj, kar je vse bližje določenemu položaju.

Da bi bil zagon vedno bolj določen, bi morali odstranjevati vedno več nadgrajenih sinusnih valov, dokler nam ne bi ostal le še preprost sinusni val. Pri tem bi postopoma zmanjševali višino osrednjega vrha in postopoma povečevali višine konkurenčnih mest, kjer bi lahko našli delec.

Ko začnemo z valovno sliko subatomskih delcev, imamo običajno vedno opravka z razmeroma visokimi osrednjimi vrhovi in razmeroma veliko valovnimi dolžinami komponent. V takšnih okoliščinah nikoli ne bo mogoče napovedati natančnega položaja ali natančnega zagona. Če je matematični model natančen prikaz resničnega sveta, potem noben foton ali drug subatomski delec nima natančnega položaja ali določenega navora. Ko merimo takšen delec, lahko izberemo metodo, ki še bolj stisne vrh in ga zoži, ali pa izberemo metodo, ki vrh zniža in izravna valovne dolžine komponent. Glede na to, kaj merimo in kako merimo, lahko dosežemo, da bo naša lokacija bolj določena, ali pa da bo območje gibanja ožje. Pri načrtovanju poskusa lahko pazimo, da se izognemo različnim načinom pretresanja aparature, vendar se ne moremo znebiti dejstva, da na začetku ni bilo nič povsem določenega.

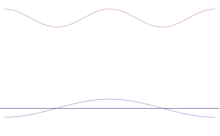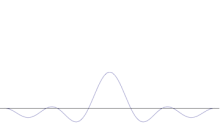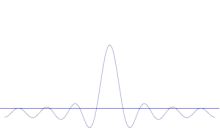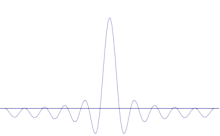
Superpozicija več ravninskih valov. Valovni paket se z dodajanjem več valov vedno bolj lokalizira. Fourierova transformacija je matematična operacija, ki valovni paket razdeli na posamezne ravninske valove. Upoštevajte, da so tukaj prikazani valovi realni le za ponazoritev, medtem ko je v kvantni mehaniki valovna funkcija na splošno kompleksna.

Kulturni vplivi

Heisenbergovo načelo negotovosti je najbolj vplivalo na argumente o svobodi volje. Po teorijah klasične fizike je mogoče trditi, da so zakoni vzroka in posledice neizprosni in da je mogoče iz tega začetnega stanja izračunati interakcije vseh snovi in energije, ki se bodo pojavile v prihodnosti, ko se bo vesolje začelo na določen način. Ker je vse absolutno posledica tistega, kar je bilo pred tem, so trdili, da je bila vsaka odločitev človeka in vsaka situacija, v katero se znajde, vnaprej določena že od začetka časa. Potemtakem nimamo nobene izbire pri tem, kaj počnemo.

Ljudje, ki verjamejo v svobodo volje, trdijo, da zakoni kvantne mehanike ne predvidevajo, kaj se bo zgodilo, temveč le, kaj je bolj in kaj manj verjetno. Zato je vsako dejanje rezultat vrste naključnih "metov kovanca" in nobene odločitve ni mogoče povezati z nizom nujnih predpogojev.

Izraza "kvantni skok" in "kvantni skok" sta postala običajna načina govorjenja o stvareh. Običajno želijo ljudje nekaj opisati kot veliko spremembo, ki se zgodi v kratkem časovnem obdobju. Izraz se dejansko uporablja za obnašanje elektrona v atomu, ko absorbira foton, ki prihaja od zunaj, in tako preskoči z ene orbite okoli atomskega jedra na višjo orbito ali ko odda foton in tako pade z višje orbite na nižjo orbito. Neils Bohr in njegovi sodelavci so menili, da se elektron ne giblje med orbitami, temveč izgine z ene orbite in se v trenutku pojavi na drugi orbiti. Kvantni preskok torej v resnici ni nekakšna pretresljiva sprememba, temveč nenadna majhna sprememba iz enega področja v drugo.

Ko ljudje merijo nek proces na subatomski ravni in se pokaže načelo negotovosti, lahko rečemo, da je človek s svojim delovanjem vplival na merjeno stvar. Izvedba meritve, katere namen je dobiti natančen podatek o položaju delca, bo neizogibno vplivala na njegov gibalni moment in ne glede na to, kaj se stori, da se ta gibalni moment izmeri čim prej po izmeri njegovega položaja, se verjetnost tega, kakšen gibalni moment bo odkrit, ne more ne spremeniti. Tako lahko načelo negotovosti pojasni nekatere vrste motenj, ki jih povzročajo preiskovanci in ki vplivajo na rezultate poskusa ali opazovanja. Vendar pa vsi učinki opazovalcev niso posledica kvantnih učinkov ali načela negotovosti. Preostali so "učinki opazovalca", ne pa učinki kvantne negotovosti.

Učinki opazovalcev vključujejo vse vrste stvari, ki delujejo na običajni človeški ravni dogodkov. Če antropolog poskuša dobiti jasno predstavo o življenju v primitivni družbi, vendar njegova prisotnost vznemirja skupnost, ki jo obiskuje, so lahko njegova opažanja zelo zavajajoča. Vendar nobena od pomembnih interakcij ne poteka na ravni, ki jo opisuje kvantna mehanika ali načelo negotovosti.

Včasih se beseda "kvantni" uporablja v oglaševalske namene za označevanje nečesa novega in zmogljivega. Proizvajalec majhnih bencinskih motorjev Briggs and Stratton ima na primer linijo štirivaljnih motorjev z majhno močjo za bencinske kosilnice in podobno vrtno orodje, ki jo imenuje "Quantum".

Več branja

• Predstavitev kvantne teorije, str. 115 in 158

J.P. McEvoy in Oscar Zarate