Minkowskijev prostorski čas: definicija, metrična signatura in pomen

Prostorski čas Minkowskega je v posebni teoriji relativnosti štiridimenzionalna mnogoterost, ki jo je ustvaril Hermann Minkowski. Ima štiri dimenzije: tri dimenzije prostora (x, y, z) in eno dimenzijo časa. Prostorski čas Minkowskega ima metrično signaturo (-+++) in opisuje ravno površino, kadar ni prisotne mase. V tem članku se običajno imenuje prostorski čas Minkowskega preprosto prostorski čas.

Prostorski čas Minkowskega pa velja le v posebni teoriji relativnosti. Splošna relativnost uporablja pojem ukrivljenega prostor-časa za opis učinkov gravitacije in pospešenega gibanja.

Metrična signatura in metrični tenzor

Ključni matematični objekt v Minkowskijevem prostorskem času je metrični tenzor η (eta), ki v koordinatah (t, x, y, z) z izbiro signature (-+++) zapišemo kot diagonalen matriks η_{μν} = diag(-1, 1, 1, 1). To pomeni, da je invarinantna razdalja (interval) med dvema dogodkoma Δx^μ = (c Δt, Δx, Δy, Δz) dana z izrazom

s^2 = η_{μν} Δx^μ Δx^ν = -c^2 Δt^2 + Δx^2 + Δy^2 + Δz^2.

V fiziki se pogosto uporabi naravna izbira enot c = 1, kar poenostavi zapise (s^2 = -Δt^2 + Δx^2 + Δy^2 + Δz^2). Pomembno je, da se izbira predznaka (na primer (+---) namesto (-+++)) šteje le za konvencijo in ne spreminja fizičnih posledic, čeprav vpliva na oblike enačb.

Tipi intervalov in posledice

Časovni (timelike): če je s^2 < 0 (pri signaturi -+++). Tedaj obstaja inercialni opazovalec, za katerega sta dogodka v istem mestu prostora, in med njima lahko potuje snov s hitrostjo manjšo od svetlobe. Za timelike interval je mogoče definirati lastni čas τ, povezan z intervalom: τ = (1/c) sqrt(-s^2).
Prostorski (spacelike): če je s^2 > 0. Takšni dogodki niso v vzročno-posledični zvezi; ni mogoče, da bi signal z omejeno hitrostjo c povezal dogodka. Različni inercialni opazovalci lahko dogodka štejejo za vzporedna v času (različnost simultanosti).
Nikčen (lightlike ali null): če je s^2 = 0. To opisuje poti svetlobe in drugih brezmasnih delcev, ki potujejo s hitrostjo c. Takšne razdalje določajo stožec svetlobe (light cone) iz vsakršnega dogodka.

Stožec svetlobe, vzročnost in Lorentzove transformacije

Stožec svetlobe iz točke loči dogodke, ki so v prihodnosti ali preteklosti in so z njo vzročeno povezani, od dogodkov, ki so zunaj dosega (prostorsko ločeni). Lorentzove transformacije so linearne preslikave med inercialnimi opazovalci, ki ohranjajo interval s^2; to je matematična predstavitev homogenosti in izotropnosti Minkowskijevega prostora v posebni relativnosti. Ohranjanje intervala zagotavlja, da vsi inercialni opazovalci enako sklenemo o tem, ali je razlika med dogodkoma časovna, prostorska ali ničelna.

Geometrijski pomen in fizikalne posledice

Minkowskijev prostor je ravna (flat) pseudo-Riemannova mnogoterost z ničelno krivino (Riemannov tenzor je enak nič). Zato so geodezije (potovanja brez zunanjih sil) v takšnem prostoru ravne črte — to ustreza Newtonovemu stanju enakomisnosti v inercialnih okvirih.
Lastni čas τ, ki ga meri uro, potujoča skupaj z delcem, je geodetska dolžina njegovih časovnih svetovnih črt in je fizikalno merljiv kvantitet. To pojasni učinke, kot sta dilatacija časa in relativistični časovni pomik v eksperimentih s hitrimi delci in natančnimi urami.
Minkowskijeva geometrija omogoča tudi poenoten opis prostora in časa: mnoge (prej ločene) fizikalne enačbe dobijo simetrično relativistični obliko, na primer elektromagnetizem v obliki Lorentz-invariantnih enačb.

Povezava s splošno relativnostjo

Prostorski čas Minkowskega velja za model brez gravitacije in za regije, kjer so učinki gravitacije zanemarljivi. Splošna relativnost ta model razširi tako, da metriko (ki je v Minkowskiju konstantna) naredi odvisno od položaja — metriki so sedaj poljubne simetrične tenzorje g_{μν}(x) in prostor-čas je lahko ukrivljen zaradi prisotnosti mase in energije. Kljub temu ostaja Minkowskijev prostorski čas pomemben kot lokalna tangentna aproksimacija ukrivljenega prostor-časa: v majhnih območjih vsake točke ukrivljen prostorski čas vidimo kot približno Minkowskijev.

Uporabnost in vizualizacija

Za razumevanje osnovnih konceptov relativnosti so koristni Minkowskijevi diagrame (čas-prostor grafi), kjer je ena os čas, druga pa ena izmed prostorskih smeri. Takšni diagrami jasneje prikažejo stožec svetlobe, svetovne črte opazovalcev in posledice relativne simultanosti. Minkowskijev formalizem je tudi osnova za kvantno polje v ravnem prostor-času in za razumevanje simetrij (Lorentzova simetrija, translacije), ki vodijo do ohranitvenih zakonov v relativističnih teorijah.

Na kratko: Minkowskijev prostorski čas je preprosta, a temeljna geometrijska postavka posebne relativnosti. Metrična signatura (-+++) določa, kako se čas razlikuje od prostora, ohranjanje intervala s^2 pod Lorentzovimi transformacijami zagotavlja vzročnost in enotnost fizikalnih zakonov za vse inercialne opazovalce, medtem ko splošna relativnost to shemo razširi na ukrivljene prostor-čase, kjer gravitacija predstavlja ukrivitev metrike.

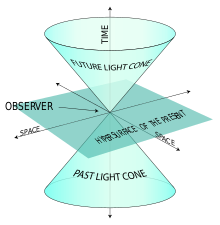
Primer svetlobnega stožca.

Opredelitev(e)

Matematični

Prostorski čas si lahko predstavljamo kot štiridimenzionalni koordinatni sistem, v katerem so osi podane z

( c t , x , y , z ) {\displaystyle (ct,x,y,z)} $(ct,x,y,z)$

Označimo jih lahko tudi z

( x 1 , x 2 , x 3 , x 4 ) {\displaystyle (x_{1},x_{2},x_{3},x_{4})} $(x_{1},x_{2},x_{3},x_{4})$

Pri čemer x 1 {\displaystyle x_{1}} $x_{1}$ predstavlja c t {\displaystyle ct} $ct$ . Razlog za merjenje časa v enotah svetlobne hitrosti, pomnožene s časovno koordinato, je v tem, da so enote za čas enake enotam za prostor. Prostor-čas ima diferencial za dolžino loka, ki je podan z

d s 2 = - c 2 d t 2 + d x 2 + d y 2 + d z 2 {\displaystyle ds^{2}=-c^{2}dt^{2}+dx^{2}+dy^{2}+dz^{2}}} $ds^{2}=-c^{2}dt^{2}+dx^{2}+dy^{2}+dz^{2}$

To pomeni, da ima prostor-čas metrični tenzor, ki je podan z

g u v = [ - 1 0 0 0 0 0 1 0 0 0 0 1 0 0 0 0 0 0 1 ] {\displaystyle g_{uv}={\begin{bmatrix}-1&0&0&0&0\0&1&0&0&0\0&0&1&0\0&0&0&0&1\end{bmatrix}}} $g_{uv}={\begin{bmatrix}-1&0&0&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\end{bmatrix}}$

Kot smo že omenili, je prostor-čas povsod raven; do neke mere si ga lahko predstavljamo kot ravnino.

Enostavno

Prostor-čas si lahko predstavljamo kot "prizorišče", na katerem se odvijajo vsi dogodki v vesolju. Vse, kar potrebujemo za določitev točke v prostor-času, sta določen čas in značilna prostorska orientacija. Štiri dimenzije si je težko (praktično nemogoče) predstavljati, vendar lahko z uporabo spodnje metode naredimo nekaj analogij.

Diagrami prostor-časa

Hermann Minkowski je uvedel določeno metodo za izdelavo grafov koordinatnih sistemov v prostor-času Minkowskega. Kot vidimo desno, se različni koordinatni sistemi ne strinjajo glede prostorske orientacije in/ali časovnega položaja predmeta. Kot je razvidno iz diagrama, obstaja samo ena prostorska os (os x) in ena časovna os (os ct). Po potrebi lahko uvedemo dodatno prostorsko dimenzijo (os y); žal pa je to meja števila dimenzij: izrisovanje grafov v štirih dimenzijah je nemogoče. Pravilo za izdelavo grafov v prostor-času Minkowskega je naslednje:

1) Kot med osjo x in osjo x'je podan s t a n ( α ) = v c {\displaystyle tan(\alpha )={\frac {v}{c}}} $tan(\alpha )={\frac {v}{c}}$ kjer je v hitrost predmeta

2) Hitrost svetlobe skozi prostor-čas vedno tvori kot 45 stopinj z vsako od osi.

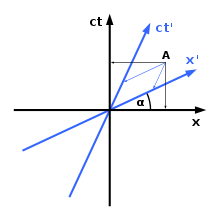
V teoriji relativnosti oba opazovalca dogodek v točki A pripisujeta različnim časom.

Prostorski čas v splošni teoriji relativnosti

V splošni teoriji relativnosti je Einstein uporabil enačbo

R u v - 1 2 g u v R = 8 π T u v {\displaystyle R_{uv}-{\frac {1}{2}}g_{uv}R=8\pi T_{uv}} $R_{uv}-{\frac {1}{2}}g_{uv}R=8\pi T_{uv}$

Da bi omogočili, da se prostor-čas dejansko ukrivi; posledica tega so učinki gravitacije.

Sorodne strani

Nadzor organa

BNF: cb11979629v (podatki)
GND: 4293944-6

Vprašanja in odgovori

V: Kaj je prostor-čas Minkowskega?

O: Prostorski čas Minkowskega je štiridimenzionalna mnogoterost, ki jo je ustvaril Hermann Minkowski. Ima tri razsežnosti prostora (x, y, z) in eno razsežnost časa.

V: Kakšna je metrična signatura prostor-časa Minkowskega?

O: Metrični podpis prostorčasa Minkowskega je (-+++).

V: Kako prostor-čas Minkowskega opisuje ravno površino?

O: Kadar ni mase, prostor-čas Minkowskega opisuje ravno površino.

V: Ali se prostor-čas Minkowskega uporablja za splošno relativnost?

O: Ne, Minkowskega prostor-čas velja samo za posebno relativnost. Splošna relativnost uporablja pojem ukrivljenega prostor-časa za opis učinkov gravitacije in pospešenega gibanja.

V: Koliko dimenzij ima prostor-čas Minkowskega?

O: Minkowsijev prostor-čas ima štiri dimenzije - tri dimenzije prostora (x, y, z) in eno dimenzijo časa.

V: Kdo je ustvaril koncept Minkowsijevega prostor-časa?

O: Hermann Minkowksi je ustvaril koncept prostorskega časa MInkowskega.