Nomogram (izravnalni diagram): kaj je, zgodovina in praktična uporaba
Nomogram ali izravnalni diagram ali abaque je graf za izračun. To je dvodimenzionalni diagram, ki prikazuje izračun matematične funkcije. Nomogrami so zasnovani tako, da z enostavno geometrijsko operacijo (navadno položitvijo ravnila) omogočajo hitro odčitavanje vrednosti neznane spremenljivke brez računalnika ali kalkulatorja.
Področje nomografije je leta 1884 izumil francoski inženir Philbert Maurice d'Ocagne (1862–1938). Dolga leta se je uporabljala za hitre grafične izračune zapletenih formul za inženirje. Nomogrami namesto standardnih kartezičnih koordinat uporabljajo vzporedni koordinatni sistem, ki ga je izumil d'Ocagne. V 20. stoletju so bili nomogrami razširjeni v številnih panogah — inženiringu, pomorstvu, vojski, medicini in kemiji — saj so omogočali hitro polje-uporabne izračune tudi v terenskih pogojih.
Kako deluje nomogram
Nomogram sestavlja niz n lestvic, po ena za vsako spremenljivko v enačbi. Če poznamo vrednosti n−1 spremenljivk, lahko ugotovimo vrednost neznane spremenljivke ali pa s fiksiranjem vrednosti nekaterih spremenljivk preučujemo razmerje med nefiksiranimi spremenljivkami. Rezultat dobimo tako, da položimo ravnilo čez znane vrednosti na lestvicah in odčitamo neznano vrednost na mestu, kjer prečka lestvico za to spremenljivko. Navidezna ali narisana črta, ki jo ustvari ravnilo, se imenuje indeksna črta ali izopleta.
Vrste nomogramov in lestvic
- Linearni nomogrami: vsebujejo ravne vzporedne lestvice; najpogostejši za preproste večspremenljivostne enačbe.
- Logaritmični nomogrami: uporabljajo logaritmične lestvice za pretvorbo množenja in deljenja v seštevanje in odštevanje ter so primerni za produktne enačbe.
- Krogni (cirkularni) nomogrami: lestvice so razporejene po obodu kroga — včasih bolj kompaktni za določene tipe računov.
- Posebne lestvice: lahko vključujejo reciproke, kvadratne ali trigonometrične lestvice, odvisno od oblike funkcije, ki jo želimo prikazati.
Izdelava in načelo konstrukcije
Osnovna ideja pri konstrukciji nomograma je transformacija matematične relacije v geometrijsko razmerje, kjer imajo položaji točk na posameznih lestvicah takšna razmika, da so vse točke, katerih spremenljivke zadoščajo enačbi, poravnane z ravno črto. Pri tem se pogosto uporablja logaritmična transformacija ali drugačna linearizacija (npr. za racionalne ali potencne funkcije). Klasični koraki:
- Analiza enačbe in izbira transformacij (log, recipročna, kvadratna itd.),
- Določitev obsega vsake lestvice glede na praktične vrednosti spremenljivk,
- Preslikava funkcije v razmike na lestvicah tako, da bo povezava med njimi linijska,
- Preizkus natančnosti in morebitna kalibracija za zmanjšanje napak pri odčitavanju.
Praktična uporaba
Nomogrami so bili široko uporabljeni pred razmahom elektronskih kalkulatorjev in računalnikov, še vedno pa imajo praktične uporabe:
- hitri terenski izračuni brez električne energije,
- navodila in delovni listi v industriji in laboratorijih,
- medicina — nomogrami za odmerjanje zdravil, izračun telesne površine ali tveganja pri določenih stanjih,
- radiotehnika in telekomunikacije — npr. Smithov diagram (soroden pristop za analizo impedanc),
- izobraževanje — vizualna pomoč za razumevanje odvisnosti med spremenljivkami in transformacij.
Prednosti in omejitve
- Prednosti: enostavna uporaba z ravnilom, hitri rezultati, intuitivna vizualizacija odnosov, neodvisnost od električne energije.
- Omejitve: omejena natančnost zaradi gostote lestvic in napak pri odčitavanju ter paralakse, težje razširljiv pri velikem številu spremenljivk, zahtevna natančna izdelava za kompleksne funkcije.
Primer (poenostavljeno)
Za enačbo c = a × b je najlažji nomogram z uporabo logaritmov: na treh vzporednih logaritemsko razporejenih lestvicah postavimo vrednosti log(a), log(b) in log(c). Ravnilo, položeno skozi točki za a in b, bo sekalo lestvico c pri vrednosti, ki ustreza produktu a in b. Tak pristop s transformacijo množenja v seštevanje je klasičen primer, kako nomogram poenostavi račun.
Sodobni razvoj
Danes se nomogrami pogosto digitalno reproducirajo v obliki spletnih aplikacij ali programskih orodij, ki samodejno generirajo grafične izračune in omogočajo boljšo natančnost ter interaktivnost. Kljub temu ostajajo klasični papirni nomogrami uporabna rešitev tam, kjer je potrebna hitra vizualna ocena ali delovanje brez elektrike.
Nomografi so torej preprost, a premišljen grafični pripomoček za praktične izračune: združujejo matematično transformacijo z enostavno geometrijo in so bili pomemben tehnološki korak v razvoju inženirskih in znanstvenih orodij.
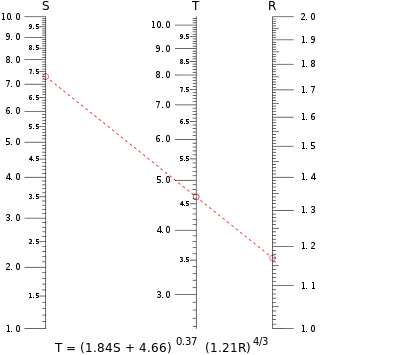
Tipičen nomogram v vzporednem merilu. V tem primeru je izračunana vrednost T, ko sta v enačbo vstavljena S = 7,30 in R = 1,17. Izopleta prečka lestvico za T pri vrednosti malo manj kot 4,65.
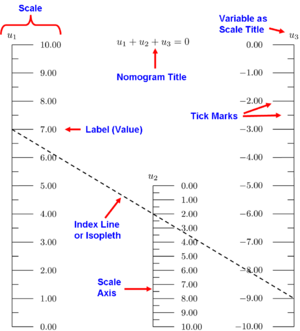
Sestavni deli nomograma v vzporednem merilu
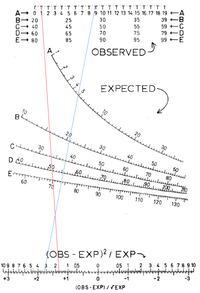
Nomogram porazdelitve Chi-kvadrat
Uporaba
Nomogrami so se pogosto uporabljali približno 75 let. Omogočali so hitre in natančne izračune pred dobo žepnih kalkulatorjev. Rezultate iz nomograma dobimo hitro in zanesljivo, če narišemo eno ali več črt. Uporabniku ni treba znati reševati algebrskih enačb, iskati podatkov v tabelah, uporabljati drsnika ali vnašati števil v enačbe, da bi dobil rezultate. Uporabniku niti ni treba poznati osnovne enačbe, ki jo nomogram predstavlja.
Nomogrami imajo v svoji zasnovi znanje o domeni. Na primer, za oblikovanje večjih nomogramov za večjo natančnost nomograf običajno vključi le območja lestvic, ki so smiselna in zanimiva za problem. Številni nomogrami vključujejo tudi druge uporabne oznake, kot so referenčne oznake in barvna območja. Vse to uporabniku zagotavlja uporabna vodila.
Nomogram je podobno kot drsnik grafična analogna računska naprava. Podobno kot pri drsniku je njegova natančnost omejena z natančnostjo, s katero je mogoče narisati, reproducirati, pregledati in poravnati fizične oznake.Drsnik je računalo za splošne namene, nomogram pa je zasnovan za izvajanje posebnih izračunov. Nomograme je še vedno mogoče uporabiti za preverjanje odgovora iz drugega, natančnejšega izračuna, ki pa je morda nagnjen k napakam.
Vprašanja in odgovori
V: Kaj je nomogram?
O: Nomogram je graf, ki se uporablja za izračun in prikazuje izračun matematične funkcije.
V: Kdo je izumil področje nomografije?
O: Področje nomografije je leta 1884 izumil Philbert Maurice d'Ocagne, francoski inženir.
V: Kakšen je bil namen nomogramov?
O: Nomogrami so se dolga leta uporabljali za hitre grafične izračune zapletenih formul.
V: Iz koliko lestvic je sestavljen nomogram?
O: Nomogram je sestavljen iz n lestvic, po ena za vsako spremenljivko v enačbi.
V: Kako lahko z nomogramom ugotovimo vrednost neznane spremenljivke?
O: Če poznamo vrednosti n-1 spremenljivk, lahko vrednost neznane spremenljivke ugotovimo tako, da položimo ravnilo čez znane vrednosti na lestvicah in odčitamo neznano vrednost tam, kjer se križa z lestvico za to spremenljivko.
V: Kako se imenuje navidezna ali narisana črta, ki jo ustvari ravnilo?
O: Virtualna ali narisana črta, ki jo ustvari ravnilo, se imenuje indeksna črta ali izopleta.
V: Katera vrsta koordinatnega sistema se uporablja v nomogramih?
O: Pri nomogramih se namesto standardnih kartezičnih koordinat uporablja vzporedni koordinatni sistem, ki ga je izumil d'Ocagne.
