Verjetnostni prostor
Verjetnostni prostor je matematični model, ki se uporablja za opis znanstvenih poskusov Verjetnostni prostor je sestavljen iz treh delov:
- Vzorčni prostor, v katerem so navedeni vsi možni izidi
- Niz dogodkov. Vsak dogodek povezuje nič ali več izidov
- Funkcija, ki vsakemu dogodku pripiše verjetnost.
Rezultat je rezultat ene same izvedbe modela. Ker so posamezni izidi morda malo uporabni v praksi, se za opisovanje skupin izidov uporabljajo kompleksnejši dogodki. Zbirka vseh takih dogodkov je σ-algebra F {\displaystyle \scriptstyle {\mathcal {F}}} 
. Nazadnje je treba za vsak dogodek določiti verjetnost, da se bo zgodil. To storimo z uporabo funkcije mere verjetnosti, P.
Ko je prostor verjetnosti določen, se predpostavlja, da "narava" naredi svojo potezo in izbere en izid, ω, iz vzorčnega prostora Ω. Za vse dogodke v F {\displaystyle \scriptstyle {\mathcal {F}}}, ki vsebujejo izbrani izid ω (spomnimo se, da je vsak dogodek podmnožica Ω), pravimo, da so se "zgodili". Izbira, ki jo opravi narava, je izvedena tako, da bi se, če bi poskus ponovili neskončno velikokrat, relativne frekvence pojavljanja vsakega od dogodkov ujemale z verjetnostmi, ki jih predpisuje funkcija P.
Ugledni sovjetski matematik Andrej Kolmogorov je v tridesetih letih prejšnjega stoletja uvedel pojem verjetnostnega prostora skupaj z drugimi aksiomi verjetnosti.
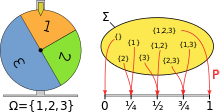
Modeliranje kolesa sreče z uporabo verjetnostnega prostora
Vprašanja in odgovori
V: Kaj je verjetnostni prostor?
O: Verjetnostni prostor je matematični model, ki se uporablja za opis znanstvenih poskusov. Sestavljen je iz treh delov: vzorčnega prostora, ki navaja vse možne izide, množice dogodkov, ki povezujejo nič ali več izidov, in funkcije, ki vsakemu dogodku pripiše verjetnost.
V: Iz česa je sestavljen vzorčni prostor?
O: Vzorčni prostor je sestavljen iz vseh možnih izidov, pogosto zapisanih kot Ω {\displaystyle \Omega } , izid pa kot ω {\\displaystyle \Omega } .
V: Kaj je izid?
O: Izid je rezultat ene same izvedbe modela.
V: Za kaj se uporabljajo dogodki v verjetnostnih prostorih?
O: Dogodki se uporabljajo za opisovanje skupin izidov, saj posamezni izidi morda niso praktično uporabni. Zbirko vseh takih dogodkov imenujemo σ-algebra, včasih zapisana kot F {\displaystyle {\mathcal {F}}}.
V: Kako so vsakemu dogodku dodeljene verjetnosti?
O: Verjetnosti se vsakemu dogodku pripišejo z uporabo funkcije verjetnostne mere P.
V: Kdo je uvedel pojem verjetnostnih prostorov? O: Znani sovjetski matematik Andrej Kolmogorov je v tridesetih letih prejšnjega stoletja skupaj z drugimi aksiomi verjetnosti uvedel pojem verjetnostnih prostorov.
