Konjugirane spremenljivke v kvantni mehaniki — definicija, enačbe in primeri

Konjugirane spremenljivke v kvantni mehaniki: jasna definicija, Heisenberg‑Bornove enačbe (Q, P), izračuni in praktični primeri za študente in raziskovalce.

Konjugirane spremenljivke so posebni pari spremenljivk (na primer položaj x in gibalna količina p), katerih zaporedje pri uporabi določenih matematičnih operacij vpliva na rezultat. To pomeni, da operatorja oziroma matriki Q in P iz kvantne mehanike običajno ne komutirata: QP ni enako PQ. Pri tem * ne pomeni navadnega množenja realnih števil, ampak zaporedno delovanje operatorjev (kompozicijo operatorjev oziroma produkt matrik ali operatorjev v prostoru stanj).

Heisenbergova matrična mehanika in pomen P ter Q

Fizik Werner Heisenberg je v klasifikaciji kvantnih pojavov uvedel pristop, ki danes imenujemo matrična mehanika. V njem so fizične količine predstavljene kot matrike ali operatorji, katerih množenje ni nujno komutativno. Heisenberg je pri tem prepoznal, da sta gibalna količina (masa krat hitrost, pogosto označena z P) in položaj (označen z Q) konjugirani spremenljivki — torej velja, da P*Q ≠ Q*P v splošnem.

Matrične enačbe in primeri povezanosti stanj

V matrični formulaciji lahko elemente produktov operatorjev zapišemo kot vsote po vmesnih stanjih. V članku so navedeni dve posebej uporabni enačbi za izračun elementov produktov komponent gibalne količine in položaja — natančneje produktov matrik p in q med stanji, ki jih označimo z indeksi:

S prvo enačbo lahko ugotovimo produkt gibalne sile in položaja:

Y ( n , n - b ) = ∑ a p ( n , n - a ) q ( n - a , n - b ) {\displaystyle Y(n,n-b)=\sum _{a}^{}\,p(n,n-a)q(n-a,n-b)}

Drugo enačbo lahko uporabimo za izračun produkta položaja in navora:

Z ( n , n - b ) = ∑ a q ( n , n - a ) p ( n - a , n - b ) {\displaystyle Z(n,n-b)=\sum _{a}^{}\,q(n,n-a)p(n-a,n-b)}

Tu indeksi n, n−a, n−b označujejo kvantna stanja (na primer energijska nivoja atoma). Vsota po a pomeni vsoto po vseh mogočih vmesnih stanjih, kar je matematični izraz za dejstvo, da produkt dveh operatorjev vključuje prispevek vseh poti med začetnim in končnim stanjem.

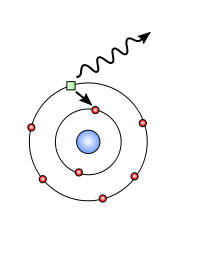
V konkretni fizikalni situaciji, na primer pri opisovanju atoma vodika, so takšne matrike in njihovi produkti neposredno povezani z verjetnostmi prehodov med energetskimi stanji in s frekvenčnimi komponentami valovnih funkcij. Pri padcu elektrona iz višjega v nižji orbitalni nivo se odda foton — slika prikazuje ta proces:

Komutator in kanonična relacija

Nekaj časa po Heisenbergu so matematični pomen in splošnost nekomutativnosti raziskovali drugi fiziki in matematikarji. Max Born (skupaj s Pascualom Jordanom in drugimi) je pomagal utemeljiti matematično strukturo ter pokazal, da je razlika med Q*P in P*Q fizično pomembna. Ta razlika se pogosto označuje kot komutator in zapišemo jo kot [Q,P] = QP − PQ.

V izvorni formulaciji članka je zapisana relacija:

Q ∗ P - P ∗ Q = i h 2 π {\displaystyle {Q*P-P*Q={\frac {ih}{2\pi }}}}

V sodobni in običajni zapisu to zapišemo krajše kot [Q,P] = iħ, kjer je ħ = h / (2π) zvezdica Planckove konstante. Simbol i označuje enoto imaginarnega števila, i pa pomeni, da so operatorji običajno linearni operatorji na kompleksnem vektorskem prostoru stanj. (Simboli: Q je matrika oziroma operator položaja, P je matrika oziroma operator gibanja, h pa je Planckova konstanta.)

Posledice nekomutativnosti

• Heisenbergov negotovostni princip: Nekomutativnost konjugiranih operatorjev je matematična osnova negotovostnega odnosa. Za položaj in gibalno količino velja omejitev za razpršenosti meritev: Δx · Δp ≥ ħ/2. To pomeni, da ne moremo hkrati poljubno natančno izmeriti obeh količin.
• Kvantizacija gibanja: Kanonične konjugirane spremenljivke vodijo k diskretnim energijskim nivojem v vezanih sistemih (npr. atomskih orbitali, harmoničnem oscillatorju), ker so operatorji omejeni in imajo diskretne spektralne komponente.
• Različne fizikalne primere: Poleg položaja in gibalne količine (q,p) so konjugirani pari tudi faza in število fotonov v kvantni optiki, kot tudi pravila za kotni moment in kotne spremenljivke v rotacijskih problemih. Poseben primer je tudi par energija–čas, pri katerem je interpretacija nekoliko drugačna zaradi posebnosti časa kot parametra v kvantni mehaniki.

Dodatna pojasnila in zgodovinski kontekst

Heisenbergova matrična mehanika in Schrödingerjeva valovna mehanika sta različni matematični formulaciji iste teorije — kvantne mehanike — in dajeta enake fizikalne napovedi. Born, Heisenberg in Jordan so razvili formalizem, ki je pokazal, kako iz klasčnih spremenljivk z uporabo zamenjave Poissonovih zank v kvantni različici pride do komutatorjev operatorjev. Born je bil tudi pomemben pri interpretaciji kvantnih verjetnosti (Bornovo pravilo), ki povezuje elemente valovne funkcije z verjetnostjo izida meritve.

Kje se uporabljajo konjugirane spremenljivke

Konjugirane spremenljivke so temeljna orodja v fiziki, kemiji (npr. kvantna kemija pri opisu elektronov v molekulah), kvantni optiki, trdno stanje fizike in pri številnih drugih področjih znanosti in tehnologije (npr. kvantno računalništvo). Njihova nekomutativnost ima neposredne posledice za konstrukcijo Hamiltoniana sistema, za spektre energij in za način, kako se izvajajo meritve na kvantnih sistemih.

Če želite razumeti podrobnejše matematične dokaze in izpeljave (npr. kako [Q,P]=iħ vodi do negotovostnega odnosa ali kako se izrazita kvantizacija pojavi pri harmoničnem oscilatorju), je priročno nadaljevati z učenjem linearne algebra operatorjev, spektralne teorije in osnov kvantne mehanike (operaterski formalizem, Hilbertov prostor, eigene vrednosti in eigenvektorji).

Vprašanja in odgovori

V: Kaj so konjugirane spremenljivke?

V: Kdo je odkril konjugirane spremenljivke?

V: S katero enačbo lahko izračunamo produkt gibalne sile in položaja?

V: S katero enačbo lahko izračunamo produkt položaja in navora?

V: Kaj je Max Born odkril o konjugiranih spremenljivkah?

V: Kako se Planckova konstanta pojavlja v kvantni mehaniki?

V: Na katerih področjih se uporabljajo konjugirane spremenljivke?

Išči po črki