Fourierova transformacija
Fourierova transformacija je matematična funkcija, s katero lahko poiščemo osnovne frekvence, ki sestavljajo signal ali valovanje. Če na primer zaigramo akord, lahko zvočni val akorda prenesemo v Fourierovo transformacijo in tako ugotovimo, iz katerih not je akord sestavljen. Izhodni rezultat Fourierjeve transformacije se včasih imenuje frekvenčni spekter ali porazdelitev, ker prikazuje spekter frekvenc vhoda. Ta funkcija se pogosto uporablja v kriptografiji, oceanografiji, strojnem učenju, radiologiji, kvantni fiziki ter pri oblikovanju in vizualizaciji zvoka.
Fourierova transformacija funkcije f ( x ) {\displaystyle f(x)}
je podana z
F ( α ) = ∫ - ∞ + ∞ f ( x ) e - 2 π i α x d x {\displaystyle F(\alpha )=\int _{-\infty }^{+\infty }f(x)e^{-2\pi i\alpha x}dx} 
α {\displaystyle \alpha } 
je frekvenca
F ( α ) {\displaystyle F(\alpha )}
je funkcija Fourierjeve transformacije in vrne vrednost, ki predstavlja, kako razširjena je frekvenca α {\displaystyle \alpha } v izvirnem signalu.
e - 2 π i α x {\displaystyle e^{-2\pi i\alpha x}} 
Predstavlja ovijanje vhodne funkcije f ( x ) {\displaystyle f(x)} okoli izvora v kompleksni ravnini pri neki frekvenci α {\displaystyle \alpha }
Inverzna Fourierova transformacija je podana z
f ( x ) = ∫ - ∞ + ∞ F ( α ) e + 2 π i x α d α {\displaystyle f(x)=\int _{-\infty }^{+\infty }F(\alpha )e^{+2\pi ix\alpha }d\alpha } 
Fourierova transformacija pokaže, katere frekvence so v signalu. Na primer, poglejmo zvočni val, ki vsebuje tri različne glasbene note: Če naredimo graf Fourierjeve transformacije tega zvočnega vala (s frekvenco na osi x in intenzivnostjo na osi y), bomo pri vsaki frekvenci videli vrh, ki ustreza eni od glasbenih not.
Številne signale lahko ustvarimo s seštevanjem kosinusov in sinusov z različnimi amplitudami in frekvencami. Fourierova transformacija prikazuje amplitude in faze teh kosinusov in sinusov glede na njihove frekvence.
Fourierjeve transformacije so pomembne, ker so številni signali bolj smiselni, če so njihove frekvence ločene. V zgornjem primeru zvočnega signala ob pogledu na signal glede na čas ni jasno, da so v signalu note A, B in C. Številni sistemi delajo različne stvari na različnih frekvencah, zato lahko tovrstne sisteme opišemo s tem, kaj delajo na posamezni frekvenci. Tak primer je filter, ki blokira visoke frekvence.
Za izračun Fourierjeve transformacije je potrebno razumevanje integracije in imaginarnih števil. Za računanje Fourierovih transformacij za vse, razen za najpreprostejše signale, se običajno uporabljajo računalniki. Hitra Fourierova transformacija je metoda, ki jo računalniki uporabljajo za hitro izračunavanje Fourierove transformacije.
· 
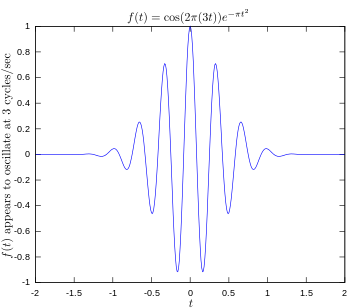
Izvirna funkcija prikazuje signal, ki niha pri 3 hercih.
· 
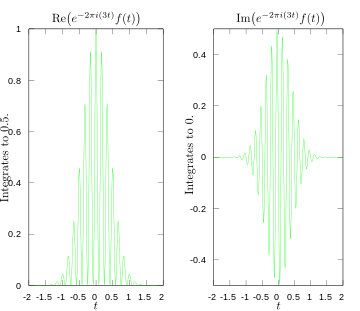
Realni in imaginarni del integranda za Fourierovo transformacijo pri 3 hercih
· 
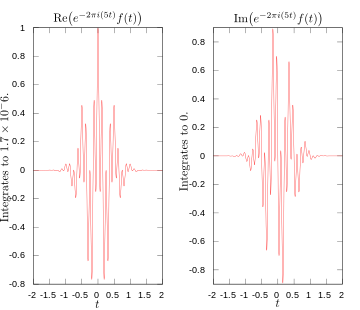
Realni in imaginarni del integranda za Fourierovo transformacijo pri 5 hercih
· 
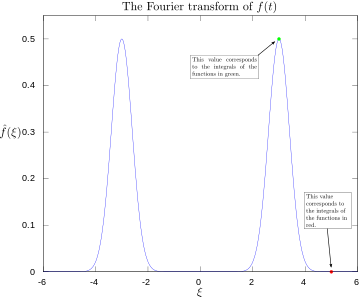
Fourierjeva transformacija z označenimi 3 in 5 herci.
Vprašanja in odgovori
V: Kaj je Fourierova transformacija?
O: Fourierova transformacija je matematična funkcija, ki jo lahko uporabimo za iskanje osnovnih frekvenc, iz katerih je sestavljeno valovanje. Z njo lahko iz kompleksnega valovanja poiščemo frekvence, ki ga sestavljajo, in tako določimo note, ki sestavljajo akord.
V: Katere so nekatere uporabe Fourierjeve transformacije?
O: Fourierova transformacija se velikokrat uporablja v kriptografiji, oceanografiji, strojnem učenju, radiologiji, kvantni fiziki ter pri oblikovanju in vizualizaciji zvoka.
V: Kako se izračuna Fourierova transformacija?
O: Fourierova transformacija funkcije f(x) je podana s F(ב) = ∫-∞+∞f(x)e-2נiבxdx, kjer je ב frekvenca. To vrne vrednost, ki predstavlja, kako razširjena je frekvenca ב v izvirnem signalu. Inverzna Fourierova transformacija je podana s f(x) = ∫-∞+∞F(ב)e+2נixבdב.
V: Kako je videti izhod Fourierove transformacije?
O: Izhod Fourierjeve transformacije lahko imenujemo frekvenčni spekter ali porazdelitev, ker prikazuje porazdelitev možnih frekvenc vhoda.
V: Kako računalniki izračunavajo hitre Fourierove transformacije?
O: Računalniki uporabljajo algoritem, imenovan hitra Fourierova transformacija (FFT), da hitro izračunajo vse, razen najpreprostejših transformacij signalov.
V: Kaj nam pogled na signale glede na čas ne pokaže?
O: Če gledamo signale glede na čas, nam ni jasno, katere note so v njih prisotne; mnogi signali so bolj smiselni, če njihove frekvence ločimo in jih analiziramo posamično.
