Frekvenčna porazdelitev v statistiki: definicija, primeri in tabele
V statistiki je frekvenčna porazdelitev seznam vrednosti spremenljivke v vzorcu. Običajno gre za seznam, urejen po količini — prikazuje, kolikokrat se posamezna vrednost pojavi (absolutna frekvenca). Pogosto prikazujemo tudi relativne frekvence (deleže) in kumulativne frekvence, ker so bolj primerne za primerjave med vzorci različnih velikosti.
Osnovne vrste frekvenc
- Absolutna frekvenca (f) — število opazovanj z določeno vrednostjo ali v določenem razredu.
- Relativna frekvenca (p) — delež vseh opazovanj: p = f / N (pogosto izraženo v %: 100·f/N), kjer je N velikost vzorca.
- Kumulativna frekvenca (F) — vsota absolutnih frekvenc do določene vrednosti ali razreda: F_i = f_1 + f_2 + ... + f_i.
- Kumulativna relativna frekvenca — F_i / N, uporabna za oceno porazdelitve do določene meje (npr. kvantili, mediana).
Kdaj uporabiti negrupirano in kdaj grupirano tabelo
Če spremenljivka zavzema majhno število ločenih vrednosti (npr. odgovori na Likertovi lestvici), lahko sestavimo negrupirano frekvenčno tabelo, kjer vsaka vrednost dobi svojo vrstico. Če pa spremenljivka zavzema zvezne vrednosti ali je število možnih vrednosti zelo veliko (npr. višina v cm, dohodki), je smiselno vrednosti združiti v intervale (razrede) in sestaviti grupirano frekvenčno tabelo.
Kako sestavimo frekvenčno tabelo
- Za negrupirano tabelo: preštejemo pojavitve vsake vrednosti in izračunamo relativne ter kumulativne frekvence.
- Za grupirano tabelo:
- izberemo število razredov (k) in širino razreda (h);
- razrede definiramo tako, da pokrijejo celoten obseg podatkov (npr. od najmanjše do največje vrednosti);
- preštejemo opazovanja v vsakem razredu (f_i) ter izračunamo p_i = f_i/N in kumulativne frekvence.
Priporočila za število razredov: pogosto uporabljeni pristopi so Sturgesovo pravilo k ≈ 1 + 3,322·log10(N) ali približno k ≈ sqrt(N). To so zgolj smernice; pri velikih vzorcih lahko uporabimo več razredov, pri malih manj.
Tipične tabele — primeri
Primer 1: odgovori 100 ljudi na petstopenjsko Likertovo lestvico (1 = močno strinjam, 5 = močno se ne strinjam). Predpostavimo števila odgovorov:
| Ocena | Absolutna frekvenca (f) | Relativna frekvenca (p) |
|---|---|---|
| 1 | 20 | 20 % |
| 2 | 25 | 25 % |
| 3 | 30 | 30 % |
| 4 | 15 | 15 % |
| 5 | 10 | 10 % |
| Skupaj | 100 | 100 % |
Ta preprosta tabela je jasna in uporabna, kadar so vrednosti diskretne in jih ni veliko.
Primer 2: višine 30 učencev (grupirana frekvenčna tabela). Predpostavimo razrede po 10 cm:
| Razred (cm) | Absolutna frekvenca (f) | Relativna frekvenca (p) | Kumulativna frekvenca (F) |
|---|---|---|---|
| 150–159 | 4 | 13,3 % | 4 |
| 160–169 | 12 | 40,0 % | 16 |
| 170–179 | 10 | 33,3 % | 26 |
| 180–189 | 4 | 13,3 % | 30 |
| Skupaj | 30 | 100 % | 30 |
Iz grupirane tabele lahko ocenimo osnovne statistike. Če želimo oceno povprečja iz grupiranih podatkov, uporabimo sredine razredov (m_i) in približno oceno: povprečje ≈ (Σ m_i·f_i) / N. Pri zgornjem primeru so sredine: 154.5, 164.5, 174.5, 184.5; izračun povprečja z njimi da hitro približek dejanskega povprečja.
Vizualizacije frekvenčnih porazdelitev
- Histogram — stolpični prikaz frekvenc za razrede; za zvezne spremenljivke predstavlja osnovno vizualno orodje.
- Stolpični diagram — za diskretne vrednosti (npr. Likert).
- Frekvenčni poligon — povezane točke, uporabno za primerjavo dveh porazdelitev.
- Ogiva (kumulativna krivulja) — prikazuje kumulativne frekvence, uporabna za oceno kvantilov.
- Stem-and-leaf — ohranja surove vrednosti, koristen za manjše n in za hitro pregledovanje oblike porazdelitve.
Uporaba frekvenčnih porazdelitev
- Opis podatkov: hitra ocena, kje se nahaja jedro porazdelitve, ali je porazdelitev enakomerno razporejena ali zgoščena.
- Osnova za izračun statistik: povprečje, mediana, modus, varianca pri skupinah (približno iz grupiranih podatkov).
- Prepoznavanje nenavadnih vrednosti (outlierjev) in oblikovanje hipotez.
- Vizualizacija in komunikacija rezultatov (poročila, predstavitve).
Pasti in priporočila
- Preširoki razredi lahko skrijejo pomembne značilnosti porazdelitve; preozki razredi lahko ustvarijo "šum".
- Pri definiranja meja razredov bodimo dosledni glede vključenosti meja (npr. ali je meja vključno levo ali desno) in to jasno zapišimo.
- Pri majhnih vzorcih je smiselno raje uporabiti negrupirane podatke ali malo razredov, da se izognemo pretirani diskretizaciji.
- Vedno preverimo, ali je bolj informativno prikazati absolutne frekvence ali relativne (pri primerjavi vzorcev različnih velikosti so relativne nujne).
Zaključek
Frekvenčna porazdelitev je osnovno, a ključno orodje za opisovanje in razumevanje podatkov. S pravilno izbiro obliko tabele ali grafičnega prikaza lahko hitro povemo, kje je jedro porazdelitve, kakšna je razpršenost in kateri deli razporeditve zahtevajo nadaljnjo pozornost. Pri obdelavi zveznih podatkov pazimo na način grupiranja in upoštevajmo vpliv odločitev (število razredov, širina razredov, vključenost meja) na interpretacijo rezultatov.
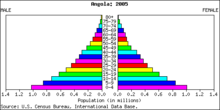
Primer (absolutne) frekvenčne porazdelitve. To je piramida prebivalstva Angole za leto 2005.
To je prebivalstvena piramida Kitajske za leto 2005.
Aplikacije
Upravljanje in delovanje s podatki v frekvenčnih tabelah je veliko preprostejše od delovanja z neobdelanimi podatki. Obstajajo preprosti algoritmi za izračun mediane, povprečja (statistike), standardnega odklona itd. iz teh tabel.
Testiranje statističnih hipotez temelji na oceni razlik in podobnosti med frekvenčnimi porazdelitvami. Ta ocena vključuje mere osrednje tendence ali povprečja, kot sta povprečje in mediana, ter mere variabilnosti ali statistične razpršenosti, kot sta standardni odklon ali varianta.
Za poševno porazdelitev pogostosti pravimo, da je poševna, če sta njena srednja vrednost in mediana različni. Kurtoza frekvenčne porazdelitve je koncentracija rezultatov na sredini ali vrh porazdelitve, če jo prikažemo grafično - na primer v histogramu. Če je porazdelitev z večjim vrhom kot normalna porazdelitev, pravimo, da je leptokurtična; če je z manjšim vrhom, pravimo, da je platikurtična.
Frekvenčne porazdelitve se uporabljajo tudi pri frekvenčni analizi za razbijanje šifer in se nanašajo na relativno pogostost črk v različnih jezikih.
Vprašanja in odgovori
V: Kaj je frekvenčna porazdelitev?
O: Frekvenčna porazdelitev je seznam vrednosti, ki jih ima spremenljivka v vzorcu, razvrščenih po številu. Prikazuje, kolikokrat se pojavi posamezna vrednost.
V: Kako bi lahko izgledala frekvenčna porazdelitev odgovorov na petstopenjski Likertovi lestvici?
O: Frekvenčna porazdelitev odgovorov na petstopenjski Likertovi lestvici je lahko videti kot preprosta tabela, ki prikazuje število ljudi, ki so ocenili vsako točko na lestvici.
V: Kateri sta dve pomanjkljivosti uporabe te vrste tabele?
O: Dve slabosti uporabe te vrste tabel sta, da je to lahko težko ali celo nemogoče, kadar gre za zvezne vrednosti ali kadar je možnih vrednosti preveč.
V: V čem je ta shema drugačna, kadar imamo opravka z zveznimi vrednostmi ali velikim številom možnih vrednosti?
O: Kadar gre za zvezne vrednosti ali veliko število možnih vrednosti, se lahko namesto tega uporabi nekoliko drugačna shema, ki temelji na razponu vrednosti.
V: Kako bi lahko izgledala frekvenčna tabela za višino učencev?
O: Tabela pogostosti za višino učencev lahko prikaže območja in koliko učencev spada v posamezno območje.
V: Katere informacije zagotavlja frekvenčna porazdelitev?
O: Frekvenčna porazdelitev zagotavlja informacije o tem, kako pogosto se določene spremenljivke pojavljajo v vzorcih in kako so porazdeljene po teh vzorcih.
