Standardni odklon – pomen, izračun in primeri razpršenosti podatkov
Razlaga standardnega odklona: pomen, izračun, vzorčni primeri in uporaba pri analiziranju razpršenosti podatkov, napak in tveganj s praktičnimi primeri.
Standardni odklon je število, ki pove, kako so posamezne meritve v skupini razpršene okoli povprečja ali pričakovane vrednosti. Majhen standardni odklon pomeni, da je večina vrednosti blizu povprečja, velik standardni odklon pa kaže, da so podatki bolj razpršeni. Standardni odklon je ena od osnovnih statistik za opis razpršenosti podatkov in se pogosto uporablja v znanosti, financah in vsakdanjih analizah podatkov.
Zakaj kvadriramo in potem korenimo?
Pri izračunu standardnega odklona najprej izračunamo odklone posameznih vrednosti od povprečja, jih kvadriramo (da odpravimo negativne predznake), nato izračunamo povprečje teh kvadratov (to imenujemo varianca) in na koncu vzamemo kvadratni koren, da dobimo standardni odklon. Tako dobimo mersko enoto, ki je enaka enoti izvornih podatkov (npr. kilogrami, točke, evri).
Populacijski in vzorčni standardni odklon
Obstajata dve pogosti različici standardnega odklona:
- Populacijski standardni odklon (ko imamo podatke za celotno populacijo):
σ = sqrt( (1/N) * Σ (xi − μ)² ), kjer je N velikost populacije, μ pa populacijsko povprečje. - Vzorčni standardni odklon (ko imamo vzorec iz večje populacije):
s = sqrt( (1/(n−1)) * Σ (xi − x̄)² ). V imenovalcu uporabimo (n−1) (Besselova korekcija), da je ocena variance in standardnega odklona nepristranska glede na populacijo.
Koraki za izračun vzorčnega standardnega odklona
- Izračunajte aritmetično sredino vzorca x̄ = (Σ xi) / n.
- Za vsako opazovanje izračunajte odmik od povprečja (xi − x̄) in ga kvadrirajte.
- Seštejte vse kvadrate odmikov: Σ (xi − x̄)².
- Delite s (n − 1) in izračunajte kvadratni koren rezultata: s = sqrt(Σ (xi − x̄)² / (n − 1)).
Primer izračuna
Podatki: 2, 4, 4, 4, 5, 5, 7, 9
- Povprečje (μ ali x̄) = (2+4+4+4+5+5+7+9) / 8 = 5
- Vsakega odstopanja kvadriramo in seštejemo: Σ (xi − 5)² = 32
- Populacijska varianca = 32 / 8 = 4 → populacijski σ = sqrt(4) = 2
- Vzorčna varianca = 32 / (8 − 1) = 32 / 7 ≈ 4,571 → vzorčni s ≈ 2,14
Interpretacija in pravilo 68–95–99,7
Če podatki sledijo normalni (Gaussovi) porazdelitvi, velja približno:
- ~68 % vrednosti je znotraj ±1 σ okoli povprečja,
- ~95 % vrednosti je znotraj ±2 σ,
- ~99,7 % vrednosti je znotraj ±3 σ.
Ta pravila omogočajo hitro oceno, ali je posamezna mera izstopajoča ali ne. V praksi znanstveniki pogosto poročajo povprečje ± standardni odklon ali uporabijo 1,96·σ za približno 95 % interval, če gre za normalno porazdelitev.
Razlika med standardnim odklonom in standardno napako
V besedilu je omenjena "stopnja napake", ki je včasih navedena kot dvakratnik standardnega odklona. Treba je ločiti dve pojmovanji:
- Standardni odklon (SD) opisuje razpršenost posameznih opazovanj v podatkih.
- Standardna napaka povprečja (SE) = SD / sqrt(n) opisuje negotovost ocene povprečja. Približno 95‑% interval zaupanja za povprečje je x̄ ± 1,96·SE (pogosto zaokroženo kot ±2·SE).
Uporabe in omejitve
- Uporabno v znanosti: Znanstveniki pogosto poročajo o standardnem odklonu, da pokažejo razpršenost meritev okoli povprečja.
- V financah: standardni odklon donosnosti pomeni tveganje ali nihajnost vračanja naložbe (denar).
- Pri delu s vzorci: pogosto lahko merimo le vzorec in uporabimo vzorčni standardni odklon kot oceno populacijskega.
- Omejitve: standardni odklon je občutljiv na odstopanja in asimetrične porazdelitve. V takih primerih so uporabne robustne mere razpršenosti (npr. interkvartilno razpon, median absolute deviation).
Praktični nasveti
- Vedno preverite porazdelitev podatkov (graf histograma ali boxplot). Če je porazdelitev močno poševna ali vsebuje izstopajoče vrednosti, uporabite robustne mere.
- Pri poročanju rezultatov jasno navedi, ali gre za populacijski ali vzorčni standardni odklon.
- Ne zamenjujte SD in SE; vsak ima drugačen pomen in uporabo v interpretaciji rezultatov.
Standardni odklon je torej osnovno orodje za razumevanje, koliko se podatki razlikujejo od povprečja. Pravilna uporaba in razlaga standardnega odklona omogoča boljše razumevanje negotovosti in variabilnosti v podatkih.
.png)
Graf normalne porazdelitve (ali zvonaste krivulje). Vsak barvni pas ima širino enega standardnega odklona.
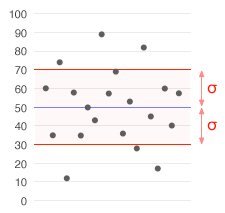
Podatkovni niz s povprečjem 50 (prikazano modro) in standardnim odklonom (σ) 20.
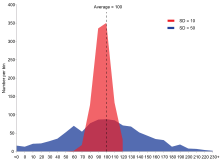
Primer dveh vzorčnih populacij z enakim povprečjem in različnimi standardnimi odkloni. Rdeča populacija ima povprečje 100 in SD 10; modra populacija ima povprečje 100 in SD 50.
Osnovni primer
Razmislite o skupini z naslednjimi osmimi številkami:
2 , , 44, 4, 5, , 5, 7{\displaystyle9 2,\ 4,\ 4,\ 4,\ 5,\ 5,\ 7,\ 9}
Povprečje teh osmih števil je 5:
2 + +4 +4 +4 + + 5+ + 5+ 7= 98{\displaystyle5 {\frac {2+4+4+4+5+5+7+9}{8}}=5}
Če želite izračunati standardni odklon populacije, najprej ugotovite razliko vsakega števila na seznamu od povprečja. Nato rezultat vsake razlike izračunajte s kvadratom:
( 2- 5) =2 ( - 3) =2 (95 - 5) =2 = 02( 04-5 ) =2 ( - 1) =2 (15 - ) = ( - 5) =2 = 02( 04-5 ) =2 ( - 1) =2 (17 - 5) = 222( 44-5 ) = ( - ) = 2( -1 ) = 2( 19- 5) =2 = 42{\displaystyle16 {\begin{array}{lll}(2-5)^{2}=(-3)^{2}=9&&(5-5)^{2}=0^{2}=0\\(4-5)^{2}=(-1)^{2}=1&&(5-5)^{2}=0^{2}=0\\(4-5)^{2}=(-1)^{2}=1&&(7-5)^{2}=2^{2}=4\\(4-5)^{2}=(-1)^{2}=1&&(9-5)^{2}=4^{2}=16\\\end{array}}}
Nato poiščite povprečje teh vrednosti (vsoto delite s številom števil). Na koncu izračunajte kvadratni koren:
( +9 +1 +1 +1 + + 0+ 0+ 4) 16= 8{\displaystyle2 {\sqrt {\frac {(9+1+1+1+1+0+0+0+4+16)}{8}}}=2}
Odgovor je standardni odklon populacije. Formula je pravilna le, če je osem številk, s katerimi smo začeli, celotna skupina. Če so le del naključno izbrane skupine, potem moramo v spodnjem delu (imenovalcu) predzadnjega koraka uporabiti 7 (ki je n - 1) namesto 8 (ki je n). Potem je odgovor vzorčni standardni odklon. To se imenuje Besselov popravek.
Več primerov
Nekoliko težji primer iz resničnega življenja: Povprečna višina odraslih moških v Združenih državah Amerike je 70 cm, standardni odklon je 3 cm. Standardni odklon 3" pomeni, da je večina moških (približno 68 %, če predpostavimo normalno porazdelitev) za 3" višja do 3" nižja od povprečne višine (67"-73") - en standardni odklon. Skoraj vsi moški (približno 95 %) so za 6 cm višji do 6 cm nižji od povprečja (64-76 cm) - dva standardna odklona. Trije standardni odkloni vključujejo vse številke za 99,7 % preučevane vzorčne populacije. To velja, če je porazdelitev normalna (v obliki zvona).
Če bi bil standardni odklon enak nič, bi bili vsi moški visoki natanko 70 cm. Če bi bil standardni odklon 20 cm, bi bili nekateri moški precej višji ali nižji od povprečja, običajno v razponu od 50 do 90 cm.
Drug primer: vsaka od treh skupin {0, 0, 14, 14}, {0, 6, 8, 14} in {6, 6, 8, 8} ima povprečje (sredino) 7. Njihovi standardni odkloni pa so 7, 5 in 1. Tretja skupina ima veliko manjši standardni odklon kot drugi dve, saj so vsa njena števila blizu 7. Osnovna ideja je, da nam standardni odklon pove, kako daleč od povprečja so ostala števila. Ima enake enote kot sama števila. Če je na primer skupina {0, 6, 8, 14} starost skupine štirih bratov v letih, je povprečje 7 let, standardni odklon pa 5 let.
Standardni odklon lahko služi kot merilo negotovosti. V znanosti na primer standardni odklon skupine ponavljajočih se meritev pomaga znanstvenikom ugotoviti, kako gotovi so glede povprečnega števila. Pri odločanju, ali se meritve iz poskusa ujemajo z napovedjo, je standardni odklon teh meritev zelo pomemben. Če je povprečno število iz poskusov preveč oddaljeno od napovedanega števila (pri čemer se razdalja meri v standardnih odklonih), potem preizkušena teorija morda ni pravilna. Glej interval napovedi.
Primeri uporabe
Razumevanje standardnega odklona niza vrednosti je koristno za to, da veste, kako velika je pričakovana razlika od "povprečja" (sredine).
Vreme
Kot preprost primer si oglejte povprečne dnevne temperature dveh mest, enega v notranjosti države in drugega v bližini oceana. Koristno je razumeti, da je razpon dnevnih visokih temperatur za mesta blizu oceana manjši kot za mesta v notranjosti države. Ti dve mesti imata lahko enako povprečno dnevno visoko temperaturo. Vendar bo standardni odklon dnevne visoke temperature za obalno mesto manjši kot za mesto v notranjosti države.
Šport
Druga možnost je, da si ogledamo športne ekipe. V vsakem športu obstajajo ekipe, ki so v nekaterih stvareh dobre, v drugih pa ne. Ekipe, ki so uvrščene najvišje, ne bodo pokazale velikih razlik v sposobnostih. V večini kategorij jim gre dobro. Nižji kot je standardni odklon njihovih sposobnosti v vsaki kategoriji, bolj uravnotežene in dosledne so. Ekipe z višjim standardnim odklonom pa bodo manj predvidljive. Ekipa, ki je običajno slaba v večini kategorij, bo imela nizek standardni odklon. Ekipa, ki je običajno dobra v večini kategorij, bo prav tako imela nizek standardni odklon. Ekipa z visokim standardnim odklonom pa je lahko ekipa, ki doseže veliko točk (močan napad), vendar tudi dovoli drugi ekipi doseči veliko točk (šibka obramba).
Če želite vnaprej ugotoviti, katere ekipe bodo zmagale, si lahko ogledate standardne odklone različnih "statistik" ekip. Številke, ki se razlikujejo od pričakovanih, se lahko ujemajo s prednostmi in slabostmi, da se pokaže, kateri razlogi so lahko najpomembnejši pri ugotavljanju, katera ekipa bo zmagala.
Na dirkah se meri čas, ki ga voznik porabi za dokončanje vsakega kroga okoli steze. Voznik z majhnim standardnim odklonom časa kroga je bolj dosleden kot voznik z večjim standardnim odklonom. Te informacije lahko uporabimo za lažje razumevanje, kako lahko voznik skrajša čas, potreben za dokončanje kroga.
Denar
V denarju lahko standardni odklon pomeni tveganje, da se bo cena zvišala ali znižala (delnice, obveznice, nepremičnine itd.). Pomeni lahko tudi tveganje, da se bo skupina cen zvišala ali znižala (aktivno upravljani vzajemni skladi, indeksni vzajemni skladi ali skladi ETF). Tveganje je eden od razlogov za sprejemanje odločitev o tem, kaj kupiti. Tveganje je število, s katerim lahko ljudje ugotovijo, koliko denarja lahko zaslužijo ali izgubijo. Ko je tveganje večje, je lahko donosnost naložbe večja od pričakovane ("plus" standardni odklon). Vendar pa lahko naložba tudi izgubi več denarja, kot je bilo pričakovano ("minus" standardni odklon).
Na primer, oseba je morala izbrati med dvema delnicama. Delnica A je imela v zadnjih 20 letih povprečni donos 10 odstotkov s standardnim odklonom 20 odstotnih točk. Delnica B je imela v zadnjih 20 letih povprečno donosnost 12 odstotkov, vendar večji standardni odklon, in sicer 30 odstotnih točk. Če oseba razmisli o tveganju, se lahko odloči, da je delnica A varnejša izbira. Čeprav morda ne bo zaslužila toliko denarja, ga verjetno tudi ne bo veliko izgubila. Oseba bo morda menila, da 2 odstotni točki višje povprečje delnice B ni vredno dodatnih 10 pp standardnega odklona (večje tveganje ali negotovost pričakovanega donosa).
Pravila za normalno porazdeljena števila
Večina matematičnih enačb za standardni odklon predpostavlja, da so števila normalno porazdeljena. To pomeni, da so števila na obeh straneh povprečne vrednosti razporejena na določen način. Normalna porazdelitev se imenuje tudi Gaussova porazdelitev, ker jo je odkril Carl Friedrich Gauss. Pogosto jo imenujemo tudi krivulja zvona, ker se števila razporedijo tako, da imajo na grafu obliko zvona.
Številke niso normalno porazdeljene, če so razvrščene na eni ali drugi strani povprečne vrednosti. Številke so lahko porazdeljene in so še vedno normalno porazdeljene. Standardni odklon pove, kako zelo so števila porazdeljena.

Temno modra barva je manj kot en standardni odklon od povprečja. Pri normalni porazdelitvi to vključuje 68,27 odstotka številk, dva standardna odklona od povprečja (srednje in temno modra) vključujeta 95,45 odstotka, trije standardni odkloni (svetlo, srednje in temno modra) vključujejo 99,73 odstotka, štirje standardni odkloni pa 99,994 odstotka.
Razmerje med povprečjem (sredino) in standardnim odklonom
Povprečje (povprečje) in standardni odklon niza podatkov se običajno zapišeta skupaj. Tako lahko oseba razume, kakšno je povprečno število in kako močno so razpršena druga števila v skupini.
Način porazdelitve skupine številk lahko podamo tudi s koeficientom variacije, ki je standardni odklon, deljen s povprečjem. To je brezrazsežno število. Koeficient variacije se pogosto pomnoži s 100 % in zapiše kot odstotek.
Zgodovina
Izraz standardni odklon je prvič pisno uporabil Karl Pearson leta 1894, potem ko ga je uporabil na predavanjih. Z njim je nadomestil prejšnja imena za isto idejo: Gauss je na primer uporabljal srednjo napako.
Sorodne strani
- Natančnost in natančnost
- Velikost vzorca
Vprašanja in odgovori
V: Kaj je standardni odklon?
O: Standardni odklon je število, ki pove, kako so meritve v skupini oddaljene od povprečja (povprečja ali pričakovane vrednosti).
V: Kaj pomeni majhen standardni odklon?
O: Majhen standardni odklon pomeni, da je večina številk blizu povprečja.
V: Kaj pomeni visok standardni odklon?
O: Visok standardni odklon pomeni, da so številke bolj razpršene.
V: Kako se standardni odklon uporablja v denarju?
O: V denarju standardni odklon zasluženih obresti kaže, kako zelo se lahko zaslužene obresti ene osebe razlikujejo od povprečja.
V: Kdaj lahko merimo samo del skupine?
O: Velikokrat je mogoče izmeriti le vzorec ali del skupine.
V: Kako je predstavljen standardni odklon celotne skupine?
O: Standardni odklon celotne skupine je predstavljen z grško črko َ {\displaystyle \sigma } .
V: Kako je predstavljen standardni odklon vzorca?
O: Standardni odklon vzorca je predstavljen s {\displaystyle s} .
Iskati



