Lavinski učinek v kriptografiji — pomen za blokovne šifre in funkcije hash

Razumevanje lavinskega učinka v kriptografiji: zakaj je ključen za varnost blokovnih šifer in funkcij hash ter kako vpliva na naključnost in odpornost proti kriptoanalizi.

Avtor: Leandro Alegsa Datum ustvarjanja: 11. oktober 2021 Zadnja posodobitev: 22. september 2025

Učinek plazu je temeljna lastnost algoritmov za blokovne šifre in kriptografske funkcije hash. Pogosto je zaželena v kriptografiji, ker zagotavlja, da se majhna sprememba vhoda izrazi kot velika in nerazpoznavna sprememba izhoda. Na praktični ravni učinek pomeni, da mora že najmanjša sprememba v vhodnih podatkih — npr. en bit v odprtem besedilu ali v ključu — povzročiti, da se velik delež (približno polovica) bitov izhodnega bloka spremeni.

Kaj učinek plazu pomeni v praksi

Pri dobrih blokovnih šifrah to pomeni: majhna sprememba ključa ali odprtega besedila mora povzročiti močno spremembo šifriranega besedila. Če se algoritem izvaja z več iteracijami, se majhne spremembe hitro razširijo in sčasoma vplivajo na vsak bit izhoda, torej vsak bit rezultata postane odvisen od vsakega bita vhoda. Takšno širjenje informacij se pogosto imenuje tudi diffuzija (po Shannonu) in je dopolnjeno z zmedo (confusion), ki skrbi za kompleksno odvisnost med ključem in izhodom.

Zgodovina in formalne opredelitve

Izraz učinek plazu je prvi uporabil Horst Feistel (Feistel 1973). Kasneje je koncept povezan in formaliziran z idejami, kot je Shannonova lastnost zmede. V teoriji so bile uvedene tudi natančnejše kriterije, kot so Strict Avalanche Criterion (SAC) in Bit Independence Criterion (BIC), ki merita, kako posamezna sprememba bita vhoda vpliva na porazdelitev izhodnih bitov in medsebojne odvisnosti izhodnih bitov.

Zakaj je učinek plazu pomemben

Če blokovna šifra ali kriptografska funkcija hash v veliki meri ne izpolnjuje lavinskega učinka, potem ima slabo naključnost. Tako lahko kriptoanalitik naredi napovedi o vhodu, če mu je na voljo samo izhod. To lahko zadošča za delno ali popolno razbitje (razbitje) algoritma. Slaba diffuzija lahko olajša napade, kot so diferenčna kriptoanaliza, linearna kriptoanaliza ali druge statistične metode, ki iščejo pristranskosti v izhodu.

Kako doseči dober učinek plazu

Pri oblikovanju močne šifre ali kriptografske funkcije hash je eden glavnih ciljev ustvariti dober lavinski učinek. Načini in gradniki, ki se pogosto uporabljajo:

več krogov (rounds) z izmenjavo nenelinearnih in linearnih komponent,
uporaba S‑polj (S-boxov) za nenelinearnost,
permutacije in matrične operacije za difuzijo (npr. mieszanje v AES),
kombiniranje z XOR, rotacijami in zamenjavami,
uporaba strukture produktnih šifer kot so substitution–permutation networks ali Feistel mreže.

Matematično se pri tem pogosto uporablja analogija z učinkom metulja: majhen lokalni vpliv se skozi iteracije razširi po celotnem stanju. Zato ima večina blokovnih šifer zasnovo, ki združuje zmedo in difuzijo, medtem ko imajo funkcije hash običajno večje podatkovne bloke in več stopenj mešanja, da dosežejo močan učinek plazu po vnosu celo kratke spremembe v sporočilo.

Merjenje in testi

Pri praktičnem preverjanju se pogosto išče, ali sprememba enega bita vhoda povprečno spremeni približno 50 % bitov izhoda. Testiranje vključuje:

empirične teste spreminjanja posameznih bitov in merjenje povprečne stopnje zamenjave izhodnih bitov,
analizo SAC in BIC,
statistične teste za odkrivanje pristranskosti ali korelacij med vhodi in izhodi.

Posledice šibkega lavinskega učinka

Če algoritem ne zagotavlja zadostne razpršitve sprememb, so posledice resne: napadalec lahko izkorišča pristranskosti za rekonstruiranje ključa ali dela vhoda, zmanjša kompleksnost napadov ali celo povzroči popolno razbitje. Prav zato je testiranje učinka plazu standardni del vrednotenja novih šifrirnih metod in funkcij hash.

Primeri in praksa

Uspešne sodobne šifre (npr. AES) in dobro zasnovane hash funkcije običajno pokažejo močan, hitro nastopajoč učinek plazu že po nekaj krogih. Oblikovalci morajo pri tem uravnotežiti varnost in učinkovitost: več krogov običajno pomeni boljši učinek plazu, vendar tudi večjo računsko zahtevnost.

Skupaj: učinek plazu je ključna lastnost za varnost blokovnih šifer in hash funkcij. Dobro razumljena in preverjena implementacija tega učinka močno zmanjša možnost uspešnih kriptoanalitičnih napadov in je zato stalna skrb pri načrtovanju kriptografskih gradnikov.

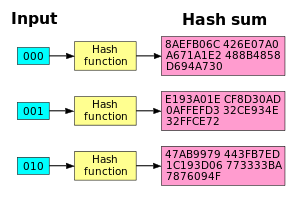
Funkcija SHA1 ima dober lavinski učinek. Ko se spremeni en sam bit, se vsota hasha popolnoma spremeni.

Ime

Izvor imena so zemeljski plazovi. Majhna skala lahko pade skupaj s snegom in ustvari uničujoč zemeljski plaz. Skala je bila majhna, vendar je lahko povzročila veliko uničenja. To je enako kot pri tem učinku. Majhna sprememba na vhodu (skala) naj bi spremenila izhod (pokrajino).

Strogo merilo za plazove

Merilo strogega plazu (SAC; "merilo močnega plazu") je lastnost logičnih funkcij. Pomembno je za kriptografijo. Izpolnjeno je, če se vsi izhodni biti spremenijo s 50-odstotno verjetnostjo, če se spremeni en sam vhodni bit.

SAC je bil zgrajen na konceptih popolnosti evolucije in plazovitosti. Uvedla sta ga Webster in Tavares leta 1985. Danes je zahteva za vsak sodoben kriptografski sistem. Izpolnili so jo npr. vsi finalisti tekmovanja AES.

Merilo neodvisnosti bitov

Merilo neodvisnosti bita (BIC; merilo, neodvisno od bita) je merilo. To pomeni: Ko se en vhodni bit spremeni (invertira), se morata dva izhodna bita spremeniti neodvisno drug od drugega. To velja za vse bite.

Ne bi bilo npr. zadovoljivo, če bi se en izhodni bit spremenil le, če se spremeni tudi drugi izhodni bit. Morda se spremenijo samo zato, ker se je spremenila vhodna bit. V nasprotnem primeru bi bile izhodne bite odvisne druga od druge.

Sorodne strani

Zmešnjava in razpršitev

Vprašanja in odgovori

V: Kaj je učinek plazu?

O: Učinek plazu (znan tudi kot "učinek plazu") je lastnost blokovnih šifer in algoritmov kriptografskih hash funkcij, ki pravi, da mora majhna sprememba v ključu ali odprtem besedilu povzročiti močno spremembo v šifriranem besedilu.

V: Kdo je prvi uporabil izraz "lavinski učinek"?

O: Izraz lavinski učinek je leta 1973 prvi uporabil Horst Feistel.

V: Kako je povezan s Shannonovo lastnostjo zmede?

O: Pojem lavinskega učinka je bil identificiran s Shannonovo lastnostjo zmede, ki pravi, da če blokovna šifra ali kriptografska hash funkcija ne izpolnjuje te stopnje v znatni meri, potem ima slabo naključnost in jo je mogoče delno ali v celoti zlomiti (razbiti).

V: Kateri so nekateri cilji načrtovanja pri ustvarjanju močnih šifer?

O: Ko ljudje ustvarjajo močne šifre, poskušajo vanje vgraditi dober lavinski učinek z uporabo matematičnih načel, kot je učinek metulja. Zato je večina blokovnih šifer produktnih šifer in zato imajo hash funkcije velike podatkovne bloke.

V: Kaj se zgodi, če algoritem ne izpolnjuje lavinskega učinka?

O: Če algoritem v veliki meri ne izpolnjuje lavinskega učinka, ima slabo naključnost in ga lahko kriptoanalitiki delno ali v celoti razbijejo (zlomijo), če lahko na podlagi danih izhodnih podatkov napovedo vhodne podatke.

V: Zakaj večina blokovnih šifer uporablja produktne šifre?

O: Večina blokovnih šifer uporablja produktne šifre, ker vanje z uporabo matematičnih načel, kot je učinek metulja, pomagajo vgraditi dobre učinke avalance.

V: Zakaj imajo hash funkcije velike podatkovne bloke?

O: Šifrirne funkcije imajo velike podatkovne bloke, ker to pomaga ustvariti dobre učinke avalance z uporabo matematičnih načel, kot je učinek metulja.