Gostota verjetnosti
Funkcija gostote verjetnosti je funkcija, ki jo lahko definiramo za katero koli zvezno porazdelitev verjetnosti. Integral funkcije gostote verjetnosti na intervalu [ a , b ] {\displaystyle [a,b]} ![{\displaystyle [a,b]}](https://www.alegsaonline.com/image/9c4b788fc5c637e26ee98b45f89a5c08c85f7935.svg)
daje verjetnost, da je dana naključna spremenljivka z dano gostoto v navedenem intervalu.
Funkcija gostote verjetnosti je potrebna za delo z zveznimi porazdelitvami. Če vržeš kocko, dobiš številke od 1 do 6 z verjetnostjo 1 6 {\displaystyle {\tfrac {1}{6}}} 
, vendar to ni zvezna funkcija, saj so možna samo števila od 1 do 6. Nasprotno pa dve osebi ne bosta enako visoki ali enako težki. S funkcijo gostote verjetnosti je mogoče določiti verjetnost za ljudi, ki merijo med 180 in 181 centimetri ali med 80 in 81 kilogrami, čeprav je med tema dvema mejama neskončno veliko vrednosti.
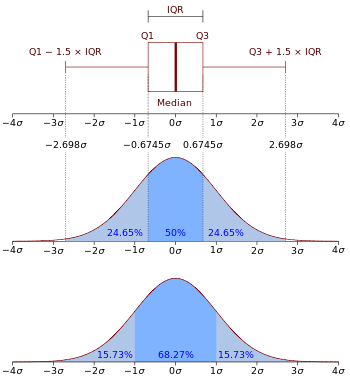
Diagram in funkcija gostote verjetnosti normalne porazdelitve N(0, σ2) .
Vprašanja in odgovori
V: Kaj je funkcija gostote verjetnosti?
O: Funkcija gostote verjetnosti je funkcija, ki označuje vsako zvezno porazdelitev verjetnosti.
V: Kako zapišemo funkcijo gostote verjetnosti naključne spremenljivke X?
O: Funkcija gostote verjetnosti X je včasih zapisana kot f_X(x).
V: Kaj predstavlja integral funkcije gostote verjetnosti?
O: Integral funkcije gostote verjetnosti predstavlja verjetnost, da je dana naključna spremenljivka z dano gostoto vsebovana v predvidenem intervalu.
V: Ali je funkcija gostote verjetnosti vedno nenegativna na celotnem območju?
O: Da, po definiciji je funkcija gostote verjetnosti nenegativna na celotnem območju.
V: Ali je vsota integracije na intervalu enaka 1?
O: Da, integracija na intervalu sešteje do 1.
V: Katero vrsto porazdelitve opisuje funkcija gostote verjetnosti?
O: Funkcija gostote verjetnosti opisuje vsako zvezno verjetnostno porazdelitev.
