Fourierova vrsta
Joseph Fourier je dejal, da je mogoče s sinusnimi valovi aproksimirati drugo funkcijo. To je serija v matematičnem smislu. To teorijo lahko posplošimo na Fourierovo transformacijo. Matematična analiza teh funkcij se imenuje Fourierova analiza.
Že v 18. stoletju so matematiki, kot so Euler, Lagrange in Bernoulli, uporabljali sinusoide za aproksimacijo in modeliranje drugih funkcij. Ko je Fourier leta 1822 objavil delo o vročini, je dejal, da takšni približki obstajajo za vsako takšno funkcijo (ki je zvezna na intervalu). Sprva mu ljudje niso verjeli in trajalo je skoraj deset let, da se je pojavil dokaz (za del problema).
Danes se fourierjeve vrste pogosto uporabljajo pri digitalni obdelavi signalov.
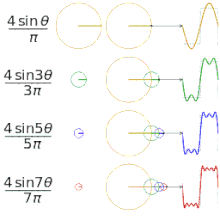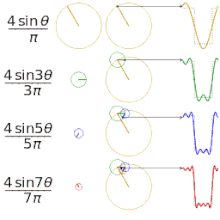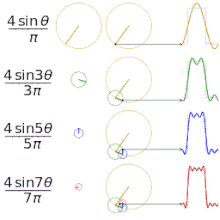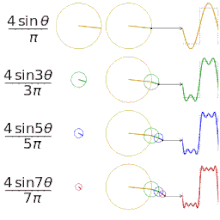
Aproksimacija različnih "kvadratnih" funkcij s fourierjevimi vrstami
Vprašanja in odgovori
V: Kdo je bil Joseph Fourier?
O: Joseph Fourier je bil francoski matematik, ki je predlagal, da se sinusni valovi lahko uporabijo za aproksimacijo druge funkcije.
V: Kaj je Fourierova vrsta?
O: Fourierjeva vrsta je vrsta, ki uporablja sinusne valove za aproksimacijo druge funkcije.
V: Kaj je Fourierova transformacija?
O: Fourierova transformacija je posplošitev teorije, ki uporablja sinusne valove za aproksimacijo druge funkcije.
V: Kaj je Fourierova analiza?
O: Fourierova analiza je matematična analiza funkcij, ki uporabljajo sinusne valove za aproksimacijo druge funkcije.
V: Kdo je v 18. stoletju uporabljal sinusoide za aproksimacijo in modeliranje drugih funkcij?
O: Matematiki, kot so Euler, Lagrange in Bernoulli, so v 18. stoletju uporabljali sinusoide za aproksimacijo in modeliranje drugih funkcij.
V: Kaj je Fourier leta 1822 predlagal v svojem delu o toploti?
O: Fourier je v svojem delu o toploti leta 1822 predlagal, da takšni približki s sinusoidami obstajajo za vsako zvezno funkcijo na danem intervalu.
V: Kakšna je uporaba Fourierovih vrst pri digitalni obdelavi signalov?
O: Fourierjeve vrste se pogosto uporabljajo pri digitalni obdelavi signalov za aproksimacijo in analizo signalov.
