Arhimedova telesa: definicija, lastnosti in zgodovina
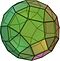
Arhimedovo telo je v geometriji konveksna oblika, sestavljena iz mnogokotnikov. Gre za posebno vrsto uniformnega poliedra, znanega po svojih pravilnih ploskvah in simetriji. To je polieder z naslednjimi lastnostmi:
- Vsaka stran je sestavljena iz pravilnega mnogokotnika.
- Vsi vogali oblike so enaki
- Oblika ni ne platonska trdna snov, ne prizma in ne antiprizma.
Razlaga lastnosti
Pomembno je poudariti, da so Arhimedova telesa uniformni poliedri: njihove ploskve so pravilni mnogokotniki (lahko več vrst), robovi so enake dolžine in skupine simetrij omogočajo, da je okoli vsakega vozlišča enaka razporeditev ploskev. Iz tega sledi, da so vsi vogali (vozlišča) enaki iz perspektive simetrije (t. i. vertex‑transitive). Vendar pa se ploskve lahko razlikujejo po obliki (npr. trikotniki, kvadrati, peterokotniki hkrati).
Število in različice
Običajno se prizna 13 Arhimedovih teles, če štejemo oblike, ki so med seboj zrcalne (levoročne in desnoroke) kot isto obliko. Če pa takšne zrcalne pare obravnavamo kot različne (ker jih z vrtenjem ni mogoče uskladiti), je skupno število 15. Dve od teh oblik imata pravzaprav dve različici, ki ju ni mogoče uskladiti z vrtenjem — to sta snub‑kocka in snub‑dodekaeder (snub cube in snub dodecahedron), ki se pojavljata v dveh enantiomorfnih (zrcalnih) oblikah.
Zgodovinski pregled
Arhimedova telesa nosijo ime po starogrškem matematiku Arhimedu, ki jih je verjetno prvi opisal v 3. stoletju pr. n. št. Njegovi izvirni spisi o teh telesih so se žal izgubili; v 4. stoletju pa jih je povzel in omenil Pappus iz Aleksandrije. V renesansi so umetniki in matematiki znova odkrili in zelo cenili te čiste oblike zaradi estetskih in simetričnih lastnosti. Johannes Kepler je na začetku 17. stoletja prispeval k razumevanju in izpopolnitvi iskanja uniformnih poliedrov, okoli leta 1620 pa je bila problematika skoraj zaključena — končno, strogo dokazana uvrstitev 13 konveksnih Archimedovih teles pa izhaja iz poznejših matematičnih dokazov.
Konstrukcija in metode
Mnoga Arhimedova telesa lahko dobimo z operacijami nad platonskimi telesi ali med seboj, na primer:
- odrezovanje (truncation) vogalov platonskih teles,
- rektilacija (rectification) — odrezovanje do stika ploskev,
- kantelacija (cantellation) — odrezovanje robov in vogalov,
- snubiranje (snubbing) — vrtenje in premik delov za dosego chiralnih oblik.
Za konstrukcijo Arhimedovega telesa sta pogosto potrebna vsaj dva različna mnogokotnika; to pomeni, da en sam tip pravilnega mnogokotnika (npr. samo kvadrati ali samo trikotniki) ne zadostuje, če želimo dobiti netradicionalno Archimedovo obliko (izjeme so nekatere kombinacije, vendar je splošno pravilo, da gre za kombinacijo različnih pravilnih mnogokotnikov).
Primeri in uporaba
Med bolj znanimi primeri so oblike, ki nastanejo z obrezovanjem platonskih teles — npr. odrezani tetraeder ali odrezani ikozaeder. Najbolj znana praktična uporaba je truncated icosahedron (oblika, ki jo ima klasična nogometna žoga), ki je prav tako struktura molekule fulerena C60. Arhimedova telesa se pojavljajo v arhitekturi, umetnosti, industriji in kemiji zaradi svoje kombinacije estetske simetrije in stabilnosti.
Matematične lastnosti
Za vsa konveksna poliedra velja Eulerjeva zveza V − E + F = 2 (kjer so V vozlišča, E robovi, F ploskve). Pri Arhimedovih telesih je zanimivo tudi zapisovanje konfiguracije vogala v obliki niza števil (npr. (3,4,3,4) pomeni, da se pri vsakem vozlišču izmenjujejo trikotnik in kvadrat). Poleg tega ima vsako Archimedovo telo pripadajočo skupino simetrij, ki določa enakost vseh vogalov.
Zaključek
Arhimedova telesa predstavljajo pomembno skupino v geometriji: so konveksni, uniformni poliedri z več vrstami pravilnih mnogokotnikov na ploskvah in z enakomernimi vozlišči. Čeprav izhajajo iz antičnih opisov, so njihova lastnosti, konstrukcije in uporabe predmet sodobnih raziskav v matematiki, fiziki, kemiji in oblikovanju.
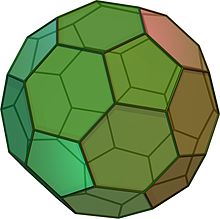
Posekani ikozaeder je videti kot nogometna žoga. Sestavljen je iz 12 enakostraničnih petkotnikov in 20 pravilnih šestkotnikov. Ima 60 vrhov in 90 robov. Je Arhimedovo telo.
Lastnosti
- Arhimedova telesa so sestavljena iz pravilnih mnogokotnikov, zato so vsi robovi enako dolgi.
- Vsa Arhimedova telesa lahko dobimo iz platonskih teles z "rezanjem robov" platonskega telesa.
- Vrsta mnogokotnikov, ki se stikajo na vogalu ("vrh"), je značilna za arhimedovo in platonsko telo.
Povezava s platonskimi telesi
Platonska telesa lahko spremenimo v Arhimedova telesa, če upoštevamo vrsto pravil za njihovo konstrukcijo.
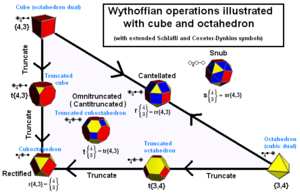
Arhimedova telesa lahko konstruiramo kot položaje generatorjev v kalejdoskopu
Seznam Arhimedovih teles
V nadaljevanju je seznam vseh Arhimedovih teles
| Slika | Ime | Obrazi | Tip | Robovi | Vrhovi |
|
| Posekani tetraeder | 8 | 4 trikotniki 4 šestkotniki | 18 | 12 |
|
| 14 | 8 trikotnikov 6 kvadratov | 24 | 12 | |
|
| Posekana kocka | 14 | 8 trikotnikov 6 osmerokotnikov | 36 | 24 |
|
| Okrašen oktaeder | 14 | 6 kvadratov 8 šestkotnikov | 36 | 24 |
|
| Rombikubokoktaeder | 26 | 8 trikotnikov 18 kvadratov | 48 | 24 |
|
| Obrezani kuboktaeder | 26 | 12 kvadratov 8 šestkotnikov 6 osmerokotnikov | 72 | 48 |
|
| Kocka Snub (2 zrcalni različici) | 38 | 32 trikotnikov 6 kvadratov | 60 | 24 |
|
| Ikozidodekaeder | 32 | 20 trikotnikov 12 peterokotnikov | 60 | 30 |
|
| Okrašen dodekaeder | 32 | 20 trikotnikov 12 dekagonov | 90 | 60 |
|
| Posekani ikozaeder | 32 | 12 peterokotnikov 20 šestkotnikov | 90 | 60 |
|
| Rombikoidodekaeder | 62 | 20 trikotnikov30 kvadratov12 | 120 | 60 |
|
| Posekan ikozidodekaeder | 62 | 30 kvadratov 20 šestkotnikov 12 dekagonov | 180 | 120 |
|
| Snub dodekaeder (2 zrcalni različici) | 92 | 80 trikotnikov 12 peterokotnikov | 150 | 60 |
Vprašanja in odgovori
V: Kaj je Arhimedova trdna snov?
O: Arhimedovo telo je konveksna oblika, sestavljena iz mnogokotnikov, ki ima lastnost, da je vsaka stran pravilen mnogokotnik, da so vsi vogali videti enako in da ni platonsko telo, prizma ali antiprizma.
V: Koliko je Arhimedovih trdnih teles?
O: Odvisno od načina štetja je trinajst ali petnajst Arhimedovih teles.
V: Kdo je odkril Arhimedova telesa?
O: Arhimedova telesa so dobila ime po starogrškem matematiku Arhimedu, ki jih je verjetno odkril v 3. stoletju pred našim štetjem.
V: Kaj je Pappus iz Aleksandrije naredil z Arhimedovimi spisi?
O: Pappus Aleksandrijski je v 4. stoletju povzel Arhimedove spise o Arhimedovih trdnih telesih.
V: Zakaj so umetniki in matematiki v renesansi ponovno odkrili Arhimedova telesa?
O: V renesansi so umetniki in matematiki cenili čiste oblike, Arhimedova telesa pa so veljala za čiste oblike.
V: Kdaj je Johannes Kepler končal iskanje vseh Arhimedovih teles?
O: Johannes Kepler je iskanje vseh Arhimedovih teles verjetno končal okoli leta 1620.
V: Kaj je potrebno za sestavo Arhimedove trdne snovi?
O: Za konstrukcijo Arhimedovega telesa sta potrebna vsaj dva različna mnogokotnika.
