Svetlobna ura: pojasnilo časovne dilatacije v posebni teoriji relativnosti

Svetlobna ura je preprost in pregleden način za pojasnitev osnovne lastnosti posebne teorije relativnosti. Ura deluje tako, da se svetlobni blisk odbije od oddaljenega zrcala in se ob povratku sproži naslednji blisk; medtem se šteje, koliko bliskov je minilo. Enostavno je pokazati, da bi opazovalci na Zemlji, ki bi gledali vesoljsko ladjo, ki se giblje hitro nad njimi, videli, da ta ura tiktaka počasneje. Ta učinek se imenuje dilatacijačasa.

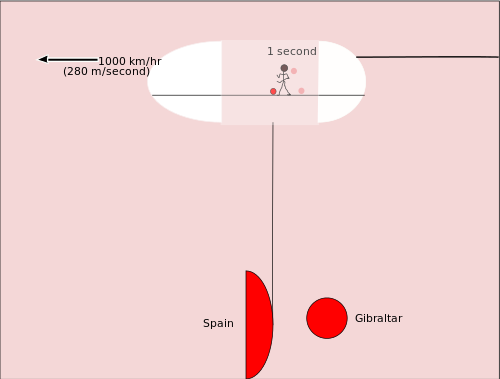
Preden preučimo svetlobno uro, si oglejmo še en primer relativnega gibanja. Predstavljajte si košarkarja, ki driblja v prtljažnem prostoru reaktivnega letala. Košarkar v svoji sobi opravi en dribling v približno eni sekundi; drugi potniki v letalu vidijo, da se košarkar premakne le meter ali dva v svojem prostoru. Vendar pa glede na Zemljo (zaradi hitrosti letala) lopta med prvim in drugim odbojem dejansko prepotuje večjo razdaljo — recimo 280 metrov — ker se letalo medtem premakne. To ponazarja, da so poti in časi relativni glede na različno gibanje opazovalcev.

Opis svetlobne ure

Za osnovni model naredimo naslednje: postavimo izvor svetlobe na dno dolgega droga, nad njim je ogledalo in ob dnu detektor, ki šteje prejet svetlobni utrip in sproži naslednjega. Ko detektor zazna utrip, poveča števec in pošlje nov utrip navzgor. Če drog meri pol kilometra, bo vsako "tiktakanje" svetlobe prepotovalo razdaljo 1 km (gor in nazaj). Ker je hitrost svetlobe konstanta c (približno 300.000 km/s), je čas enega tiktaka pri mirujoči uri:

d = c t,

kjer je d = 1 km, torej

t = d / c = 1 km / 300 000 km/s ≈ 1/300 000 s ≈ 0,00000333 s.

Tako je to čas intervala, ki ga izmeri ura, ko je v mirovanju glede na opazovalca (npr. ura postavljena na Severnem tečaju).

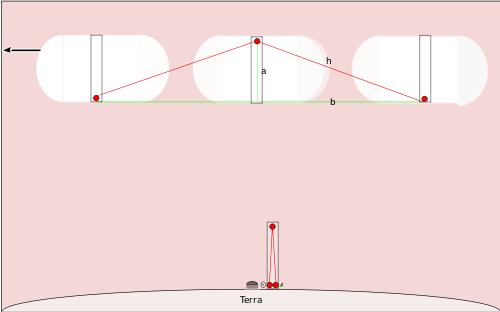
Svetlobna ura na premikajoči se ladji

Zdaj si predstavljamo popolnoma enako uro, vendar nameščeno na vesoljski ladji, ki se premika vodoravno z hitrostjo r (v klasični notaciji običajno v). Za opazovalca na Zemlji svetloba med vzponom in padcem ne potuje več navpično, temveč po poševni poti, ker se ladja medtem premika. Če naj bo pol dolžine droga na ladji a, potem v ladijinem lastnem (počivajočem) sistemu traja en "tik" čas t = 2a / c (gor in nazaj). Za opazovalca na Zemlji pa je dolžina poti svetlobe večja — vsakič potuje po hipotenuzi trikotnika, kjer je vodoravna premik v času vzpona enak (r t'/2), če je t' čas, ki ga Zemljin opazovalec pripiše enemu tiktaku ladijske ure.

Če označimo pol poti do ogledala kot višino h, s Pitagorovim izrekom velja:

h = √(a² + (r t' / 2)²)

Celotna pot svetlobe (gor in nazaj) pa je d = 2 h. Ker je hitrost svetlobe c enaka za vse opazovalce, lahko zapišemo tudi:

c t' = d = 2 √(a² + (r t' / 2)²)

Izpeljava enačbe dilatacije časa

Kvadriramo obe strani in uredimo izraz:

c² t'² = 4 a² + r² t'²

Premaknemo člen z r² t'² na levo:

t'² (c² − r²) = 4 a²

Od tod:

t' = 2 a / √(c² − r²) = (2 a / c) · 1 / √(1 − r² / c²)

Ker je čas v mirovanju (čas med tiktaki ure v jej lastnem sistemu) t = 2 a / c, dobimo končno razmerje:

t' = t / √(1 − r² / c²)

Faktor 1 / √(1 − r² / c²) je znan kot Lorentzov faktor ali γ (gamma). Za hitrost r = c/2 (pol hitrosti svetlobe) je γ = 1 / √(1 − 1/4) = 1 / √(3/4) ≈ 1,1547, kar pomeni, da bi opazovalci na Zemlji videli, da en tiktak ladijske ure traja približno 1,1547–krat dlje kot isti tiktak pri mirujoči uri. Če je t = 1 sekunda v lastnem sistemu ure, opazovalec v drugi referenčni ravnini zabeleži t' ≈ 1,1547 s.

Pomen in posledice

• Dilatacija časa pomeni, da se ure, ki se gibljejo hitro glede na opazovalca, "počasi" tiktakajo v tem opazovalčevem merilu. To ni napaka ure, temveč posledica geometrije prostora in časa v posebni relativnosti.
• Učinek je simetričen: v sistemu, ki miruje z uro, je ura normalna in to opazijo potniki; opazovalci v drugem sistemu vidijo uro kot upočasnjeno. Relativnost simultanosti določi, kako se primerjajo dogodki v različnih sistemih.
• Eksperimentalni dokazi: dilatacija časa je bila potrjena z meritvami časa življenja hitrih delcev v sprejemnikih, z atomsko-urami na letalih in je ključna za pravilno delovanje GPS — satelitske ure morajo upoštevati relativistične popravke.
• Praktičen primer: muoni, nastali v atmosferi, zaradi velike hitrosti dosegajo zemeljsko površje pogosteje, kot bi pričakovali iz njihove mirovanje življenjske dobe — to je neposreden dokaz dilatacije časa.

Kratek povzetek

Svetlobna ura ponuja preprosto, geometrijsko razlago dilatacije časa: ko se ura giblje, svetloba pri doseganju ogledala in vrnitvi opravi daljšo pot glede na zemeljske opazovalce, zato ti merijo daljši čas med dvema utripoma. Matematično to pripelje do relacije t' = t / √(1 − r² / c²), kjer je t čas med tiktaki v lastnem (mirujočem) sistemu ure, t' pa čas, ki ga isti interval zabeleži opazovalec v sistemu, kjer se ura giblje s hitrostjo r.

Za interaktivne simulacije in poskuse z različnimi hitrostmi obiščite: http://www.1728.org/reltivty.htm

Vprašanja in odgovori

V: Kaj je svetlobna ura?

V: Kaj je časovna dilatacija?

V: Kako lahko izračunamo, za koliko se upočasni čas na vesoljski ladji?

V: Kako deluje svetlobna ura?

V: Kakšno enačbo potrebujemo za ta izračun?

V: Kaj ima Pitagorov teorem opraviti s tem izračunom?

Išči po črki