Paralaksa: definicija in uporaba pri merjenju razdalj v astronomiji
Paralaksa: definicija in uporaba pri merjenju razdalj v astronomiji — kako paralaksa deluje, meritve Hipparcos in Gaia ter pomen za natančno določanje razdalj.
Paralaksa je zaznana sprememba položaja predmeta, ki ga vidimo z dveh različnih krajev. V astronomiji ta pojav uporabljamo kot osnovno in neposredno metodo za določanje razdalj do bližnjih nebesnih teles.
Kako deluje paralaksa
Pri astronomski (letni) paralaksi opazujemo isto zvezdo iz različnih položajev Zemlje na njeni orbiti okoli Sonce, običajno v razmaku šestih mesecev. Zaradi spremembe pozicije opazovalca se zdi, da se položaj zvezde na ozadju bolj oddaljenih teles rahlo spremeni. Kot, ki ga merimo, je običajno polovica tega skupnega premika — to je t. i. paraksni kot.
Merjenje in osnovne enačbe
Geometrija temelji na trikotniku, katerega osnovnica je znana (polmer Zemljine orbite, torej 1 astronomična enota — 1 AU) in ogli so opazovani. Z merjenjem paraksnega kota p lahko izračunamo razdaljo d.
- Za majhne kote velja približek iz majhnega kota: d ≈ 1 AU / p (v radianih).
- V astronomiji se kot običajno meri v loknih sekundah in razdalje v parsekih; definicija parseka:
- d (v parsekih) = 1 / p (v loknih sekundah)
- Parsek je torej razdalja, pri kateri 1 AU zasede kot 1".
Vrste paralakse in primeri
- Letna (astronomska) paralaksa: uporablja se za zvezde; osnovnica je 2 AU (celotni premik med opažanji v nasprotnih točkah orbite), paraksni kot pa se navadno definira kot polovica tega premika.
- Diurnalna paralaksa: nastane zaradi premika opazovalca pri vrtenju Zemlje; pomembna je pri merjenjih bližnjih teles, npr. Lune, kjer je lahko merljiva in delno uporablena za določanje oddaljenosti.
- Solarna paralaksa: kot, ki ga 1 AU zasede z vidika površine Zemlje pri opazovanju Sonca — zgodovinsko pomembna za določanje velikosti Osončja.
Omejitve metode in sodobne izboljšave
Glavna omejitev metode je zelo majhen kot pri velikih razdaljah: če je zvezda zelo oddaljena, je paraksni kot manjši od meritvene natančnosti instrumenta. Pred sateliti, kot je bil Hipparcos, so bile natančne meritve paralakse omejene na relativno bližnje zvezde. Hipparcos je med letoma 1989 in 1993 opravil meritve za več kot 100.000 bližnjih zvezd, znatno izboljšal natančnost in razširil območje uporabnosti metode.
Posnetek in nadaljnje misije so še bolj povečale razpon in natančnost: satelit Gaia (vesoljsko plovilo) je v naslednjih izdajah meritev zagotovil paralse za več sto milijonov do prek milijarde zvezd z veliko večjo natančnostjo (mikro- do milisekundne ravni za svetlejše zvezde), kar omogoča določanje razdalj do zvezd na tisoče parsekov.
Čeprav obstajajo drugi načini za oceno razdalj (npr. standardne sveče, spektroskopske metode, cepheidne spremenljivke), nobena ni tako neposredna in brez modelnih predpostavk kot paralaksa. Zaradi tega je paralaksa temelj za lestev kozmičnih razdalj s tehnikami za izračun večjih razdalj.
Zgodovinski in praktični vidiki
Prvo neposredno meritev zvezdne paralakse je leta 1838 izvedel Friedrich Bessel za zvezdo 61 Cygni, kar je bilo ključno za dokaz, da so zvezde res izjemno oddaljene. Danes natančnost meritev in velik obseg podatkov iz misij, kot sta Hipparcos in Gaia, omogoča natančno kartiranje gibanja in porazdelitve zvezd v naši Galaksiji.
Paralaksa v biologiji: stereopsis
Paralaksa ni le astronomija — ime povezanega pojava najdemo tudi pri živalih: številne živali, tudi ljudje, imajo dve očesi, ki sta nekoliko razmaknjeni. Razlika v vidnem kotu obeh oči omogoča zaznavanje globine, kar imenujemo stereopsis. Ker sta očesi na različnih mestih na glavi, je to naravna osnova za samodejno zaznavanje razdalje in tridimenzionalne percepcije, kar dojemamo kot običajen tridimenzionalni prizor.
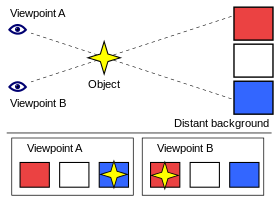
Primer paralakse predmeta na oddaljenem ozadju zaradi spremembe lokacije. Ob pogledu z "gledišča A" se zdi, da je predmet pred modrim kvadratom. Ko pogled spremenimo na "točko B", se zdi, da se je predmet premaknil pred rdeči kvadrat.
Vprašanja in odgovori
V: Kaj je paralaksa?
O: Paralaksa je zaznana sprememba položaja predmeta, ki ga vidimo z dveh različnih krajev. Meri se s kotom med dvema opazovalnima črtama in se lahko uporablja za določanje razdalj.
V: Kako se paralaksa uporablja v astronomiji?
O: V astronomiji je letna paralaksa edini neposredni način za merjenje razdalje do zvezd zunaj sončnega sistema. Astronomi uporabljajo načelo paralakse za merjenje razdalj do nebesnih teles, vključno z Luno, Soncem in zvezdami zunaj Osončja.
V: Kako izračunamo razdaljo s pomočjo paralakse?
O: Astronomske meritve položaja se izvajajo v različnih letnih časih. Ker je Zemljina orbita natančno znana, lahko izračunamo razdaljo od položaja 1 do položaja 2. Natančno se lahko izmeri kot od obzorja do objekta, s čimer dobimo trikotnik, katerega osnovna črta in koti so natančno znani. Iz tega trikotnika lahko s trigonometrijo izračunamo razdalje, izražene v parsekih.
V: Ali obstajajo kakšne omejitve pri uporabi paralakse za merjenje oddaljenih objektov?
O: Da, ne uspe pri objektih, ki so tako oddaljeni, da je Zemljina orbita premajhna za dovolj velik kot paralakse za natančne meritve - približno 100 svetlobnih let ali več. Izumljene so bile tudi druge metode, vendar nobena ni tako natančna kot paralaksa za relativno bližnje objekte.
V: Kateri satelit je bil v letih 1989-1993 uporabljen za merjenje bližnjih zvezd?
O: V tem obdobju je satelit Hipparcos opravil meritve več kot 100 000 bližnjih zvezd.
V: Katero vesoljsko plovilo bo opravilo podobne meritve kot Hipparcos? O: Gaia (vesoljsko plovilo) bo opravilo podobne meritve približno milijarde zvezd.
Iskati