Evklidov peti postulat (vzporedni postulat): definicija in pomen
Evklidov peti postulat (vzporedni postulat): jasna definicija, zgodovina in pomen v geometriji — razumite vzporednice ter razliko med evklidsko in neevklidsko geometrijo.
V geometriji je vzporedni postulat eden od aksiomov evklidske geometrije. Včasih se imenuje tudi Evklidov peti postulat, ker je peti postulat v Evklidovih Elementih.
Postulat pravi, da:
Če odsek presekate z dvema premicama in sta notranja kota, ki ju tvorita premici, manjša od 180°, se bosta premici sčasoma srečali, če ju boste dovolj podaljšali.
Področje geometrije, ki upošteva vse Evklidove aksiome, se imenuje evklidska geometrija. Geometrije, ki ne upoštevajo vseh Evklidovih aksiomov, se imenujejo neevklidska geometrija.
Kaj pomeni postulat v praksi?
Vzporedni postulat določa, kako se obnašajo premice v ravnini glede na pojme, kot so "vzporednost" in "zravennje". V enostavnih besedah pravi, da se v ravnini ne moreta nahajati dve premici, ki bi bili hkrati različni in bi se nikoli ne sekali, če velja določena geometrijska konfiguracija kot jo Evklid opisuje.
Najpogostejša sodobna različica, ki se pogosto uporablja v učbenikih, je Playfairov aksiom:
- Pri dani premici in točki izven te premice obstaja natanko ena premica, ki je vzporedna dani premici.
Izreki, ekvivalentni vzporednemu postulatu
Vzporedni postulat je matematično ekvivalenten številnim drugim trditvam; to pomeni, da če sprejmete katerega od teh izrekov kot aksiom, lahko izpeljete preostale. Nekateri pomembni primeri:
- Vsota notranjih kotov v trikotniku je enaka 180°.
- Obstoj pravokotnikov: obstaja poljubno velik pravokotnik.
- Če sta dve premici vzporedni tretji premici, sta med seboj vzporedni.
- Playfairov aksiom (kot zgoraj).
Zgodovina in pomembni prispevki
Evklid je vzporedni postulat zapisal kot enega od svojih aksiomov v delu Elementi. Že dolgo so matematikom postajale očitne druge aksiome, medtem ko je peti izpadal manj "naraven" in so mnogi poskušali postulat izpeljati iz preostalih Evklidovih aksiomov.
V 18. in 19. stoletju so številni matematikom (npr. Girolamo Saccheri, Johann Heinrich Lambert) preizkušali dokaze napačnosti ali izpeljave petega postulata. Sčasoma so Neodvisnost postulata pokazali N. I. Lobachevsky, János Bolyai in Eugenio Beltrami z razvojem konzistentnih neevklidskih geometrij v začetku 19. stoletja. Karl Friedrich Gauss je prav tako razmišljal o tem, vendar večino svojih idej ni objavil.
Neodvisnost in neevklidske geometrije
Pomembna posledica teh zgodovinskih raziskav je bila spoznanje, da vzporedni postulat ni posledica preostalih Evklidovih aksiomov — torej je neodvisen. To je omogočilo vznik dveh glavnih vrst neevklidskih geometrij:
- Hiperbolična geometrija (Lobachevsky, Bolyai): skozi točko zunaj premice poteka več kot ena premica, ki so vzporedne izbrani premici (lahko rečemo: obstaja neskončno množico "paralel").
- Eliptična ali sferična geometrija (Riemannove ideje): ne obstajajo vzporednice, saj se vse "premice" (veliki krogi) na sferi sekajo.
Posledice za geometrijo in prakso
Mnogi standardni izreki iz osnovne geometrije so odvisni od vzporednega postulata. Med njimi so:
- Sum kotov v trikotniku = 180° (evklidsko). V hiperbolični geometriji je manjša od 180°, v eliptični večja od 180°.
- Lastnosti podobnosti trikotnikov in proporcionalnost stranic v podobnih trikotnikih.
- Obstoj in lastnosti pravokotnikov ter evklidski razvoj mer in geometrije v vsakodnevnih aplikacijah (zemljepisna kartografija, inženirstvo itd.).
Kaj to pomeni za učenje geometrije?
Razumevanje vloge vzporednega postulata pomaga ločiti, katere geometrijske trditve izhajajo iz "čiste logike" in katere so posledica oblikovanja prostora (Evklidskega ali neevklidskega). V šolski praksi je Playfairova formulacija pogosto najprimernejša za intuitivno učenje pojma vzporednosti, medtem ko je zgodovinski pogled koristen pri razumevanju razvoja matematičnega mišljenja.
Za hitri povzetek: Evklidov peti postulat ureja vedenje premic v ravnini in je temelj, iz katerega izhajajo številne lastnosti klasične (evklidske) geometrije. Njegova neodvisnost od drugih aksiomov je odprla pot do novih geometrijskih teorij in globljega razumevanja prostora.
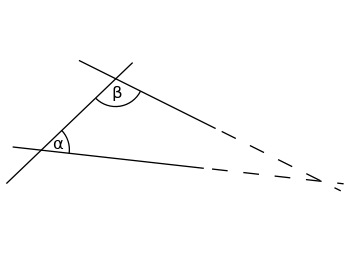
Če je vsota notranjih kotov α (alfa) in β (beta) manjša od 180°, se premici nekje sekata, če sta obe podaljšani do neskončnosti.
Zgodovina
Nekateri matematiki so menili, da je Evklidov peti postulat veliko daljši in bolj zapleten od ostalih štirih postulatov. Mnogi med njimi so menili, da ga je mogoče dokazati na podlagi drugih, preprostejših aksiomov. Nekateri matematiki so razglasili, da so ga dokazali iz preprostejših postulatov, vendar se je izkazalo, da so se vsi zmotili.
Playfairjev aksiom
Druga novejša trditev, znana kot Playfairjev aksiom, je podobna Evklidovemu petemu postulatu. Pravi, da:
Če imamo premico in točko, ki ni na tej premici, lahko skozi to točko narišemo le eno premico, ki se ne bo srečala z drugo premico.
Matematiki so ugotovili, da ta aksiom ni le podoben Evklidovemu petemu postulatu, ampak ima povsem enake posledice. Matematično se oba stavka imenujeta "enakovredna" stavka. Danes matematiki Playfairjev aksiom uporabljajo pogosteje kot prvotni Evklidov vzporedni postulat.
Neevklidska geometrija
Sčasoma so nekateri matematiki poskušali zgraditi nove geometrije brez uporabe aksioma. Ena od vrst neevklidske geometrije se imenuje eliptična geometrija. V eliptični geometriji je vzporedni postulat nadomeščen z aksiomom, ki pravi, da:
Če imamo premico in točko, ki ni na tej premici, ne moremo narisati premice skozi to točko, ki na koncu ne bi prečkala druge premice.
Matematiki so ugotovili, da so lahko, ko so Evklidov peti postulat nadomestili s tem aksiomom, še vedno dokazali številne druge Evklidove trditve. Elipsno geometrijo si lahko predstavljamo tako, da pomislimo na površino globusa. Na globusu se zdi, da so daljnovodne črte na ekvatorju vzporedne, vendar se vse stikajo na polih. Konec 19. stoletja se je pokazalo, da je eliptična geometrija dosledna. To je dokazalo, da Evklidov peti postulat ni neodvisen od drugih postulatov. Po tem so matematiki večinoma prenehali dokazovati peti postulat na podlagi drugih štirih postulatov. Namesto tega so mnogi matematiki začeli preučevati druge geometrije, ki ne sledijo Evklidovemu petemu postulatu.
Drug aksiom, s katerim matematiki včasih nadomestijo Evklidov peti aksiom, pravi:
Če imamo neko premico in točko, ki ne leži na tej premici, lahko skozi to točko narišemo vsaj dve premici, ki na koncu ne prečkata druge premice.
To se imenuje hiperbolična geometrija.
Druga geometrija preprosto odstrani Evklidov peti postulat in ga z ničemer ne nadomesti. To imenujemo nevtralna geometrija ali absolutna geometrija.
Iskati