Znak v matematiki: pomen, vrste in uporaba (pozitivno, negativno, nič)

Znak v matematiki: pomen, vrste in uporaba – jasna razlaga pozitivnega, negativnega in nič s primeri ter pravili za računanje.

V matematiki se beseda znak nanaša na lastnost pozitivnosti ali negativnosti. Vsako realno število (ki ni nič) je pozitivno ali negativno in ima zato znak. Sama ničla je brez znaka ali brez predznaka. Poleg dodajanja znakov realnim številom se beseda znak v matematiki uporablja tudi za označevanje delov matematičnih objektov, ki pomenijo pozitivnost in negativnost. Običajno, če vidimo števila brez znaka, jih obravnavamo kot pozitivna števila.

Beseda znak se včasih uporablja tudi za različne matematične znake, kot so znaki plus in minus ter znak za množenje.

Kaj pomeni "znak" pri številih

Znak števila pove, ali je število pozitivno ali negativno. Pozitivna števila imajo predznak + (pogosto ga izpustimo), negativna pa predznak −. Na primer: +5 ali preprosto 5 je pozitivno, medtem ko je −3 negativno. Nižja posebnost: ničla nima predznaka — ni ne pozitivna ne negativna.

Notacija in simboli

• + pomeni pozitivno ali se uporabi za seštevanje.
• − pomeni negativno ali se uporabi za odštevanje.
• Pri zapisu realnih števil običajno izpuščamo znak +: pišemo 5 namesto +5.
• Funkcija znaka (pogosto zapišemo sgn) pripiše številu vrednosti −1, 0 ali +1 (glej spodaj).

Osnovna pravila za računanje s predznaki

Pri množenju in deljenju veljajo preprosta pravila za predznake:

• + × + = +
• − × − = +
• + × − = −
• Enaka pravila veljajo tudi za deljenje: (−a)/(−b) = a/b, (−a)/b = −(a/b).

Pri seštevanju in odštevanju je odločilen velikostni odnos števil (absolutnih vrednosti):

• Če seštejemo števili z enakim predznakom, se absolutni vrednosti seštejeta in predznak ostane enak.
• Če seštejemo števili z različnima predznakoma, odštejemo manjšo absolutno vrednost od večje in prevladujoči predznak pripišemo rezultatu.
• Odštevanje je enako seštevanju z nasprotnim predznakom: a − b = a + (−b).

Funkcija znaka (sgn)

Funkcija znaka je uporabna za formalno označevanje predznaka števila:

• sgn(x) = +1, če je x > 0
• sgn(x) = 0, če je x = 0
• sgn(x) = −1, če je x < 0

Funkcija znaka se pogosto uporablja pri analizi funkcij, pri reševanju enačb in sistemov ter pri dokazih, ki temeljijo na lastnostih predznakov.

Absolutna vrednost in povezava z znakom

Absolutna vrednost |x| je vedno nenegativna in daje velikost števila brez predznaka. Od števila ga lahko ponovno dobimo z množenjem z njegovim znakom:

x = sgn(x) · |x| (razen za x = 0, kjer sgn(0) = 0).

Posebnosti in razširitve

• Kompleksna števila nimajo urejenega pojma pozitivno/negativno, zato za kompleksna števila govorimo o absolutni vrednosti (modulu) in argumentu, ne pa o predznaku v realnem smislu.
• Računalništvo: obstajajo "signed" (s predznakom) in "unsigned" (brez predznaka) podatkovni tipi. Pri plavajočih pticah (floating point) je možen pojav −0, ki je poseben zapis z negativnim predznakom, a pri primerjavah je −0 običajno enak 0.
• Sprememba predznaka: operator − pred številom spremeni njegov znak: −(−a) = a.
• Diagrami znakov: pri analizi funkcij se pogosto uporabi tabelo ali številčno os, da se prikaže, kje je funkcija pozitivna, negativna ali ničelna (znakovni diagram ali sign chart).

Uporaba v praktičnih primerih

• Reševanje enačb in neenačb: predznaki vplivajo na rešitve (npr. kvadratna funkcija je vedno ≥ 0, linearne funkcije spreminjajo predznak ob ničlah).
• Fizikalne količine: smeri (hitrost, pospešek) pogosto modeliramo z znaki (pozitivno ena smer, negativno nasprotna).
• Finančne aplikacije: dobiček in izguba se običajno predstavljata s pozitivnimi oziroma negativnimi vrednostmi.

Kratek povzetek

• Znak pove, ali je realno število pozitivno ali negativno; ničla nima predznaka.
• Pri množenju in deljenju velja preprosto pravilo: enaka predznaka da pozitiven rezultat, različna da negativnega.
• Funkcija sign(x) je uporabna za formalno določitev predznaka: +1, 0 ali −1.
• V nekaterih področjih (kompleksna števila, računalniški tipi) je interpretacija znaka drugačna ali omejena.

Pomen znakov

Ker ničla ni niti pozitivna niti negativna, se za označevanje znaka neznanega števila včasih uporabljajo naslednje besede:

• Število je pozitivno, če je večje od nič.
• Število je negativno, če je manjše od nič.
• Število je nenegativno, če je večje ali enako nič.
• Število ni pozitivno, če je manjše ali enako nič.

Tako je nenegativno število pozitivno ali nič, nepozitivno število pa je negativno ali nič. Na primer, absolutna vrednost realnega števila je vedno nenegativna, vendar ni nujno pozitivna.

Enaka opredelitev se včasih uporablja za funkcije, ki sprejemajo realne ali celoštevilske vrednosti. Funkcija se na primer imenuje pozitivna, če so vse njene vrednosti pozitivne, ali nenegativna, če so vse njene vrednosti nenegativne.

Znak kota

V številnih besedilih se znak pogosto pojavlja skupaj z merilom kota, zlasti kota, ki se nahaja, ali kota vrtenja. V takem primeru znak pove, ali je kot v smeri urinega kazalca ali v nasprotni smeri urinega kazalca. Čeprav se lahko uporabljajo različne konvencije, je v matematiki običajno, da se koti v smeri urinega kazalca štejejo kot pozitivni, koti v smeri urinega kazalca pa kot negativni.

V treh dimenzijah je mogoče kotu vrtenja dodati tudi znak, če je os vrtenja usmerjena. Natančneje, desni zasuk okoli osi se običajno šteje kot pozitiven, medtem ko se levi zasuk šteje kot negativen.

Znak smeri

V aritmetiki in fiziki je običajno, da določene smeri označimo kot pozitivne ali negativne. Osnovni primer je številska premica, ki je običajno narisana s pozitivnimi števili na desni strani in negativnimi števili na levi:

Na kartezični ravnini sta smeri v desno in navzgor običajno pozitivni, pri čemer je smer v desno pozitivna smer x, smer navzgor pa pozitivna smer y.

Drugi pomeni

Poleg znaka realnega števila se beseda znak v matematiki in naravoslovju uporablja tudi na različne sorodne načine:

• V teoriji grafov je podpisani graf graf, v katerem je vsak rob označen s pozitivnim ali negativnim znakom.
• V fiziki je vsak električni naboj označen s pozitivnim ali negativnim znakom. Po splošnih pravilih je pozitivni naboj naboj z enakim predznakom, kot ga ima proton, negativni naboj pa je naboj z enakim predznakom, kot ga ima elektron.

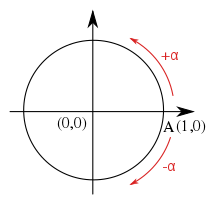
Če merimo od osi x, so koti na krogu enote pozitivni v smeri urinega kazalca in negativni v smeri urinega kazalca.


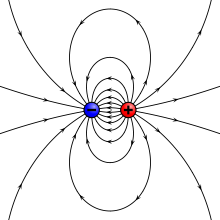
Električni naboj je lahko pozitiven ali negativen.

Išči po črki