Valj: definicija, lastnosti in formule za površino ter prostornino
Valj: jasna definicija, ključne lastnosti in praktične formule za izračun površine ter prostornine. Primeri in obrazci za enostaven izračun in razumevanje.
Valj je ena od najosnovnejših ukrivljenih geometrijskih oblik, katere površino tvorijo točke na določeni razdalji od dane premice, znane kot os valja. Obliko si lahko predstavljamo kot krožno prizmo. Tako površino kot trdno obliko, ki nastane v njej, lahko imenujemo valj. Površina in prostornina valja sta znani že od nekdaj.
V diferencialni geometriji je valj širše opredeljen kot vsaka pravilna površina, ki jo pokriva enoparametrska družina vzporednih premic. Valj, katerega presek je elipsa, parabola ali hiperbola, se imenuje eliptični valj, parabolični valj oziroma hiperbolični valj.
Osnovne lastnosti
- Os valja: premica, glede na katero so vse točke površine na enaki oddaljenosti (pri krožnem valju je to središčnica kroga).
- Generatrice (poševnice): vzporedne premice, ki tvorijo stransko površino valja. Njihova dolžina se imenuje generatrix ali poševna višina (pri pravem valju je enaka višini).
- Osnovni preseki: pri krožnem valju sta osnovi kroga, pri eliptičnem valju elipsi itd.; valj je v splošnem prizma z ukrivljenimi stranicami.
- Pravi (navpični) valj: generatrice so pravokotne na osnovno ploskev; pri krožnem pravem valju se govori o pravem krožnem valju.
- Poševni (nagnjeni) valj: generatrice niso pravokotne na osnovo; prostornina pri enakih osnovah in višini ostane enaka kot pri pravem valju.
Formule za krožni valj
Naj bo r polmer krožnice osnove, h pa višina (pravokotna razdalja med osnovama). Pri pravem krožnem valju veljajo naslednje formule:
- Ploskovna površina stranske (ukrivljene) površine: 2π r h
- Skupna površina (obe osnovi + stranska): 2π r (r + h) = 2π r^2 + 2π r h
- Prostornina: V = π r^2 h
Opombe:
- Pri poševnem krožnem valju je površina stranske plošče enaka obodu osnove pomnoženemu z dolžino generatrice l: 2π r · l. Skupna površina je torej 2π r^2 + 2π r l.
- Prostornina poševnega valja ostane enaka: V = (ploščina osnove) · (pravokotna višina) = π r^2 h, kjer je h pravokotna razdalja med osnovama, ne dolžina generatrice.
Geometrijska razlaga in razvitek
Razvitje (net) pravokornega krožnega valja razbije stransko površino na pravokotnik z dimenzijama obod osnove 2π r in višina h. Zato je površina tega pravokotnika 2π r h, kar vodi do formule za stransko površino.
Primer izračuna
Za krožni valj s polmerom r = 3 enote in višino h = 5 enot:
- Stranska površina = 2π · 3 · 5 = 30π ≈ 94,25 enot²
- Skupna površina = 2π · 3 · (3 + 5) = 48π ≈ 150,80 enot²
- Prostornina = π · 3² · 5 = 45π ≈ 141,37 enot³
Uporabe in dodatne opombe
- Valji so pogosti v tehničnih in naravoslovnih aplikacijah: rezervoarji, cevi, kolone, valjasti valji v mehaniki itd.
- V matematični analizi je valj pomemben primer pri obravnavi površin, integralov in pri proučevanju lastnosti ukrivljenih ploskev (npr. pri izračunu površine z uporabo parametričnih predstavitev).
- Tipične enote: površina v enotah² (npr. cm², m²), prostornina v enotah³ (npr. cm³, m³).
Valj torej povezuje preproste geometrijske pojme (krog, prizmo, ruled surface) in ima jasne, uporabne formule za izračune površine in prostornine, ki so uporabne v šoli in praksi.
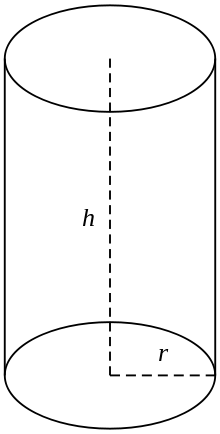
Pravokotni krožni valj
Pogosta uporaba
V splošni rabi valj pomeni končni presek pravokotnega krožnega valja, tj. valja, katerega generalne črte so pravokotne na osnove, njegova konca pa sta sklenjena v dve krožni površini, kot je prikazano na sliki (desno). Če ima valj polmer r in dolžino (višino) h, je njegova prostornina podana z:
V = πrh2
njegova površina pa je:
- površina vrha (πr2) +
- površina dna (πr2) +
- površino stranice (2πrh).
Zato je površina brez zgornjega ali spodnjega dela (stranska površina):
A = 2πrh.
Z zgornjim in spodnjim delom je površina:
A = 2πr 2+ 2πrh = 2πr(r + h).
Pri dani prostornini ima valj z najmanjšo površino h = 2r. Pri dani površini ima valj z največjo prostornino h = 2r, tj. valj se prilega kocki (višina = premer).
Zvezek
Pravokotni valj z višino h enot in osnovo s polmerom r enot, katerega koordinatni osi sta izbrani tako, da je izhodišče v središču osnove, višina pa se meri vzdolž pozitivne osi x. Ravninski odsek na razdalji x enot od začetka ima površino A(x) kvadratnih enot, kjer
A ( x ) = π r {\displaystyle2 A(x)=\pi r^{2}}
ali
A ( y ) = π r {\displaystyle2 A(y)=\pi r^{2}}
Element prostornine je desni valj z osnovno površino Awi kvadratnih enot in debelino Δxi enot. Če je torej V kubičnih enot prostornina desnega krožnega valja, po Riemannovih vsotah,
V o l u m e n a c i l i n d e r = lim | | Δ → |0 | ∑ i = n 1A ( w i ) Δ i x {\displaystyle \mathrm {Obsežnost\;od\;cilinder} =\lim _{||\Delta \to 0||}\sum _{i=1}^{n}A(w_{i})\Delta _{i}x}
= ∫0 h A ( y ) d2 y {\displaystyle =\int _{0}^{h}A(y)^{2}\,dy}
= ∫ 0h π r d2 y {\displaystyle =\int _{0}^{h}\pi r^{2}\,dy}
= π r h 2{\displaystyle =\pi \,r^{2}\,h\,}
S cilindričnimi koordinatami lahko prostornino izračunamo z integracijo nad
= ∫ 0h0 ∫ 2π ∫ 0r s d s d ϕ d z {\displaystyle =\int _{0}^{h}\int _{0}^{2\pi }\int _{0}^{r}s,\,ds\,d\phi \,dz}
= π r h 2{\displaystyle =\pi \,r^{2}\,h\,}
Cilindrični prerez
Cilindrični preseki so presečišča valjev z ravninami. Za desni krožni valj obstajajo štiri možnosti. Ravnina, ki je tangentna na valj, se stika z valjem v eni sami premici. Ravnina, ki jo premikamo vzporedno s seboj, bodisi ne seka valja bodisi ga seka v dveh vzporednih premicah. Vse druge ravnine sekajo valj v elipsi ali, če so pravokotne na os valja, v krogu.
Druge vrste valjev
Eliptični cilinder ali cilindroid je kvadrična površina z naslednjo enačbo v kartezičnih koordinatah:
( x a ) + 2( y b ) =21 . {\displaystyle \left({\frac {x}{a}}}\right)^{2}+\left({\frac {y}{b}}\right)^{2}=1.}
Ta enačba velja za eliptični valj, ki je posplošitev navadnega krožnega valja (a = b). Še bolj splošen je posplošen valj: presek je lahko poljubna krivulja.
Valj je degeneriran kvadrik, ker vsaj ena od koordinat (v tem primeru z) ne nastopa v enačbi.
Pri poševnem valju sta zgornja in spodnja površina med seboj pomaknjeni.
Obstajajo tudi druge, bolj nenavadne vrste valjev. To so namišljeni eliptični valji:
( x a ) + 2( y b ) =2 - 1{\displaystyle \left({\frac {x}{a}}}\right)^{2}+\left({\frac {y}{b}}\right)^{2}=-1}
hiperbolični valj:
( x a )2 - ( y b ) = 2{\displaystyle1 \left({\frac {x}{a}}\right)^{2}-\left({\frac {y}{b}}\right)^{2}=1}
in parabolični valj:
x + 2a 2y =0 . {\displaystyle x^{2}+2ay=0.\,}

Eliptični valj

V projektivni geometriji je valj preprosto stožec, katerega vrh je v neskončnosti, kar vizualno ustreza temu, da je valj v perspektivi videti kot stožec proti nebu.
Projektivna geometrija
V projektivni geometriji je valj preprosto stožec, katerega vrh je v neskončnosti.
To je uporabno pri definiciji degeneriranih stožcev, pri kateri je treba upoštevati cilindrične stožce.
Vprašanja in odgovori
V: Kaj je cilinder?
O: Valj je trirazsežna geometrijska oblika, katere površino tvorijo točke na določeni razdalji od dane premice, znane kot os valja. Lahko si ga predstavljamo kot krožno prizmo in tako površino kot trdno obliko, ki nastane v njej, lahko imenujemo valj.
V: Kako dolgo ljudje poznajo površino in prostornino valjev?
O: Površina in prostornina valjev sta znani že od nekdaj.
V: Kaj so eliptični, parabolični in hiperbolični valji?
O: Eliptični, parabolični in hiperbolični valji so valji, katerih presek je elipsa, parabola oziroma hiperbola.
V: Kako je valj definiran v diferencialni geometriji?
O: V diferencialni geometriji je valj širše definiran kot urejena površina, ki jo pokriva enoparametrska družina vzporednih premic.
V: Kaj pomeni, da je nekaj "urejeno"?
O: Če je nekaj "urejeno", to pomeni, da so na to tako ali drugače narisane ravne črte.
V: Ali obstaja samo ena vrsta valja?
O: Ne, obstaja veliko različnih vrst valjev, kot so eliptični, parabolični in hiperbolični valji, ki imajo različne preseke.
Iskati










