Zlato razmerje (φ): definicija, formula (1+√5)/2 in lastnosti
Če imamo eno število a in drugo manjše število b, razmerje med njima ugotovimo tako, da ju delimo. Njuno razmerje je a/b. Drugo razmerje dobimo tako, da seštejemo obe števili (a+b) in to delimo z večjim številom a; novo razmerje je (a+b)/a. Če sta ti dve razmerji enaki istemu številu, se to število imenuje zlato razmerje. Grška črka φ {\displaystyle \varphi } 
(phi) se običajno uporablja kot ime za zlato razmerje.
Definicija in osnovna enačba
Če označimo zlato razmerje z φ {\displaystyle \varphi } , potem iz pogoja a/b = (a+b)/a sledijo zveze, ki jih lahko zapišemo tudi tako. Če vzamemo primer, kjer je b = 1 in zato a = φ {\displaystyle \varphi } , je drugo razmerje (a+b)/a enako ( φ + 1 ) / φ {\displaystyle (\varphi +1)/\varphi } 
. Ker sta ti dve razmerji enaki, dobimo enačbo:
φ = {\displaystyle (\varphi +1)/\varphi }
Pomnožimo obe strani z φ in preuredimo, da dobimo kvadratno enačbo φ² = φ + 1. Rešitev te enačbe je:
φ = {\displaystyle {\frac {1+{\sqrt {5}}}{2}}}
{\displaystyle {\sqrt {5}}} 
pomeni pozitivno kvadratno korenino iz 5, torej število, ki ga, če ga pomnožimo samo s seboj, da rezultat 5: {\displaystyle {\sqrt {5}}\times {\sqrt {5}}=5} 
.
Numerična vrednost in lastnosti
Zlato razmerje je približno 1,6180339887..., torej
- iracionalno število: njegova decimalna predstava se nikoli ne konča in ne ponavlja; ni ga mogoče izraziti kot ulomek dveh celih števil; iracionalno število;
- kvadratna iracionalnost: φ je rešitev kvadratne enačbe φ² − φ − 1 = 0 in zato spada med kvadratne iracionalne številke;
- algebračna lastnost: φ² = φ + 1;
- recipročna lastnost: 1/φ = φ − 1 ≈ 0,6180339887… (torej je recipročna vrednost φ enaka φ zmanjšanemu za 1);
- kontinuiteta kot verižni ulomek: φ = 1 + 1/(1 + 1/(1 + 1/(…))) — neskončen verižni ulomek, kjer so vsi členi enaki 1;
- konjugat: druga rešitev kvadratne enačbe je ψ = (1 − √5)/2 ≈ −0,6180339887, pogosto imenovana zlata konjugata.
Povezava s Fibonaccijevim zaporedjem
Razmerje zaporednih členov Fibonaccijevega zaporedja F_{n+1}/F_n konvergira proti φ, ko n raste proti neskončnosti. Zaradi tega se φ pogosto pojavlja v lastnostih zaporedja Fibonaccijevih števil in v izpeljavah Binetove formule.
Uporabe in pojavnost
Zlato razmerje se pojavlja v geometriji (npr. zlati pravokotnik, pentagram, enakomerni petkotnik), v naravnih vzorcih (razporeditev listov na steblu, ramificiranje), v umetnosti in arhitekturi (razmerja, ki jih nekateri avtorji povezujejo z estetsko privlačnostjo) ter v računalništvu in teoriji števil. Pomembno je razumeti, da so trditve o »čarobnosti« zlatega razmerja pogosto posplošene — številka ima zanimive matematične lastnosti in se pogosto pojavi v praktičnih modelih, vendar ni univerzalni kriterij lepote.
Kaj si zapomniti
- Definicija: φ je tisto pozitivno število, pri katerem je razmerje večjega dela do manjšega enako razmerju celote do večjega dela.
- Formula: φ = {\displaystyle {\frac {1+{\sqrt {5}}}{2}}}
. - Lastnosti: φ² = φ + 1 in 1/φ = φ − 1.
Zlati pravokotnik
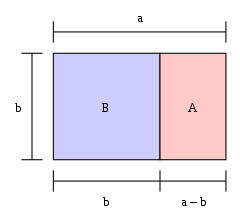
Če je dolžina pravokotnika, deljena z njegovo širino, enaka zlatemu rezu, je pravokotnik "zlati pravokotnik". Če z enega konca zlatega pravokotnika odrežemo kvadrat, je drugi konec nov zlati pravokotnik. Na sliki je veliki pravokotnik (modri in rožnati skupaj) zlati pravokotnik, ker je a / b = φ {\displaystyle a/b=\varphi } 
. Modri del (B) je kvadrat. Rožnati del sam po sebi (A) je še en zlati pravokotnik, ker je b / ( a - b ) = φ {\displaystyle b/(a-b)=\varphi } 
. Veliki pravokotnik in rožnati pravokotnik imata enako obliko, vendar je rožnati pravokotnik manjši in obrnjen.
Veliki pravokotnik BA je zlati pravokotnik; to pomeni, da je razmerje b:a 1: φ {\displaystyle \varphi } . Če za vsak tak pravokotnik in samo za pravokotnike s tem posebnim razmerjem odstranimo kvadrat B, ostane A, ki je še en zlati pravokotnik; to je pravokotnik z enakimi razmerji kot prvotni pravokotnik.
Fibonaccijeva števila
Fibonaccijeva števila so seznam števil. Naslednje število na seznamu lahko najdemo tako, da seštejemo zadnji dve številki. Če število na seznamu delimo s številom, ki je bilo pred njim, se to razmerje vedno bolj približuje zlatemu rezu.
| Fibonaccijevo število | deljeno s tistim pred | razmerje |
| 1 | ||
| 1 | 1/1 | = 1.0000 |
| 2 | 2/1 | = 2.0000 |
| 3 | 3/2 | = 1.5000 |
| 5 | 5/3 | = 1.6667 |
| 8 | 8/5 | = 1.6000 |
| 13 | 13/8 | = 1.6250 |
| 21 | 21/13 | = 1.6154... |
| 34 | 34/21 | = 1.6190... |
| 55 | 55/34 | = 1.6177... |
| 89 | 89/55 | = 1.6182... |
| ... | ... | ... |
| φ {\displaystyle \varphi } | = 1.6180... |
Zlato razmerje v naravi
V naravi se zlato razmerje pogosto uporablja za razporeditev listov ali cvetov. Ti uporabljajo zlati kot, ki znaša približno 137,5 stopinj. Listje ali cvetje, razporejeno pod tem kotom, najbolje izkorišča sončno svetlobo.
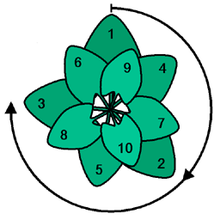
Z uporabo zlatega kota boste optimalno izkoristili sončno svetlobo. To je pogled z vrha.
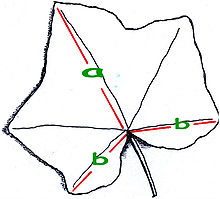
List navadnega bršljana, ki kaže zlato razmerje
Vprašanja in odgovori
V: Kakšno je razmerje dveh števil?
O: Razmerje dveh števil ugotovimo tako, da ju delimo, zato je razmerje a/b.
V: Kako lahko najdemo drugo razmerje?
O: Drugo razmerje lahko najdemo tako, da seštejemo obe števili in nato to vsoto delimo z večjim številom a. To novo razmerje bi bilo (a+b)/a.
V: Kako imenujemo primer, ko sta ti dve razmerji enaki drug drugemu?
O: Ko sta ti dve razmerji enaki drug drugemu, se to imenuje zlato razmerje. Običajno ga predstavljamo z grško črko צ ali phi.
V: Če je b = 1 in a/b = צ , kaj to pomeni za a?
O: Če je b = 1 in a/b = צ , to pomeni, da je tudi a = צ .
V: Kako lahko to število zapišemo?
O: To število lahko zapišemo tako: צ = 1 + 5 / 2 = 1,618 ...
V: Kaj pomeni, če od tega števila odštejemo 1 ali z njim delimo 1?
O: Če od njega odšteješ 1 ali ga deliš z 1, boš dobil nazaj isto število - z drugimi besedami, obe številki bosta enaki zlatemu rezu.
V: Ali je zlato razmerje iracionalno število?
O: Da, zlato razmerje je iracionalno število, kar pomeni, da če ga nekdo poskuša zapisati, ne bo nikoli konca in vzorca - začne se samo z nečim, kot je "1,6180339887 ...".
