AlegsaOnline.com

Gravitacijski pospešek g – definicija, enota in vrednost

Gravitacijski pospešek g: definicija, SI enota m/s2, standardna vrednost 9,80665 m/s2 in kako lokacija na Zemlji vpliva na pospešek pri prostem padu

Avtor: Leandro Alegsa

25-08-2025

Pospešek, ki ga dobi predmet zaradi gravitacijske sile, imenujemo gravitacijski pospešek. Njegova enota SI je m/s². Pospešek zaradi težnosti je vektor, kar pomeni, da ima velikost in smer — usmerjen je proti središču Zemlje. Pospešek zaradi težnosti na površini Zemlje označujemo s črko g. Njegova standardna vrednost je 9,80665 m/s² (32,1740 ft/s²). Vendar se dejanski pospešek telesa pri prostem padu spreminja glede na lokacijo.

Osnovna formula in povezava s težnostjo

Newtonov zakon univerzalne gravitacije pove, da je velikost gravitacijskega pospeška na razdalji r od središča mase M dana z izrazom:

g(r) = G·M / r²,

kjer je G gravitacijska konstanta. Za Zemljo to pomeni, da g pada s povečevanjem višine nad površjem. Za majhne višine h nad površjem je približek

g(h) ≈ g₀ · (1 − 2h / R),

kjer je R polmer Zemlje in g₀ vrednost pri površju. Poleg tega Zemljina rotacija povzroča centrifugalno pospeševanje, ki nekoliko zmanjša efektivni g, predvsem bližje ekvatorju.

Prostorska spreminjanja in tipične vrednosti

Na Zemlji se vrednost g spreminja z zemljepisno širino, višino in lokalno gostoto podlage. Tipične vrednosti se gibljejo približno od 9,78 m/s² na ekvatorju do približno 9,83 m/s² na polih. Lokalna geologija (gostejše ali redkejše kamnine) lahko povzroči dodatne manjše odstopanja, ki jih merimo z gravimetri.

Pomen v fiziki in vsakdanji uporabi

Gravitacijski pospešek se uporablja za izračun teže telesa: F = m·g, kjer je m masa telesa. Poznavanje lokalne vrednosti g je pomembno v inženirstvu, balistiki, meteorologiji in pri kalibraciji merilnih naprav.

Merenje

Gravitacijski pospešek se lahko izmeri na več načinov: z izpusti v prostem padu, z meritvami nihanja preprostih in sestavljenih nihal ali z moderno opremo, kot so seizmični gravimetri in atomski gravimetri, ki merijo spremembe gravitacijskega polja z visoko natančnostjo.

Gravitacijski pospešek na drugih nebesnih telesih

Na drugih telesih so vrednosti g precej nižje ali višje glede na maso in velikost telesa — na primer na Luni je g približno 1,62 m/s², na Marsu približno 3,71 m/s². To vpliva na gibanje predmetov, višino skokov in tehtanje na teh telesih.

Zakaj težji predmeti ne padajo hitreje kot lažji predmeti

Isaac Newton je ugotovil, da je rezultanta sile enaka masi, pomnoženi s pospeškom, ali v simbolih: F = m a {\displaystyle F=ma} $F=ma$ . To lahko preuredimo in dobimo a = F m {\displaystyle a={\frac {F}{m}}}} } $a={\frac {F}{m}}\$ . Večja kot je masa padajočega predmeta, večja je sila gravitacijske privlačnosti, ki ga vleče proti Zemlji. V zgornji enačbi je to F {\displaystyle F} . Vendar pa je število krat, ko se sila poveča ali zmanjša, enako številu krat, ko se masa poveča ali zmanjša, pri čemer razmerje ostane konstantno. V vsakem primeru se F m {\displaystyle {\frac {F}{m}}} ${\frac {F}{m}}\$ izniči do enakomernega pospeška približno 9,8 m/s² . To pomeni, da ne glede na maso vsa prosto padajoča telesa pospešujejo z enako hitrostjo.

Oglejte si naslednje primere:

a = 49 N 5 k g = 9,8 N / k g = 9,8 m / s 2 {\displaystyle a={\frac {49\,\mathrm {N} }{5\,\mathrm {kg} }}\ =9,8\,\mathrm {N/kg} =9,8\,\mathrm {m/s^{2}} } $a={\frac {49\,\mathrm {N} }{5\,\mathrm {kg} }}\ =9.8\,\mathrm {N/kg} =9.8\,\mathrm {m/s^{2}}$

a = 147 N 15 k g = 9,8 N / k g = 9,8 m / s 2 {\displaystyle a={\frac {147\,\mathrm {N} }{15\,\mathrm {kg} }}\ =9,8\,\mathrm {N/kg} =9,8\,\mathrm {m/s^{2}} } $a={\frac {147\,\mathrm {N} }{15\,\mathrm {kg} }}\ =9.8\,\mathrm {N/kg} =9.8\,\mathrm {m/s^{2}}$

Površinski pospešek

Glede na lokacijo pade predmet na površini Zemlje s pospeškom med 9,76 in 9,83 m/s² (32,0 in 32,3 ft/s² ).

Zemlja ni ravno okrogla. Podobna je "zmečkani" krogli, pri kateri je polmer na ekvatorju nekoliko večji od polmera na polih. Zaradi tega se gravitacijski pospešek na polih nekoliko poveča (ker smo blizu središča Zemlje in je gravitacijska sila odvisna od razdalje), na ekvatorju pa se nekoliko zmanjša. Prav tako je zaradi centripetalnega pospeška gravitacijski pospešek na ekvatorju nekoliko manjši kot na polih. Spremembe v gostoti kamnin pod tlemi ali prisotnost gora v bližini lahko nekoliko vplivajo na gravitacijski pospešek.

Nadmorska višina

Pospešek predmeta se spreminja z višino. Sprememba težnega pospeška z oddaljenostjo od središča Zemlje poteka po zakonu obratnega kvadrata. To pomeni, da je gravitacijski pospešek obratno sorazmeren kvadratu razdalje od središča Zemlje. Ko se razdalja podvoji, se gravitacijski pospešek zmanjša za faktor 4. Ko se razdalja potroji, se gravitacijski pospešek zmanjša za faktor 9 in tako naprej.

gravitacijski pospešek ∝ 1 razdalja 2 {\displaystyle {\mbox{gravitacijski pospešek}} \\propto \ {\frac {1}{{\mbox{razdalja}}^{2}}}} } ${\mbox{gravitational acceleration}}\ \propto \ {\frac {1}{{\mbox{distance}}^{2}}}\$

gravitacijski pospešek × razdalja 2 = k {\displaystyle {\mbox{gravitacijski pospešek}} \\krat {{\mbox{razdalja}}}^{2}}\ ={k}} ${\mbox{gravitational acceleration}}\ \times {{\mbox{distance}}^{2}}\ ={k}$

Na površju Zemlje je pospešek zaradi težnosti približno 9,8 m/s² (32 ft/s² ). Povprečna razdalja do središča Zemlje je 6.371 km (3.959 milj).

k = 9,8 × 6371 2 {\displaystyle {k}={\mbox{9,8}} \krat {{\mbox{6371}}^{2}}} ${k}={\mbox{9.8}}\ \times {{\mbox{6371}}^{2}}$

Z uporabo konstante k {\displaystyle k} lahko izračunamo gravitacijski pospešek na določeni višini.

gravitacijski pospešek = k razdalja 2 {\displaystyle {\mbox{gravitacijski pospešek}} ={\frac {k}{{\mbox{razdalja}}}^{2}}}}}\ } ${\mbox{gravitational acceleration}}\ ={\frac {k}{{\mbox{distance}}^{2}}}\$

Primer: Poiščite težnostni pospešek na višini 1.000 km nad Zemljinim površjem.

6371 + 1000 = 7371 {\displaystyle 6371+1000=7371} $6371+1000=7371$

∴ Oddaljenost od središča Zemlje je 7.371 km.

gravitacijski pospešek = 9,8 × 6371 2 7371 2 ≈ 7,3 {\displaystyle {\mbox{gravitacijski pospešek}} ={\frac {{\mbox{9,8}} \\krat {{\mbox{6371}}^{2}}}}{{\mbox{7371}}^{2}}}} \\aprox 7,3} ${\mbox{gravitational acceleration}}\ ={\frac {{\mbox{9.8}}\ \times {{\mbox{6371}}^{2}}}{{\mbox{7371}}^{2}}}\ \approx 7.3$

∴ Pospešek zaradi težnosti 1.000 km (620 milj) nad površjem Zemlje je 7,3 m/s² (24 ft/s² ).

Gravitacijski pospešek na Kármánovi črti, meji med Zemljinim ozračjem in vesoljem, ki leži na višini 100 km, je le približno 3 % manjši kot na ravni morja.

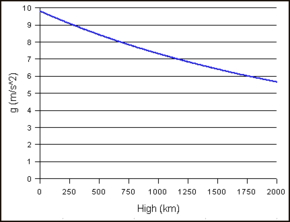
Sprememba gravitacijskega pospeška z višino predmeta

Vprašanja in odgovori

V: Kaj je gravitacijski pospešek?

O: Pospešek zaradi gravitacije je pospešek, ki ga dobi predmet zaradi gravitacijske sile.

V: Kakšna je enota SI za gravitacijski pospešek?

O: Enota SI za gravitacijski pospešek je m/s2.

V: Ali je gravitacijski pospešek skalar ali vektor?

O: Gravitacijski pospešek je vektor, ker ima velikost in smer.

V: Kakšen simbol se uporablja za predstavitev težnega pospeška na površju Zemlje?

O: Simbol, ki se uporablja za predstavitev težnega pospeška na površini Zemlje, je g.

V: Katera je standardna vrednost težnega pospeška na površju Zemlje?

O: Standardna vrednost težnega pospeška na površju Zemlje je 9,80665 m/s2 (32,1740 ft/s2).

V: Ali se dejanski pospešek telesa pri prostem padu spreminja glede na lokacijo?

O: Da, dejanski pospešek telesa pri prostem padu se spreminja glede na lokacijo.

V: Kakšna je definicija težnostnega pospeška?

O: Pospešek zaradi težnosti je pospešek, ki ga dobi predmet zaradi sile težnosti, in se izraža s črko g s standardno vrednostjo 9,80665 m/s2 na površju Zemlje, medtem ko se dejanski pospešek lahko spreminja glede na lokacijo.